2. 中国空气动力研究与发展中心 计算空气动力研究所,四川 绵阳 621000
2. Computational Aerodynamics Institutes, China Aerodynamics Research and Development Center, Mianyang 621000, China
高超声速冲压发动机技术的发展,对超声速变形流道的设计提出了新的需求,例如转弯变形流道是连接进气道与燃烧室的重要部件。然而,由于其内部为超声速气流,转弯和变形的型面必须避免激波的生成,否则将大大增加流动损失,降低发动机性能。这类流道通常需要实现三维空间复杂曲面的均匀过渡[1, 2]。但是目前三维流场的反问题仍然是国际上学术领域的前沿和难点。因此在截面变形流道,绕中心线转弯流道以及兼具变形和转弯约束流道的设计中,全三维流场的设计方法就显得尤为重要[3]。若能完成三维超声速气动设计方法的创新、研究和突破,将进一步推动高超声速三维进气道、隔离段、尾喷管及燃烧室等的设计和应用。
国内外对三维超声速复杂气动外形的设计研究有着悠久的历史。Murthy等[4]采用变分法对三维喷管的设计问题展开了研究。Damodaran等[5, 6]采用CFD结合模拟退火的优化方法对三维圆转椭圆喷管的过渡型面进行了一些优化分析。在冲压发动机进排气系统的设计领域,能够实现三维超声速气动设计且应用较为成熟的方法主要包括流线追踪技术和密切理论。
Moelder等[7, 8]结合轴对称内压缩流场、流线追踪技术和曲面放样,提出了高超声速方转椭圆进气道(REST)的设计方法[9]。这种构型即考虑到了方形入口进气道便于多模块集成,又兼顾了与圆形燃烧室的对接,是进气道设计方法上一次很大的创新[10, 11]。流线追踪技术能够截取流场获得进气道构型并继承基准流场的高性能,但是该方法对基准流场的设计具有一定的依赖性[12, 13],并且流线的几何融合对于流场本身的特性考虑较少,如果控制得不好,就会出现流向涡、激波诱导分离等,从而造成压力损失和反压前传。
密切理论、密切轴对称理论自Sobieczky[14, 15]提出以来,广泛应用于内外流压缩流场的组织,如乘波体飞行器、高超声速进气道等。密切锥乘波体设计方法[16]、双密切轴对称近似设计方法[17]、三维变截面尾喷管设计方法[18]等不断出现。密切理论结合特征线方法,是进行三维反问题求解的重要手段,其基本原则是:在保证小的横向压力梯度条件下,采用“切片”设计思想拼接设计流场。其思想的关键在于“切片”设计及避免横向流动。因此在一定几何约束条件下,密切理论难以直接应用于强三维流场的精细组织。
预设边界压力分布求解几何形状是一种新的思路。如果能够预设压力分布,反求形成该压力分布的曲面,就能有效控制流场的压缩过程,从而避免压缩波汇聚成激波,防止壁面逆压梯度过大引起的分离[19]。近些年来,国内许多单位针对边界反问题提出了相应的解法。2013年,南京航空航天大学的全志斌等设计了壁面压力分布可控的单边膨胀喷管[20]。2015年,赵玉新等提出一种三维超声速流动的压力反问题,并构造了边界反Riemann求解器[21],实现了入口为矩形、椭圆形、扇环形流管的三维设计;2015年,刘红阳根据轴线马赫数分布提出了特征线追踪方法[22]。2016年厦门大学的李怡庆等设计了壁面压力分布可控的高超声速进气道[23]。
为了进一步探索三维超声速流线压力反问题的求解方法,本文通过分析三维特征线方法[24~29],提出三维超声速压力反问题的双特征线解法,通过壁面坐标与压力对应的映射函数的数值求解,进行三维超声速流场的设计[30]。本文设计了入口为矩形和三角形的超声速喷管;通过调控壁面压力分布,设计了均匀膨胀的轴对称喷管。采用商用软件Fluent对设计的喷管进行数值模拟,并将模拟结果与设计结果进行对比。
2 双特征线算法 2.1 特征方程及相容方程三维、定常、无粘、可压、等熵流动的控制方程为
| $\rho u{u_x} + \rho v{u_y} + \rho w{u_z} + {p_x} = 0$ | (1) |
| $\rho u{v_x} + \rho v{v_y} + \rho w{v_z} + {p_y} = 0$ | (2) |
| $\rho u{w_x} + \rho v{w_y} + \rho w{w_z} + {p_z} = 0$ | (3) |
| $u{p_x} + v{p_y} + w{p_z} + \rho {a^2}\left( {{u_x} + {v_y} + {w_z}} \right) = 0$ | (4) |
| $u{p_{{\rm{T}}x}} + v{p_{{\rm{T}}y}} + w{p_{{\rm{T}}z}} = 0$ | (5) |
| $u{H_x} + v{H_y} + w{H_z} = 0$ | (6) |
| $a = a\left( {p, P, H} \right)$ | (7) |
式中u,v,w为x,y,z方向的速度,p为静压,ρ为密度,a为声速,p为总压,H为总焓,下标x,y,z表示对x,y,z坐标方向的方向导数。这些方程可以写成如下所示的特征方程和相容方程。
特征方程
| $ {\rm{d}}x/{\rm{d}}t = u, \;\;\;{\rm{d}}y/{\rm{d}}t = v, \;\;\;{\rm{d}}z/{\rm{d}}t = w $ | (8) |
| $ \begin{array}{*{20}{l}} {\left[ {{u^2} - \left( {{V^2} - {a^2}} \right)} \right]{{\left( {{\rm{d}}x} \right)}^2} + \left[ {{v^2} - \left( {{V^2} - {a^2}} \right)} \right]{{\left( {{\rm{d}}y} \right)}^2} + }\\ {\left[ {{w^2} - \left( {{V^2} - {a^2}} \right)} \right]{{\left( {{\rm{d}}z} \right)}^2} + 2uv\left( {{\rm{d}}x} \right)\left( {{\rm{d}}y} \right) + }\\ {2uw\left( {{\rm{d}}x} \right)\left( {{\rm{d}}z} \right) + 2vw\left( {{\rm{d}}y} \right)\left( {{\rm{d}}z} \right) = 0} \end{array} $ | (9) |
相容方程
| $ \rho u{u_{\rm{t}}} + \rho v{v_{\rm{t}}} + \rho w{w_{\rm{t}}} + {p_{\rm{t}}} = 0 $ | (10) |
| $ {p_{\rm{t}}} - {a^2}{\rho _{\rm{t}}} = 0 $ | (11) |
| $ \begin{array}{*{20}{l}} {\rho a{n_x}{u_{\rm{t}}} + \rho a{n_y}{v_{\rm{t}}} + \rho a{n_z}{w_{\rm{t}}} - {p_{\rm{t}}} + \rho {a^2} \times }\\ {[\left( {n_x^2 - 1} \right){u_x} + \left( {n_y^2 - 1} \right){v_y} + \left( {n_z^2 - 1} \right){w_z} + }\\ {\left( {{u_y} + {v_x}} \right){n_x}{n_y} + \left( {{u_z} + {w_x}} \right){n_x}{n_z} + \left( {{v_z} + {w_y}} \right){n_y}{n_z}] = 0} \end{array} $ | (12) |
其中
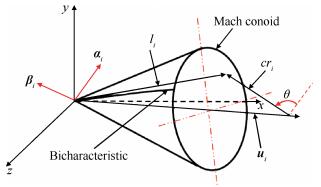
本文采用的数值积分网格为Butler提出的五面体双特征线网格,其中的双特征线采用了如图 1所示的参数化表示法。
|
Fig. 1 Bicharacteristic parameterization |
图中矢量ui,αi和βi为一组正交向量,q为速度的大小,θ是规定的双特征线的参数角,c为马赫锥与微团轨迹垂直的平面上的扩张速度,ri表示该横截面内的半径方向。由于马赫锥在当地是一个直锥,它的轴线与速度矢量相切,圆锥底面是一个平面,该平面平行于矢量αi和βi组成的平面,因此双特征线可以用下式参数方程表示
| $ {\rm{d}}{x_i} = \left( {{\mathit{\boldsymbol{u}}_i} + c{r_i}} \right){\rm{d}}t = \left( {{\mathit{\boldsymbol{u}}_i} + c{\mathit{\boldsymbol{\alpha }}_i}{\rm{cos}}\theta + c{\mathit{\boldsymbol{\beta }}_i}{\rm{sin}}\theta } \right){\rm{d}}t $ | (13) |
其中参数c由下式确定
| $ c = {\left( {{a^2}{q^2}/\left( {{q^2} - {a^2}} \right)} \right)^{1/2}} $ | (14) |
式中a为当地声速。
通过双特征线的参数化,沿双特征线的相容方程(12)可转换为下式
| $ \begin{array}{*{20}{l}} {{{\rm{d}}_l}p + \rho c\left( {{\mathit{\boldsymbol{\alpha }}_i}{\rm{cos}}\theta + {\mathit{\boldsymbol{\beta }}_i}{\rm{sin}}\theta } \right){{\rm{d}}_l}{\mathit{\boldsymbol{u}}_i} = - \rho {c^2} \cdot }\\ {\left( {{\mathit{\boldsymbol{\alpha }}_i}{\rm{sin}}\theta - {\mathit{\boldsymbol{\beta }}_i}{\rm{cos}}\theta } \right) \cdot \left( {{\mathit{\boldsymbol{\alpha }}_j}{\rm{sin}}\theta - {\mathit{\boldsymbol{\beta }}_j}{\rm{cos}}\theta } \right)\left( {\partial {\mathit{\boldsymbol{u}}_i}/\partial {x_j}} \right){\rm{d}}t}\\ {\theta = 0, {\rm{ \mathsf{ π} }}/2, {\rm{ \mathsf{ π} }}, {\rm{}}3{\rm{ \mathsf{ π} }}/2{\rm{}}} \end{array} $ | (15) |
式中dlp定义为压力沿着双特征线曲线切线方向的方向导数。
此外,Buler导出了一个在微团轨迹上能够成立的非特征线关系式
| $ {{\rm{d}}_u}p = - \rho {c^2}\left( {{\mathit{\boldsymbol{\alpha }}_i}{\mathit{\boldsymbol{\alpha }}_j} + {\mathit{\boldsymbol{\beta }}_i}{\mathit{\boldsymbol{\beta }}_j}} \right)\left( {\partial {\mathit{\boldsymbol{u}}_i}/\partial {x_i}} \right){\rm{d}}t $ | (16) |
式中dup定义为压力沿着流线切线的方向导数。
四个双特征线相容性方程(15)可以用θ=0,π/2,π,3π/2写出。采用有限差分法离散这四个方程与式(16)。这五个有限差分方程通过线性组合,获得三个相互独立的方程,同时也消除了解点上的交叉导数[25]。这三个独立的方程加上在微团轨迹上成立的两个相容性方程组成一个方程组,用改进的欧拉预估-校正法进行求解。
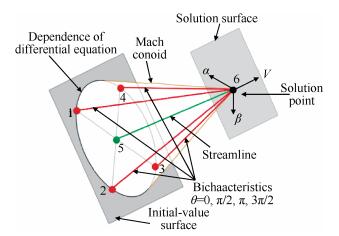
通过双特征线的参数化、流线上的非特征线关系式以及差分方程数值叠加消除交叉导数,从而获得不越出解点依赖域(满足CFL稳定性准则)而达到二阶精度的格式,如图 2所示。图中5点为微团轨迹与初值面的交点,6点为解点,其位置由5点向前延伸微团轨迹来确定。随后四条间隔相同的双特征线从6点向后延伸,与初值面在1,2,3和4点处相交。1~5点上的流动参数由拟合了5点和八个相邻点的双变量内插多项式来确定。
|
Fig. 2 Pentahedral line network |
对于超声速无粘情况下的固体边界,流体必须与边界相切,并且边界流线和实体壁面相互重合。流动相切条件如下式所示
| $ {n_i}{\mathit{\boldsymbol{u}}_i} = 0 $ | (17) |
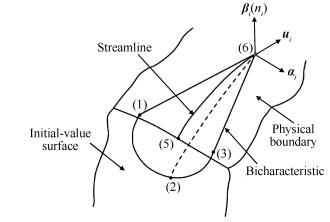
式中ni是单位边界外法线。用流线相切的条件代替四条双特征线之一的相容性方程,内点单元即可修改为边界单元,而剩下的3条双特征线的方向也随之被确定,如图 3所示,θ=0和π对应的双特征线在壁面的切平面内,θ=π/2对应的双特征线在流场内部。
|
Fig. 3 Unit progress of physical boundary |
沿流动方向进行空间推进时,逐个截面间的距离必须调整到使网格上所有点均满足CFL稳定性准则。可允许的步长大小由下式给出:
| $ {\rm{\Delta }}x = [{u^2}/\left( {cq} \right)\left] \times \right[1 - \left( {c/q} \right)\left( {{q^2}/{u^2} - 1{)^{1/2}}} \right]{R_{{\rm{min}}}} $ | (18) |
其中Rmin以流线与初值面的交点为圆心,作有限差分网格凸包的内接圆的半径。
3 三维压力反问题求解器 3.1 双特征线求解技术本文基于双特征线的概念以及通过对Butler方法的分析,发现在壁面压力有物理解的情况下,一个相同的壁面压力对应着无穷多的壁面位置。即预设三维流线下游未知点的压力值,存在多个流动方向满足该压力条件,说明该问题的解不唯一,是非适定的。
对于二维的压力反问题,给定一个预设的压力值,壁面的流线微元通过调整流动方向,逼近给定的压力值。这相当于有一根垂直于平面向外的轴,流线微元绕着此轴旋转,旋转的角度与压力存在一一映射关系,如图 4所示。对于超声速无粘流动,流线和壁面可以相互替换,因此,壁面绕着轴旋转,就是将当地的膨胀/压缩方向限制在旋转轴作为法线的平面上。当流线膨胀/压缩方向严格地限定在旋转轴作为法线的平面上,且旋转轴始终固定,此时的压力反问题为二维压力反问题。
|
Fig. 4 Unit progress of two-dimensional pressure inverse problem |
为了确保三维压力反问题解的唯一性,本文提出并验证了在限定壁面膨胀/压缩方向时,仍存在壁面压力与坐标的一一映射关系,如下式所示
| $ {P_{6i}} = f\left( {{\theta _i}} \right) $ | (19) |
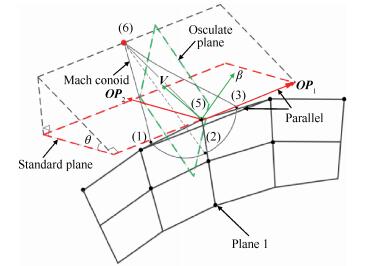
通过构造该函数关系,并进行数值求解,实现了三维压力反问题的双特征线求解算法(Three-dimensional supersonic pressure inverse problem using MOC,iMOC-3D),如图 5所示。旋转轴为向量OP1,向量OP1是与5点左右两点的连线相互平行的单位向量,因此旋转是当地相关而不是全局不变。同时,绕着旋转轴旋转的并非是流线微元L56,而是一个基准平面,因为5点的三个流动速度分量和向量OP1的三个坐标分量不相关(二维情况它们垂直相关),因此在进行预估-校正求解方程组时,流线微元L56不能保证在以向量OP1为法线的平面内。
|
Fig. 5 Unit progress of three-dimensional pressure inverse problem[30] |
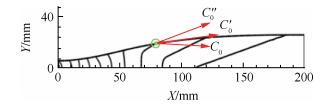
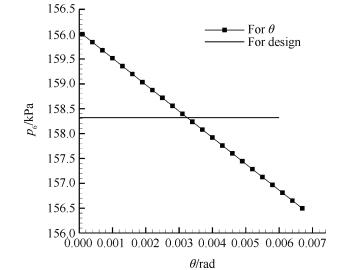
具体算法为:在5点建立基准面,该基准面由向量OP1和向量OP2共同构成,OP2为向量(1,0,0)。直线56为流线微元。密切面由矢量V和上游的βi共同构成,V为5点和6点的平均速度矢量,βi为流动相切条件中的ni。流线56为由密切面和基准面旋转θ角的平面相贯获得,旋转角度的正方向满足旋转轴为OP1的右手定则。图 6为其中一个单元过程6点压力和θ值的单调关系。
|
Fig. 6 Relationship between pressure and θ at point 6 |
可见,p6会随着θ的增大而减小,反之亦然。通过给定6点压力的设计值,反求对应的θ值,从而获得6点的三维坐标,这就是三维压力反问题。
3.2 求解器的精度验证文献[30]中采用Prandtl-Meyer膨胀波的理论解对iMOC-3D的设计精度进行了评估,其中压力、马赫数与精确解的相对误差为8×10-4,8.6×10-4,但该文献仅考虑了膨胀流动过程的验证。因此本小节采用基准Busemann流场评估iMOC-3D等熵压缩过程的设计精度。
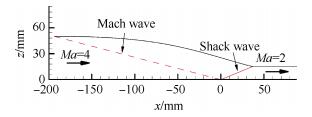
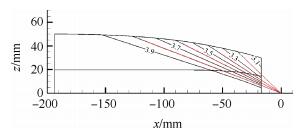
基准Busemann进气道的构型如图 7所示,马赫数4的无粘气流,经过型面产生一系列等熵压缩的马赫波,这些马赫波均汇聚于轴线上的一点(以该点作为坐标系原点),最后气流经过马赫波汇聚形成的锥形激波,产生方向与来流一致,马赫数为2的流场。
|
Fig. 7 Busemann inlet |
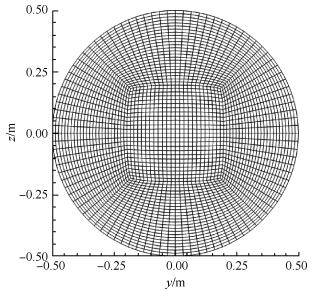
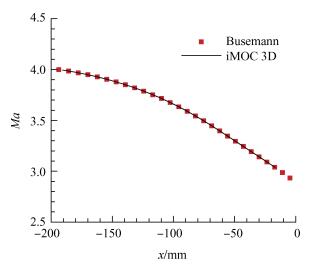
采用该流场的壁面压力分布作为iMOC-3D的输入项。初始截面如图 8所示,每个block网格量为25×25,该截面的尺寸和位置均同图 7所示进气道的进口截面一致,即x=-193.649mm,r=50mm。所得结果如图 9所示,其中黑色马赫数等值线为iMOC-3D解,红色直线为马赫线的延长线,可以看出,马赫数等值线的延长线汇聚于原点。图 10为壁面流线的马赫数分布,其中黑线为iMOC-3D解,红点为Busemann进气道的理论解,各参数的最大相对误差见表 1。
|
Fig. 8 O-block Mesh in initial-value surface |
|
Fig. 9 Comparison solutions between Busemann flow and Bicharacteristics method |
|
Fig. 10 Comparison Mach number between Busemann flow and Bicharacteristics method |
|
|
Table 1 Error study for Busemann flow |
为了验证iMOC-3D求解方法的有效性和可控性,设计了异形进口的超声速喷管;通过压力分布的设计来控制喷管内部流场。喷管入口均为马赫数为2.45的平行均匀流,静压为160kPa,静温为3149.67K,密度为0.177kg/m3,比热比1.25。在壁面上调用压力反问题求解器,内部流场采用双特征线方法进行计算。
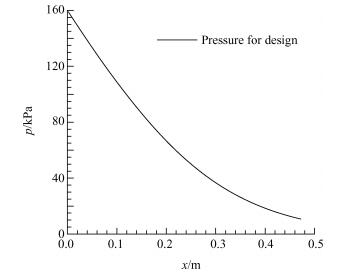
4.1 异型入口的超声速喷管若预设的壁面压力变化过于剧烈,容易出现强压缩波,因此本小节采用Butler方法计算了一个超椭圆喷管,将其壁面压力分布作为一个较为合理的壁面压力分布,如图 11所示。其中超椭圆的壁面函数为(y/y0)2+(z/z0)2=1,其中z0=y0=0.1+0.4×x2。
|
Fig. 11 Given pressure distribution |
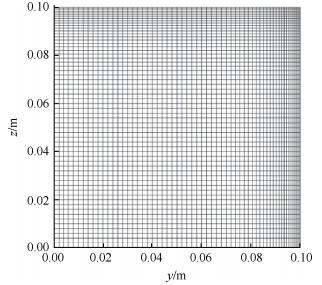
考虑空间的对称性,为了减少计算量,仅计算全尺寸的1/4,图 12为进口截面第一象限的网格划分,图 13为喷管第一象限的等轴视图。进口截面的网格量为61×61,为了更细致地捕捉角区处的流动,在角区进行加密,该算例采用空间步进的方式沿x方向步进180次,获得的步进距离共为0.34401m,在主频为2.6GHz的PC上运行时间需要30s。从沿程壁面的形变来看,由于不同位置的膨胀效率不同,为了获得相等的周向压力,使得几何构型的变化呈现为三维空间复杂曲面的变形。
|
Fig. 12 Inlet mesh in first quadrant |

|
Fig. 13 Isometric view of the rectangular nozzle |
图 14为y=0处截面的马赫数等值线,图中可以看出,喷管内部膨胀较为均匀,马赫线型较为平滑。

|
Fig. 14 Mach number contour line in y=0 section |
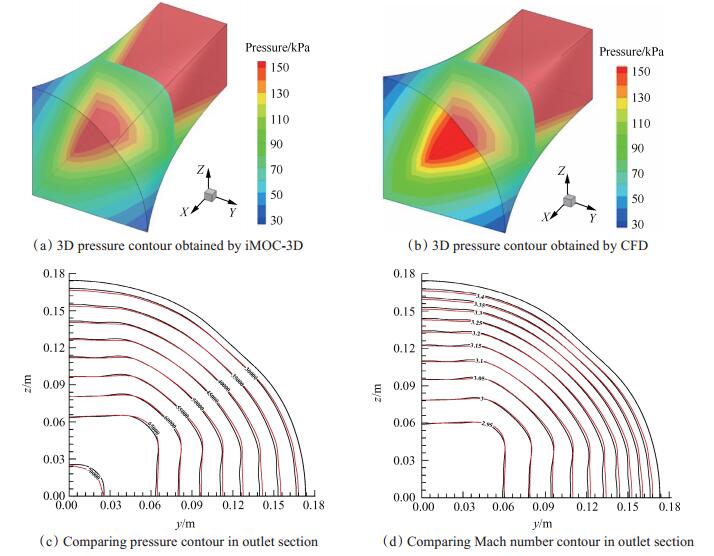
为验证设计方法的可靠性,将图 13所示的网格导入CFD进行数值模拟,模拟的控制方程采用Euler方程,结果如图 15(a)~(d)所示,分别为iMOC-3D和CFD计算的三维压力云图以及出口截面的压力等值线图、马赫数等值线图,其中黑色为iMOC-3D设计流场的等值线,红色为CFD计算得到的等值线。图中可以直观地看出不同求解器所得到的等值线重合度高,说明本文构造的求解器较为可靠。同时两种求解器使用相同的网格,消除了网格差异带来的影响。
|
Fig. 15 Three-dimensional pressure contour and outlet section' s Mach number and pressure contour of rectangular nozzle |
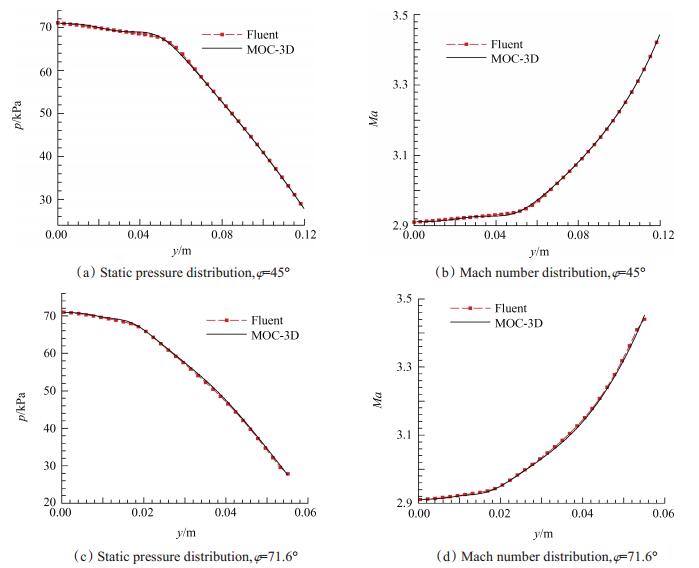
为了获得更加精确地对比,分别在设计流场和数值模拟流场的出口截面提取两条射线上的流动参数,如图 16所示,记该射线与y轴的夹角为φ,两条射线的角度为45°和71.6°。各项流动参数的最大相对误差如表 2所示,其中压力对流场的变化最为敏感,误差最大,但仍在千分之几量级,而马赫数相对误差小至万分之几。
|
Fig. 16 Compare pressure and Mach number along different angles in outlet section |
|
|
Table 2 Max relative error by comparing CFD simulations in outlet section (%) |
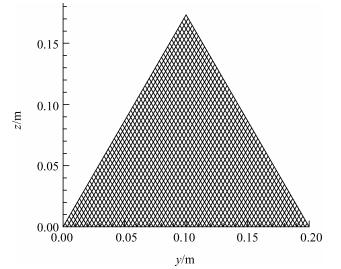
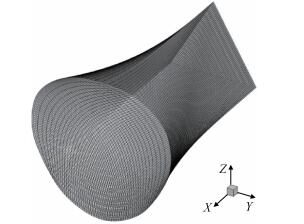
喷管进口为正三角形,边长等于0.2m,如图 17所示,每条边给定61个网格节点,沿x方向空间步进共0.4559m,获得如图 18所示的三维特征网格,网格量约51万。
|
Fig. 17 Mesh of initial-value surface |
|
Fig. 18 Isometric view of the triangular nozzle |
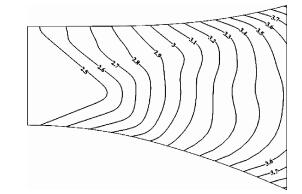
图 19为y=0.1m截面的马赫数等值线,从图中可以看出角区的膨胀较为复杂,马赫线型较为扭曲。但随着膨胀的进行,喷管内部趋于均匀,马赫线型趋于平滑。
|
Fig. 19 Mach number contour in section, y=0.1m |
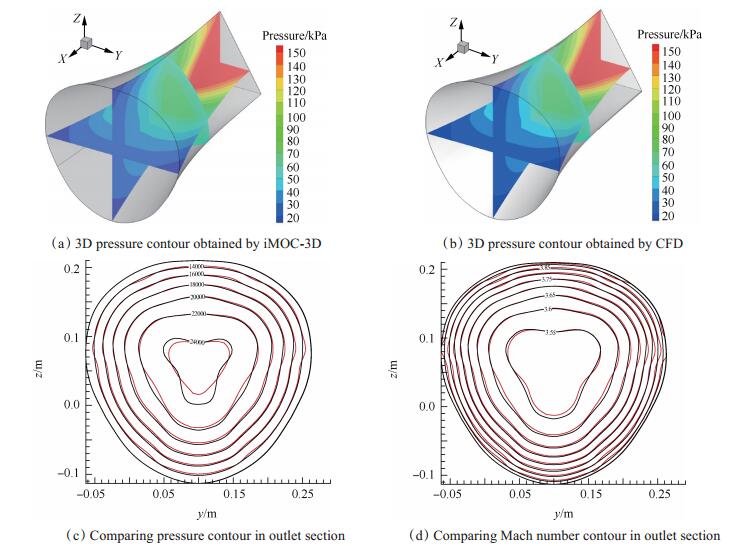
为验证设计方法的可靠性,对获得的三维曲面进行CFD数值模拟,将CFD计算的流场与设计的结果进行对比分析。如图 20(a)~(d)所示,分别为iMOC-3D和CFD计算的三维压力云图以及出口截面的压力等值线、马赫数等值线,其中黑色为iMOC-3D设计流场的等值线,红色为CFD计算得到的等值线。
|
Fig. 20 Three-dimensional pressure contour and outlet section' s Mach number and pressure contour of triangular nozzle |
从上图的对比中可以看出,虽然CFD的计算结果对真实流场具有一定的耗散效应,但两种求解器所得流场基本一致。为了获得更加精确地对比,分别在设计流场和数值模拟流场的出口截面提取了φ=45°以及y=0.1m上的流动参数。如图 21所示,分别对比了沿不同直线的压力、马赫数分布,出口截面各项流动参数的最大相对误差如表 2所示,其中压力相对误差最大,但仍在可接受范围内。

|
Fig. 21 Compare pressure and Mach number along different directions in outlet section |
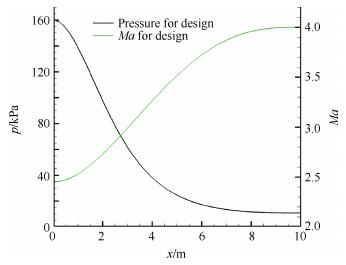
为了进一步探索合理的预设压力分布,本节采用控制壁面马赫数的方式控制壁面压力分布,使得壁面压力过渡更加均匀,不容易出现强压缩波。本节给定如图 22所示的壁面马赫数分布,该分布满足四次多项式,设定壁面进口马赫数为2.45,壁面出口马赫数为4,且初始位置的一阶导数为0,喷管长度为10m,出口位置的一阶导数、二阶导数均为0。通过等熵关系式换算成压力分布,再将其作为求解器的输入项。初始截面仍采用图 8所示的方式划分网格。初始截面为马赫数2.45的平行均匀流,静压、静温、密度等参数保持不变。
|
Fig. 22 Given pressure and Mach number distribution |
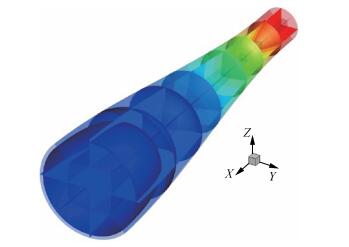
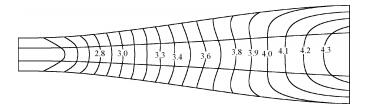
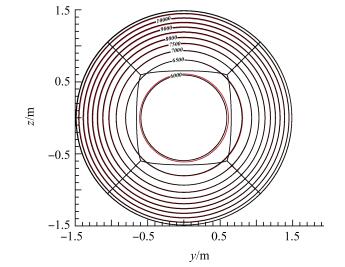
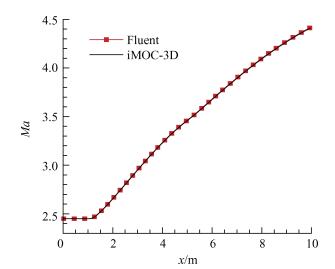
图 23展示了喷管压力等值面的等轴视图;图 24给出了其中一个对称面(Z=0)的马赫数等值线图,可以看出气流在整个喷管内部均匀加速,没有出现强压缩波,具有较高的流场品质。对设计的喷管进行数值模拟,结果如图 25、26所示。图 25对比了出口截面的压力等值线,其中设计流场的等值线为黑色,CFD计算得到的等值线为红色。图 26对比了轴向马赫数分布。
|
Fig. 23 Isometric view of nozzle and 3D pressure distribution |
|
Fig. 24 Mach number contour in section, z=0 |
|
Fig. 25 Comparing pressure contour in outlet section |
|
Fig. 26 Comparing Mach number along central axis |
由图中可以看出,两种不同求解器获得的流场重合度非常高,其中压力和马赫数的最大相对误差为:0.87%,0.12%。流动参数的最大相对误差如表 3所示。说明采用该求解器设计的喷管具有精度较高、壁面参数可控制的优势。
|
|
Table 3 Max relative errors for parameters in outlet section (%) |
综上所述,可得如下结论:
(1)三维超声速压力反问题是非适定的,不具备解的唯一性,本文提出并验证在一定约束条件下,才能确保三维压力反问题解的唯一性。
(2)本文提出的三维超声速压力反问题的双特征线求解技术,可直接根据来流条件和壁面压力分布求解壁面的三维坐标。采用Prandtl-Meyer膨胀波、Busemann进气道的理论解,对该方法进行了精度评估,误差量级均为1×10-4。
(3)采用该方法设计了进口为矩形和三角形的超声速喷管,将设计结果与CFD数值模拟结果进行对比,流场参数的最大误差分别为0.6%,1%,验证了该方法的有效性。
(4)基于该方法及壁面马赫数的构造,设计了均匀膨胀的轴对称喷管,并与CFD结果对比,压力和马赫数的最大相对误差为0.87%,0.12%,验证了该方法对壁面参数的可控性。
| [1] |
Beckel S, Garrett J, Gettinger C. Technologies for Robust and Affordable Scramjet Propulsion[R]. AIAA 2006-7980.
(  0) 0) |
| [2] |
Bulman M, Siebenhaar A. The Rebirth of Round Hypersonic Propulsion[R]. AIAA 2006-5035.
(  0) 0) |
| [3] |
易仕和, 赵玉新, 何霖, 等. 超声速与高超声速喷管设计[M]. 北京: 国防工业出版社, 2013.
(  0) 0) |
| [4] |
Murthy S N B, Thompson H D. Design of Optimized Three-Dimensional Nozzles[J]. Journal of Spacecraft & Rockets, 1966, 3(9): 1384-1393.
(  0) 0) |
| [5] |
Wang X, Damodaran M. Optimal Three-Dimensional Nozzle Shape Design Using CFD and Parallel Simulated Annealing[J]. Journal of Propulsion & Power, 2015, 18(1): 217-221.
(  0) 0) |
| [6] |
Xing X Q, Damodaran M. Design of Three-Dimensional Nozzle Shapes Using NURBS, CFD and Hybrid Optimization Strategies[R]. AIAA 2004-4368.
(  0) 0) |
| [7] |
Moelder S, Szpiro E J. Busemann Inlet for Hypersonic Speeds[J]. Journal of Spacecraft & Rockets, 2015, 3(8): 1303-1304.
(  0) 0) |
| [8] |
Jacobsen L S, Tam C J, Behdadnia R, et al. Starting and Operation of a Streamline-Traced Busemann Inlet at Mach 4[R]. AIAA 2006-4508.
(  0) 0) |
| [9] |
Smart M K. Design of Three-Dimensional Hypersonic Inlets with Rectangular-to-Elliptical Shape Transition[J]. Journal of Propulsion and Power, 1999, 15(3): 408-416. DOI:10.2514/2.5459
(  0) 0) |
| [10] |
Gollan R J, Smart M K. Design of Modular Shape-Transition Inlets for a Conical Hypersonic Vehicle[J]. Journal of Propulsion and Power, 2013, 29(4): 832-838. DOI:10.2514/1.B34672
(  0) 0) |
| [11] |
尤延铖, 梁德旺, 黄国平. 一种新型内乘波进气道初步研究[J]. 推进技术, 2006, 27(3): 252-256. (YOU Yan-cheng, LIANG De-wang, HUANG Guo-ping. Investigation of Internal Waverider-Derived Hypersonic Inlet[J]. Journal of Propulsion Technology, 2006, 27(3): 252-256. DOI:10.3321/j.issn:1001-4055.2006.03.015)
(  0) 0) |
| [12] |
Billig F S, Kothari A P. Streamline Tracing: Technique for Designing Hypersonic Vehicles[J]. Journal of Propulsion and Power, 2000, 16(3): 465-471. DOI:10.2514/2.5591
(  0) 0) |
| [13] |
卢鑫, 岳连捷, 肖雅彬, 等. 超燃冲压发动机尾喷管流线追踪设计[J]. 推进技术, 2011, 32(1). (LU Xin, YUE Lian-jie, XIAO Ya-bin, et al. Design of Scramjet Nozzle Based on Streamline Tracing Technique[J]. Journal of Propulsion Technology, 2011, 32(1).)
(  0) 0) |
| [14] |
Sobieczky H, Dougherty F C, Jones K. Hypersonic Waverider Design from Given Shock Waves[J]. International Hypersonic Waverider Symposium, University of Maryland Collage Park, 1990, 10: 17-19.
(  0) 0) |
| [15] |
Sobieczky H, Zores B, Wang Z, et al. High Speed Flow Design Using Osculating Axisymmetric Flows[J]. Aerospace Science and Technology, 1997, 3: 182-187.
(  0) 0) |
| [16] |
赵博.乘波体飞行器气动外形设计及其数值验证[D].哈尔滨: 哈尔滨工程大学, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10217-1014133727.htm
(  0) 0) |
| [17] |
尤延铖, 梁德旺. 基于内乘波概念的三维变截面高超声速进气道[J]. 中国科学(E辑), 2009(8): 1483-1494. (  0) 0) |
| [18] |
卢鑫, 岳连捷, 肖雅彬, 等.超燃冲压发动机三维变截面尾喷管设计[C].无锡: 第三届高超声速科技学术会议, 2010.
(  0) 0) |
| [19] |
赵玉新.超声速混合层时空结构的实验研究[D].长沙: 国防科技大学, 2008. http://cdmd.cnki.com.cn/Article/CDMD-90002-2008098756.htm
(  0) 0) |
| [20] |
全志斌, 徐惊雷, 莫建伟. 基于控制壁面压力分布的分级单边膨胀喷管设计及试验验证[J]. 推进技术, 2013, 34(3): 307-310. (QUAN Zhi-bin, XU Jing-lei, MO Jian-wei. Design and Experiment Validation of Single Expansion Ramp Nozzle Based on the Control of Wall Pressure Distribution[J]. Journal of Propulsion Technology, 2013, 34(3): 307-310.)
(  0) 0) |
| [21] |
赵玉新, 刘红阳, 赵一龙.三维超声速流动的反问题[C].哈尔滨: 第八届全国高超声速科技学术会议, 2015. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-AGLU201512001102.htm
(  0) 0) |
| [22] |
刘红阳.特征线追踪方法和应用[D].长沙: 国防科技大学, 2015.
(  0) 0) |
| [23] |
李怡庆, 韩伟强, 尤延铖, 等. 压力分布可控的高超声速进气道/前体一体化乘波设计[J]. 航空学报, 2016, 37(9). (  0) 0) |
| [24] |
Cline M C, Hoffman J D. Comparison of Characteristic Schemes for Three-Dimensional, Steady, Isentropic Flow[J]. AIAA Journal, 1972, 10(11): 1452-1458. DOI:10.2514/3.50389
(  0) 0) |
| [25] |
Ransom V H, Hoffman J D, Thompson H D. A Second-Order Numerical Method of Characteristics for Three-Dimensional Supersonic Flow[D]. USA: Purdue University, 1970.
(  0) 0) |
| [26] |
Ransom V H, Hoffman J D, Thompson HD. A Second- Order Bicharacteristics Method for Three-Dimensional, Steady, Supersonic Flow[J]. AIAA Journal, 1972, 10(12): 1573-1581. DOI:10.2514/3.50402
(  0) 0) |
| [27] |
Butler D S. The Numerical Solution of Hyperbolic Systems of Partial Differential Equations in Three Independent Variables[J]. Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Science. The Royal Society, 1960, 255(1281): 232-252. DOI:10.1098/rspa.1960.0065
(  0) 0) |
| [28] |
左克罗MJ, 霍夫曼JD. 气体动力学[M]. 北京: 国防工业出版社, 1984.
(  0) 0) |
| [29] |
童秉纲, 孔祥言, 邓国华. 气体动力学[M]. 北京: 高等教育出版社, 1990.
(  0) 0) |
| [30] |
蓝庆生, 赵玉新, 赵一龙, 等. 三维超声速流动的压力反问题[J]. 空气动力学学报, 2017, 35(3): 429-435. DOI:10.7638/kqdlxxb-2016.0156 (  0) 0) |
 2018, Vol. 39
2018, Vol. 39


