近空间飞行器研究是目前国际竞相争夺空间技术的焦点之一,而近空间高超声速远程机动飞行器的研究又因其重要的战略意义成为近空间飞行器发展的重中之重。吸气式推进系统因为能够提供高的比冲,被认为是在高超声速飞行器领域首选的推进系统[1~3]。大量研究充分证明实现近空间飞行的关键在于推进系统与飞行器机体的匹配设计,其核心则是高超声速飞行器前体与进气道内流通道的设计问题[4~6],即兼顾内、外流性能的飞行器气动布局概念研究,从设计角度考虑,总体对二者的要求存在着差异。
现有的高超声速飞行器多采用前体加常规二维进气道的布局形式(如Hyper-X计划中的X-43、X-51)[7, 8]。由于二维压缩形式构型相对简单,具有较高的工程设计优势,因此,此类方法能够在一定程度上解决前体进气道的设计问题。相对于二维压缩,三维内收缩方式因其高的压缩效率受到国内外众多学者的关注[9~13]。高超声速三维内收缩进气道是一种区别于典型高超声速进气道(轴对称进气道、二元进气道、侧压进气道)的进气道形式。与常规二维压缩相比,美国空军实验室研制的一种三维Jaw进气道获得了24.87%推力增益[9, 10];美国与澳大利亚联合试射了马赫数10的HYCAUSE飞行器验证了内收缩式进气道的工作特性[11];此外,洛克希德马丁公司为美国下一代高超声速飞行器FALCON采用的方案也为三维向内收缩的方式[12]。可以看出,高超声速进气道的压缩形式向三维内收缩转变将成为可能。因此前体三维内转进气道的匹配设计已成为高超声速气动设计领域亟需解决的关键问题之一。
然而,三维内转进气道通常具有极其复杂的压缩型面,该三维特征为前体与进气道的设计引入了困难。在国际上,Kothari等[14]提出直接将进气道作为飞行器前体,该方法将前体与三维进气道完全融合。虽然一定程度上解决了前体与三维内转进气道的匹配问题,但由于全场采用内收缩流场设计,该飞行器方案的升阻特性将受到严重影响。Smart基于REST进气道,提出了将REST进气道[15]多模块并列安装在类似X43C的二维飞行器前体的下表面上[16],这一做法仅从几何上将三维内转进气道匹配于二维前体,从设计角度来看并不存在本质创新。在国内,李璞等对一种带前体的高超声速矩形转圆形进气道进行了试验研究[17],该试验物理模型采用等面积逐渐过渡的形式将具有二维前体的矩形进气道进口过渡为圆形出口,研究结果表明,由于该方案在前体部分采用纯二维平面压缩,横向溢流较为明显,必须对前体外形进行优化设计以提高性能。向先宏等[18]基于类咽式进气道实现了该类进气道与楔导乘波前体的匹配设计,为前体与三维内收缩进气道的匹配提供了设计思路。
因为乘波前体与三维内收缩进气道截然不同的压缩形式,前体激波与进气道三维内锥激波将产生严重的相互干扰,所以前体与进气道的设计绝非仅仅将两个部件分别设计再进行折衷叠加,而应该是最大程度的兼顾两部分的优点,并减弱两部分之间的相互影响。两部分之间的相互干扰很大程度上是由于激波曲面之间相互不兼容而引起的,即乘波体所具有的外压缩激波与三维内转进气道所需的内压缩激波之间存在的相互干扰问题。为解决以上问题,本文从激波匹配设计的角度出发,以传统的三维内转进气道设计方法为基础,设计乘波前体。
2 气动融合设计 2.1 设计思路本节从激波气动匹配的角度出发,预实现一种乘波前体与三维内转进气道的气动融合设计。该设计方法将在流场上游产生二维入射斜激波,随着流场向下游发展,下游流场将产生适合于三维内转进气道的三维内收缩流动,从而实现二维乘波流动向三维内收缩流动的转变。
乘波前体三维内转进气道具有两级入射激波,包括前体二维入射激波与三维内转进气道入射内锥激波。因此,欲实现以三维内转进气道为基础匹配设计乘波前体,需要在设计之初构造如图 1所示的双波入射三维内转进气道。该进气道运用流线追踪法在指定双波入射基本流场中按内乘波理论生成,具有前缘入射内锥激波(Initial conical shock)与第二道入射内锥激波(Second conical shock)的两级压缩。值得注意的是,两道入射内锥激波并未汇聚于进气道唇口处。在设计过程中保留第二道入射内锥激波不变,仅将前缘入射三维内锥激波向乘波前体二维入射激波转化,得到所需的流场结构。

|
图 1 Inward turning inlet with double conical shock |
为进一步说明设计思路,本文提取了对称面上流动特征进行分析。流场结构如图 2所示。图 2中压缩型面具有两级压缩角(δ1,δ2),在轴对称回转流场中,有意设计两道入射内锥激波位置,使它们不汇聚于对称轴。当AB段回转母线由三维内收缩流动变换为二维平面压缩时,产生的二维平面激波(Initial 2D shock)恰好与第二道内锥激波汇聚在中心处。如此一来,当前体AB段的流动特征由轴对称内收缩转变为二维平面压缩后,在对称面上能够获得封口的二维平面入射激波和三维内锥激波。因此,设计的要点是初始转折角δ1的选取。在全三维内收缩情况下,转折角δ1将产生图 2中红色实线所示的初始三维内锥激波,而在二维情况下转折角δ1能够产生图 2中红色虚线所示的二维入射激波。

|
Fig. 2 Schematic of the flow field (Symmetry-plane) |
图 3为双波入射基本流场,如图所示,该流场具有两道气流转折角,初始转折角δ1为8°,第二道转折角δ2为10°。流场中存在前缘入射内锥激波与第二道内锥激波(图 3中红色虚线),两波不相交。而根据斜激波关系式,可以预测出图 3中虚拟乘波前体二维入射激波(黄色虚线),虚拟二维平面激波与第二道内锥激波(红色虚线)恰好汇聚于回转中心轴线。此外,需要说明的是,第二道转折角的选取将决定第二道内锥激波的强度,当转折角较小时,内锥激波将弱化为内锥压缩波,但该现象并不影响本文所研究的设计思路的实现。

|
图 3 Inviscid pressure ratio of the basic flow field |
乘波前体三维内转进气道设计的难点是乘波前体与三维内转进气道压缩方式的不同。在横截面图上,传统三维内转进气道的流动特征如图 4右半幅所示,流场表现为全三维向内压缩。入射激波为三维内锥激波面。该激波在横截面内具有圆弧向内收缩的趋势,如图 4中的Initial conical shock和Second conical shock所示。而对于采用二维乘波压缩方式的飞行器前体,初始入射激波为二维斜激波面。该激波在横截面内表现为平面向下压缩的方式,如图 4左半幅中Initial 2D shock所示。因此,设计关键在于构造兼顾上游二维乘波压缩与下游三维向内压缩的流场结构,具体如图 4中左半幅所示,图中乘波前体具有典型的二维平面压缩,发展至下游进气道部分则由二维平面压缩转变为三维向内压缩。

|
Fig. 4 Schematic of the flow field (Cross-section) |
乘波前体三维内转进气道的气动融合设计,必须结合三维内转进气道的流场特征。图 4右半幅中以进气道前缘捕获形状(3D capture shape)在流场中进行流线追踪,能够得到进气道喉道出口形状。分析图 4右半幅可以发现,三维内转进气道的捕获形状被由内收缩基本流场圆心点O向外生成的射线OD分为激波生成段与激波接收段两部分。由激波生成段(点A)生成的内锥激波将汇聚于激波接收段(点C)。该特征为匹配设计提供了思路。若根据二维斜激波理论,以激波接收段为起始,匹配求解二维斜激波面进而获得乘波前体所需的压缩型面,就可以将图 4中右半幅所示流场结构转化为左半幅中的二维加三维流场结构。
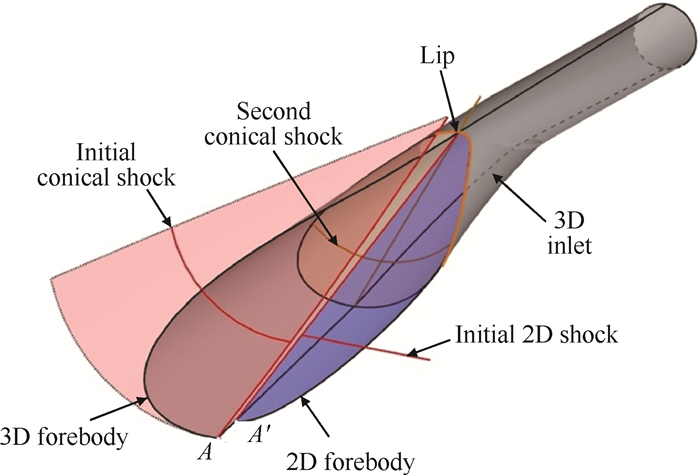
结合匹配设计的流向流场结构与横向流场结构能够得到乘波前体三维内转进气道三维流场结构,如图 5所示。图中左半幅表示双波入射三维内转进气道,右半幅表示乘波前体三维内转进气道。从图中可以明显看出两方案在流场结构上的不同,对于双波三维内转进气道,入射激波为两道内锥激波。而乘波前体三维内转进气道则将前缘入射内锥激波(图 5中红色激波面)转化为二维入射激波(图 5中蓝色激波面),且该激波将与第二道内锥激波同时汇聚于三维内转进气道激波接收段。
|
Fig. 5 Schematic of the flow field (Three-dimensional) |
图 6为采用上述设计方法得到的乘波前体三维内转进气道。设计来流马赫数Main=6.0,总收缩比CR=5.5。

|
Fig. 6 Orthographic views of inward turning inlet with waverider forebody |
本文针对图 6所示乘波前体三维内转进气道采用商业计算软件Fluent在设计与非设计状态下分别进行了全粘性的N-S方程数值求解,图 6中所示模型总长度为3000mm,来流条件如表 1所示。无粘通量采用2阶Upwind的Roe-FDS格式,粘性通量采用中心差分格式进行离散,湍流模型采用k-w SST两方程模型。考虑到气体的高温效应,计算中采用考虑变比热的热完全气体模型。分子粘性系数采用Sutherland公式计算。当各残差指标下降至少3个数量级,且出口流量守恒时,可判定计算收敛。
|
|
Table 1 Parameters used for numerical simulation |
为了检验所采用计算方法的可靠性,本文采用文献[19]中的GK01模型进行数值模拟,用以验证本文模拟方法的正确性。GK01模型尺寸参数如图 7所示,为二维混压进气道,外压缩段采用两级压缩,唇口平直。设计飞行马赫数为Ma=7.0,喉道位置采用等熵膨胀过渡。

|
Fig. 7 Model of GK01 (mm) |
|
|
表 2 Test parameters of GK01 |
根据文献[20]研究可知,图 7中的GK01进气道模型宽度为100mm,且存在侧壁,因模型对称,仅取模型的一半进行网格划分,其结构网格与计算域分布如图 8所示,其中蓝色区域为进气道侧壁。绿色区域为进气道压缩面。

|
Fig. 8 3D Mesh of GK01 |
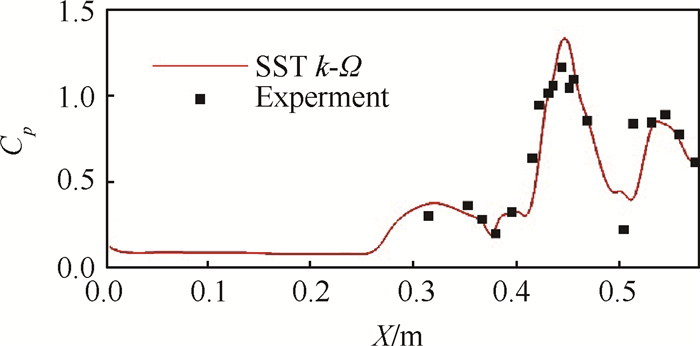
对图 8中的网格进行数值模拟,并提取计算结果中GK01模型对称面下壁面沿程静压分布与试验数据进行对比。结果如图 9所示,可以看出,本文计算得到的壁面沿程静压分布与试验数据吻合良好。这表明本文使用的数值模拟方法是可行的。
|
Fig. 9 Static pressure along the wall |
图 10为计算采用的结构化网格,考虑到对称性,仅取对称面一侧划分网格。计算域细分为20块,其中进气道进口外侧布置一块网格,用于计算可能产生的溢流。为验证计算网格的无关性,本文分别对总单元数为150万,300万和500万的网格进行数值模拟,并提取前体进气道对称面上表面马赫数分布如图 11所示,图中三个数量不同的网格之间存在差异较小,因此本文选取总单元数300万的网格进行后续的数值模拟研究。近壁面进行了等比加密处理,近壁最小网格高度0.01mm,y+ < 10。此外,由于进气道三维造型的复杂性,最后对生成的网格进行了全局正交性优化。对壁面取绝热无滑移、固体边界条件,进出口分别采用压力远场和压力出口边界条件,XZ切面给定对称面边界条件,计算过程中为方便流场收敛采用来流参数对流场进行初始化。

|
Fig. 10 Mesh for the inward turning inlet with waverider forebody |

|
Fig. 11 Comparison of mach number distribution at different grid scales employed in the ramp of hypersonic inlet |
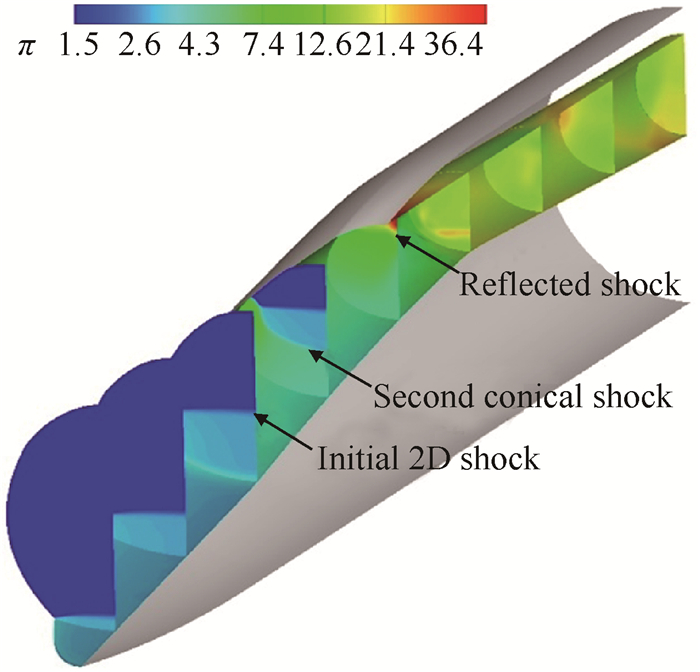
为说明乘波前体三维内转进气道具有的波系结构,本文从计算结果中提取了压力梯度的数据,如图 12所示,图中给出了壁面的压力分布用以显示三维激波结构的背景压力,并给出了三维激波结构的压比分布图。可以看出,高超声速来流首先在前体前缘产生了深蓝色(压升较低)的封口入射二维斜激波(Initial 2D shock),随着气流向下游发展,在三维内转进气道前缘处产生了浅蓝色(压升较高)的三维内锥激波(Second conical shock),两激波共同作用将进气道进口封闭并于唇口附近相汇聚开始发生反射。三维反射激波(Reflected shock)交进气道于下壁面肩部附近,并再次反射,最终形成如图 12所示的三维激波结构。

|
Fig. 12 Static pressure iso-surfaces of the forebody/inlet |
乘波前体三维内转进气道两道入射激波在对称面处较好地还原了设计的流场结构。然而沿周向发展,乘波前体二维入射激波未能完全汇聚于三维内转进气道激波接收段,因此在唇口边缘处出现了一定的激波干扰现象,但根据下文对出口特性的分析可以发现,该现象对进气道的总体性能并未产生影响。
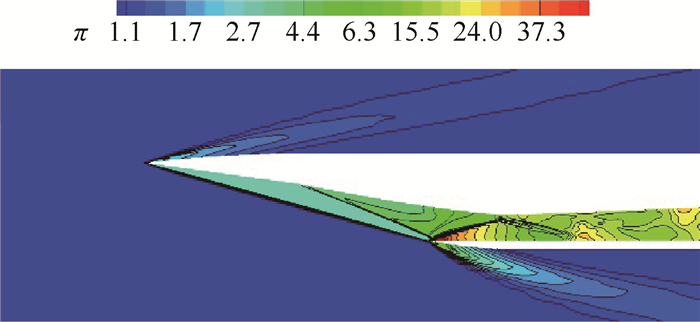
图 13为计算获得的乘波前体三维内转进气道在设计状态下的沿程各截面压比分布等值图。可以看出,前体前缘产生的入射激波(Initial 2D shock)保持了二维激波的平面压缩特性,但因为本文提出的设计方法在前体段并未严格遵守楔导乘波理论,故在前体边缘处激波出现了一定的衰减,导致前体入射激波与前体压缩型面在边缘处存在微小的“缝隙”,小部分流量将会从其间泄露,产生溢流。但该“缝隙”仅占整个进口面积的很小一部分,对流量损失影响较小。气流进入三维内转进气道部分后,在进气道前缘产生了第二道入射激波(Second conical shock),该入射激波具有典型的三维内收缩激波的特征,表现为逐渐向中心汇聚,并交于唇口附近。
|
Fig. 13 Static pressure contours of the forebody/inlet (α=0°) |
图 14为设计状态下的对称面压比分布等值图。通过流场的压比分布能够发现,在乘波前体段具有典型的二维压缩特征,而在三维内转进气道部分则表现为典型的三维内收缩的流动特征。对于二维压缩,高超声速来流经过初始斜激波压缩后将不再产生压力上升,表现为波后压力趋于一致。而三维向内压缩,经过初始入射内锥激波的压缩后在流场的发展过程中还将产生额外的等熵压缩。因此,观察图 14的压比分布可以发现,在乘波前体入射斜激波与三维内转进气道入射内锥激波之间不存在等熵压升,而气流经过进气道入射内锥激波后,受到等熵作用波后仍然存在压力升高的特性。通过对称面流场的压比分布能够证实,本文所研究的匹配设计方法能够构造出上游二维流动加下游三维内收缩流动的流场结构。
|
Fig. 14 Static pressure contours in the symmetry plane (α=0°) |
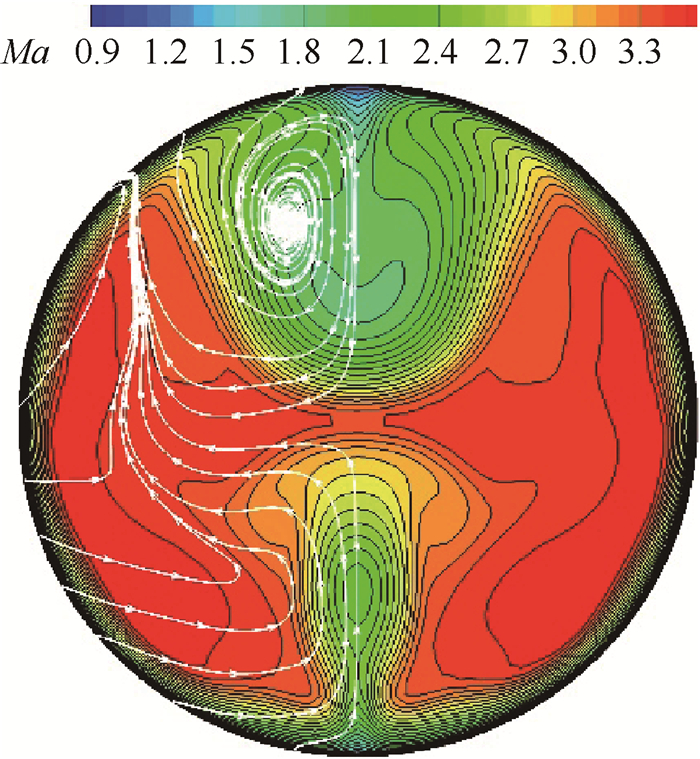
图 15为进气道出口马赫数分布图,从图中可以看出高速高能气流主要分布在两侧,在压缩面(对称面上部)与唇罩(对称面下部)一侧形成两个低能涡流区。且通过隔离段出口马赫数等值分布图可以发现,在压缩面一侧产生了较大的涡流区域。该区域主要由唇罩反射激波压缩气流在唇罩侧产生初始涡流区,随着气流向下游发展,该涡流区受唇罩激波波后高压区的压缩产生上洗趋势,导致在隔离段流动中低能气流不断由两侧向压缩面一侧汇聚,最终在隔离段出口处形成了较大的涡流区域,导致出口总压恢复图谱中在压缩面一侧气流品质较差。
|
Fig. 15 Mach number contours in the exit section |
在设计状态与非设计状态下对乘波前体三维内转进气道进行了全粘性数值模拟,计算结果如表 4所示。从表中可以看出,根据上文所述设计方法已经最大程度抑制波后溢流,因此,进气道在设计条件下(Main=6.0)流量捕获系数能够达到0.96,在非设计点(Main=4.0)仍能保持约0.71的流量捕获能力。出口平均性能同样显示,流场内三道强激波的作用并未产生额外的气流损失,其设计点出口总压恢复系数仍能保持在0.53左右。总体而言,乘波前体三维内转进气道的流量捕获系数及总压恢复系数在零攻角状态下均能够保持在较高水平。
|
|
Table 4 Performance of the inlet outflow (α=0°) |
此类前体进气道由于前体的存在,在长度上相对于传统的三维内转进气道有一定的增加,这将导致进入进气道内压缩段的边界层低能流区域的增大,从而影响进气道的自起动性能。在实际应用中,若要求较低的自起动马赫数,将不可避免地引入抽吸泄流等流动控制技术。
3.4 攻角状态流场结构分析除了设计状态工作特性,攻角条件下的性能在一定程度上决定着推进系统的可工作范围。图 16为6°攻角情况下乘波前体三维内转进气道对称面压比分布等值图。可以看出,在相同的来流条件下,随着攻角的增大,经过乘波前体二维斜激波面压缩后压升有所提高。根据图谱颜色的深浅可以发现,进气道内部的压缩程度也得到了增强。图 16中随着攻角的增大在进气道唇口将出现激波干扰的现象。从对称面流场可以发现,乘波前体前缘产生的入射激波不再与三维内转进气道产生的三维内锥激波汇聚于唇口点,而是入射至内锥激波中部,该现象主要是由攻角作用与激波的三维效应引起。

|
Fig. 16 Static pressure contours in the symmetry plane (α=6°) |
对比图 17,前体进气道6°攻角时的流场切面图与图 13设计状态下流场的切面图可以发现,引入攻角之后乘波前体前缘产生的二维激波角度有所减小,而进气道产生的三维激波仍然具有向唇口汇聚的趋势,且因为前体二维激波的影响减弱,向中心汇聚的趋势更加明显,如图 17中红圈内流场所示。横侧向激波逐渐向对称面汇聚,最终表现为唇口附近激波偏离压缩面的程度增大,故出现了图 16中唇口附近的波系结构。

|
Fig. 17 Static pressure contours of the forebody/inlet (α=6°) |
在攻角状态下对乘波前体三维内转进气道进行了全粘性数值模拟,计算结果如表 5所示。在3°攻角时,对称面内的波系结构相较0°攻角时虽然未发生显著改变,但是波强有所增加,因此在出口处的压比上升,马赫数下降。且随着攻角的继续加大,上述流场变化得到进一步增强,波系结构也将相应出现变化。6°攻角时的出口压比29.69相较0°攻角时的出口压比17.22增长了约72%,而出口马赫数也从0°时的3.09降为2.58。进气道流量捕获系数不断上升,当攻角为6°时能够捕获设计来流流量的123%。结合前文分析,本文认为,尽管本文所研究乘波前体三维内转进气道完全按照设计状态参数和要求进行设计,但在非设计状态下,进气道内部的流场大都还遵循其设计状态下的流动特征,总体性能上都具有不俗的表现。
|
|
Table 5 Performance of the inlet outflow (α≥0°) |
采用典型的前体二维混压式进气道与本文所研究设计方法进行对比,两类方案在设计时遵循捕获面积,设计飞行高度,飞行马赫数相同且同时保证两方案设计点隔离段出口马赫数大致相同,在Ma=3.0~3.1。以上约束基本确定了进气道捕获流量、设计点以及压缩量等设计条件,以此提高两方案的可比性。
根据以上设计条件设计了前体二维混压进气道模型如图 18所示,该模型具有包括前体在内的四道入射斜激波,采用斜激波最优设计理论生成压缩型面。此外,为减小二维进气道的横向溢流损失以更加准确的比较两方案,在第二压缩面起始处添加侧板,如图 18(Side wall)所示。添加侧板后,进气道性能将明显优于常规方案。
图 19(a),(b)为两方案对称面流场马赫数分布图,两方案在前体前缘处产生一道入射斜激波。对于内转进气道方案,在入射斜激波之后跟随一道三维内锥激波,波后成等熵压升趋势,而前体二维混压进气道方案入射斜激波后为三道入射斜激波。两方案波系均能于唇口处汇聚并实现反射,减弱了设计状态下的唇罩溢流。然而根据表 3计算结果对比可知,虽然通过优化波系结构两方案均能实现唇罩无溢流,但前体二维混压进气道由于未按照乘波理论设计,相对于乘波前体三维内转进气道仍然存在一定量的横向溢流损失。这点将在后续的性能对比中进一步分析。
|
|
Table 3 Comparison of invisicid and viscous performance of the inlet outflow |
由表 6可知,设计状态与非设计状态下,乘波前体三维内转进气道与前体二维混压进气道的总体性能参数尤其是流量系数存在较大差异。因为两方案在设计之初遵循了相同的设计条件,所以在设计状态下(Ma=6.0)隔离段出口马赫数相差较小,但前体二维混压进气道由于前体横向溢流的影响流量系数相对乘波前体三维内转进气道降低了约4.1%。
|
|
Table 6 Performance comparisons of two inlets with forebody under different incoming Mach numbers |

|
Fig. 18 Model of two dimensional inlet with forebody |
在非设计状态下,因入射激波偏离唇口,进气道产生唇罩溢流,两类前体进气道流量系数均有下降,且由于二维进气道相对于三维内转进气道将存在更大的溢流窗,所以在Ma=5.0时前体二维混压进气道较乘波前体三维内转进气道流量降低了11.7%,远高于设计状态时的流量差。该趋势在Ma=4.0时表现得更为明显。可以说,在设计状态下能够设计出气动性能相似的前体进气道方案,但乘波前体三维内转进气道能够更好地兼顾非设计状态下的气动性能。

|
Fig. 19 Mach number contours in the symmetry plane |
本文发展了一种具有乘波压缩特征的前体三维内转进气道匹配设计方法。基于该方法设计出了一种乘波前体三维内转进气道,对其设计点与非设计点进行全三维数值模拟,并与典型前体二维混压进气道进行对比研究,得出以下结论:
(1)因二维平面压缩与三维向内压缩截然不同的压缩形式,首先应设计具有全三维内收缩特征的双波入射基本流场,进而根据三维流动与二维流动之间的相互关系,按照斜激波理论,将三维内收缩流动向二维加三维压缩形式转化,用以完成前体进气道匹配设计。
(2)乘波前体三维内转进气道的数值模拟结果显示,在设计状态(Main=6.0)进气道流量捕获系数能够达到0.96,且具有0.53的总压恢复系数;在非设计状态(Main=4.0)进气道流量捕获系数仍能保持在0.71,总压恢复系数为0.70,从而保证了进气道的高性能要求。
(3)与典型的前体二维混压进气道进行对比研究,乘波前体三维内转进气道方案总体性能提升明显,尤其是进气道流量捕获系数在设计状态下较二维方案上升了4.1%,且该趋势在非设计点表现更为明显。
| [1] |
Kuranov A, Korabelnikov A. Atmospheric Cruise Flight Challenges for Hypersonic Vehicles under the Ajax Concept[J]. Journal of Propulsion and Power, 2012, 24(6): 1229-1247.
(  0) 0) |
| [2] |
尤延铖, 梁德旺, 郭荣伟, 等. 高超声速三维内收缩式进气道/乘波前体一体化设计研究评述[J]. 力学进展, 2009, 39(5): 513-525. DOI:10.3321/j.issn:1000-0992.2009.05.001 (  0) 0) |
| [3] |
Nonweiler T R F. Aerodynamic Problems of Manned Space Vehicle[J]. Journal of the Royal Aeronautical Society, 1959, 63: 34-40.
(  0) 0) |
| [4] |
Francois F, Laurent S. The French LEA Flight Test Program-Status in 2008[R]. AIAA 2008-2541.
(  0) 0) |
| [5] |
Lewis M. A Hypersonic Propulsion Airframe Integration Overview[R]. AIAA 2003-4405.
(  0) 0) |
| [6] |
贺旭照, 周正, 倪鸿礼. 密切内锥乘波前体进气道一体化设计和性能分析[J]. 推进技术, 2012, 33(4): 510-515. (HE Xu-zhao, ZHOU Zheng, NI Hong-li. Integrated Design Methods and Performance Analyses of Osculating Inward Turning Cone Waverider Forebody Inlet(OICWI)[J]. Journal of Propulsion Technology, 2012, 33(4): 510-515.)
(  0) 0) |
| [7] |
Mcclinton C. X-43 - Scramjet Power Breaks the Hypersonic Barrier: Dryden Lectureship in Research for 2006[R]. AIAA 2006-1.
(  0) 0) |
| [8] |
Hank J, Murphy J, Mutzman R. The X-51A Scramjet Engine Flight Demonstration Program[R]. AIAA 2008-2540.
(  0) 0) |
| [9] |
Malo-Molina F J, Gaitonde D V, Ebrahimi H B, et al. Three-Dimensional Analysis of a Supersonic Combustor Coupled to Innovative Inward-Turning Inlets[J]. AIAA Journal, 2010, 48(3): 572-582. DOI:10.2514/1.43646
(  0) 0) |
| [10] |
Malo-Molina F, Gaitonde D, Ebrahimi H. Numerical Investigation of a 3-D Chemically Reacting Scramjet Engine at High Altitudes Using JP8-Air Mixtures[R]. AIAA 2005-1435.
(  0) 0) |
| [11] |
Walker S, Rodgers F. Falcon Hypersonic Technology Overview[R]. AIAA 2005-3253.
(  0) 0) |
| [12] |
Walker S, Sherk J, Shell D, et al. The DARPA/AF Falcon Program: The Hypersonic Technology Vehicle #2 (HTV-2) Flight Demonstration Phase[R]. AIAA 2008-2539.
(  0) 0) |
| [13] |
尤延铖, 梁德旺, 黄国平. 一种新型内乘波式进气道初步研究[J]. 推进技术, 2006, 27(3): 252-256. (YOU Yan-cheng, LIANG De-wang, HUANG Guo-ping. Investigation of Internal Waverider-Derived Hypersonic Inlet[J]. Journal of Propulsion Technology, 2006, 27(3): 252-256. DOI:10.3321/j.issn:1001-4055.2006.03.015)
(  0) 0) |
| [14] |
Kothari A P. Designs of and Methodology for Inward or Outward, and Partially Inward or Outward Turning Flow Hypersonic Air-Breathing and Rocket-Based-Combined-Cycle Vehicles[P]. US 6164596A, 2000-12-26.
(  0) 0) |
| [15] |
Smart M K. Design of Three-Dimensional Hypersonic Inlets with Rectangular-to-Elliptical Shape Transition[J]. Journal of Propulsion and Power, 1999, 15(3): 408-416. DOI:10.2514/2.5459
(  0) 0) |
| [16] |
Trexler C A, Smart M K. X-43C Inlet Development and Testing[R]. USA: JANNAF Meeting, 2003.
(  0) 0) |
| [17] |
李璞, 郭荣伟. 一种带前体的高超声速矩转圆形进气道研究[J]. 航空学报, 2009, 30(4): 625-629. DOI:10.3321/j.issn:1000-6893.2009.04.008 (  0) 0) |
| [18] |
向先宏, 王成鹏, 程克明. 基于类咽式进气道的高超声速飞行器一体化设计[J]. 宇航学报, 2012, 33(1): 19-26. DOI:10.3873/j.issn.1000-1328.2012.01.003 (  0) 0) |
| [19] |
H berle J, Gülhan A. Investigation of Two-Dimensional Scramjet Inlet Flowfield at Mach 7[J]. Journal of Propulsion and Power, 2008, 6.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


