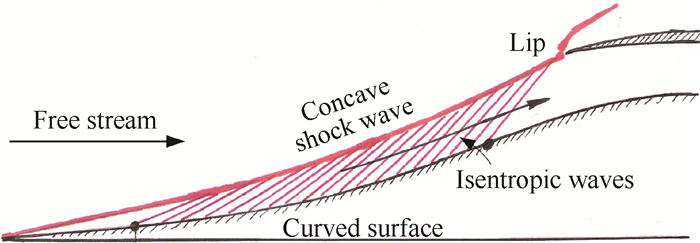
高超进气道就是压缩高超来流、减速增压到适合发动机工作的气流通道。在严酷的高温、高压气动载荷和空间与结构质量的限制下,设计宗旨应该是希望所有参与气流压缩的表面积尽量小,或者是所有接触气流的表面都参与对高速气流的压缩,即每一寸压缩面都对气流压缩作贡献。那什么样的压缩面才可能有这样的功效?答案就是:“曲面压缩”。图 1就是曲面压缩概念的示意图。
|
Fig. 1 Schematic diagram of curved surface compression system |
曲面压缩面通常由一小段前缘斜楔和随后特殊设计的内凹弯曲压缩面组成。前缘斜激波后的超声气流在曲面压缩面上按预定的规律继续压缩,产生一系列等熵压缩波并分别与前缘激波相互作用,迫使前缘激波逐渐增强并向外侧弯曲,弯曲激波及其后的等熵波共同完成对高速气流的压缩,真正实现了与气流接触的整个表面都参与了对气流的压缩,即每一寸压缩面都发挥了对气流压缩的功效。一般情况下曲面压缩大都伴随着弯曲激波,常规的等熵压缩实际上是曲面压缩的特例。
随着高超声速技术特别是超燃冲压发动机技术的快速发展,高超声速进气道设计也面临着一系列挑战性问题,例如进气道与燃烧室的一体化设计、进气道与飞行器前体的一体化设计、进气道巡航状态性能与宽范围工作性能的矛盾、流道附面层分离和流态的控制、压缩面的减阻等问题[1~3]。
曲面压缩概念的提出为解决这些问题提供了新的途径。研究表明,曲面压缩进气道在降低总压损失、缩短长度、避免附面层分离、改善非设计点性能等方面均存在优势,因此逐渐受到人们关注,对这种流场的设计方法、性能与应用已进行了多方面的探索和详细的研究,并取得了丰硕的成果[4]。
需要指出的是,超声进气道曲面压缩的概念最初只是希望在高超风洞上,尽可能缩短进气道压缩面长度,提供尽可能大尺寸的高性能高超进气道模型气动设计。在穷尽所有可能的构思后,忽然顿悟若将二维平面斜楔压缩面由平面变为凹曲面,用无限多级斜楔代替有限级数的斜楔压缩,让等熵压缩波依次交汇并迫使激波弯曲,这样不仅缩短了压缩面长度,在局促的空间限制下,模型可以做到较大,而且引入了部分的等熵压缩替代纯激波压缩,尽管激波损失有所增加,但总压损失基本相当,且总体气动性能另有优势。这一发现当时真有“柳暗花明又一村”之感。经过近20年十余名博士、硕士的不懈研究,发现这种压缩方式很有特色,至今已发展了高超压缩面多种正向设计和逆流向反向设计的设计方法,值得深入研究和继续开发。
本文对目前曲面压缩相关的研究进行了回顾和展望,包括几种新概念的设计方法和取得的成果,为其进一步发展和工程应用提供借鉴。
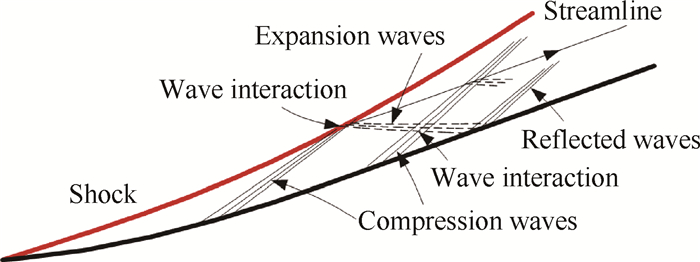
2 曲面压缩的流场特征常规的斜激波压缩、等熵压缩壁面发出的特征线均为直线,通过斜激波关系、Prandtl-Meyer方程容易对流场进行计算和分析。而曲面压缩流场较为复杂,见图 2,其中不仅包含前缘激波和等熵压缩波,两者相互作用还会形成反射波系、滑流间断,反射波系和滑流间断又将继续与下游的压缩波产生相互作用,进而影响壁面附近流动,因此压缩面发出的左行特征线不再是直线。文献[5]通过对波系相互作用的分析提出了曲面压缩流场细节及特征参数的近似计算方法。文献[6~8]研究了弯曲激波附近参数与激波曲率之间的关系。
|
Fig. 2 Schematic diagram of waves in curved surface compression flow field |
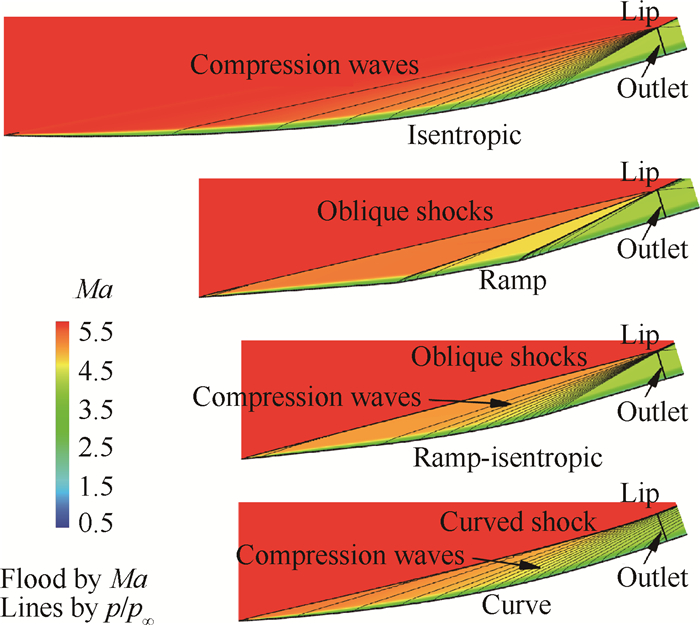
图 3给出了相同捕获高度、相同压比下,一种典型的二元曲面压缩流场与传统等熵压缩、等激波强度三级斜楔压缩、斜楔-等熵压缩流场共四种压缩波系构成的对比。图中下标∞表示来流参数。
|
Fig. 3 Mach number and pressure contour of four types of compression flow field |
从图 3可见曲面压缩达到指定压比所需的长度明显短于等熵压缩和斜楔压缩。流场计算结果表明,与三种常规的压缩相比,曲面压缩流场出口附面层厚度、形状因子也更低,而且在来流马赫数降低时其流量捕获变化更小[9]。
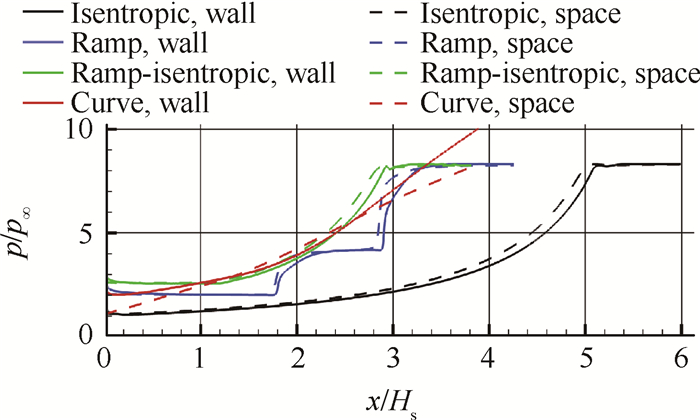
图 4为上述四种压缩流场壁面及空间压力变化曲线,其中x对应的空间压力分布为壁面该点与唇口位置连线上气流压力的流量加权平均值,Hs为捕获高度,可见实现同样的压升,纯等熵压缩的压缩面长度最长,压缩过程初始阶段压升缓慢,而后压升逐渐加快,即压力梯度沿程增加;斜楔+等熵压缩的方式可以缩短压缩面长度,但压力梯度的规律基本相同;等强度三级斜楔压缩完全靠三道斜激波压缩,斜激波后的楔面基本上不参与对气流的压缩;图中给出的某种曲面压缩,它的压升规律较为平缓,避免了压缩面末端压力陡升的现象,它的空间压升曲线非常接近等压力梯度规律,而且压缩面长度也与三楔压缩相当。
|
Fig. 4 Pressure distribution on the wall and in the space of four types of compression |
曲面压缩中激波压缩和等熵压缩的比例是完全可控的,这是曲面压缩的一大优势。研究表明,曲面压缩能更为灵活地配置压缩过程的参数变化,有更多设计参数可以根据不同的具体需要加以调整和控制,实现最佳的波系配置。
一般的曲面压缩包含下列三要素:(1)曲面压缩面;(2)弯曲激波;(3)曲面压缩面与弯曲激波间的压缩流场。
其中曲面压缩面是这种压缩方式的核心,现已创造并发展了多种设计方法。下文将简要总结-评述-展望这一超声/高超曲面压缩的主要设计方法及其主要特征,包括曲面压缩的正向设计和逆流向的反设计以及给定压缩面气动参数分布规律的反设计等。
3 正向设计方法根据流场波系分析可知,壁面曲率略大于等熵压缩型面使压缩波逐渐与前缘激波相交即可形成弯曲激波,因此一个最直接、最简单的方法就是沿流向适当“压迫”经典的等熵压缩型面,让等熵压缩波逐次相交就能够形成具有弯曲激波的曲面压缩流场。
2012年法国图尔18届AIAA高超会议上,在与加拿大Sannu Molder教授的个人交流中,他也提出了这种“压迫”等熵流场的概念,并给出了具体的数学公式,即将等熵压缩面的x坐标乘以一个给定的收缩系数,例如取收缩系数为0.8,那新设计的压缩面流向坐标就是
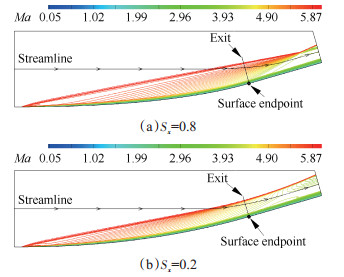
|
Fig. 5 Curve surface compression flow field with different scale factor Sx |
如果取缩放因子Sx为某种函数表达式来代替常数,例如令
此外,居燕[11]系统地研究了二次函数形式的弯曲压缩型面,潘瑾[12]研究了指定压缩角变化规律的压缩型面,给出了前缘压缩角、型面曲率等设计参数对激波形状、压缩性能的影响规律。
总体来看,正向设计方法容易实现,但由于设计参数往往没有明确的物理意义,并且与性能参数之间关联比较复杂,不利于达到所需的性能要求。这种曲面压缩面的设计方法基本上属于几何设计而非气动设计。而通过对流场气动参数的需求直接进行反设计是更科学合理的途径,对此方法已取得许多研究成果。
4 由出口参数反设计压缩通道直接根据下游参数分布的需求设计流道能够避免设计过程的迭代,对进气道设计有重要意义。
方兴军[13]以二维有旋特征线理论作为设计工具,分析了逆流向推进计算的理论依据和实现条件,提出了给定出口速度分布反设计超声速流道的方法,其中包括根据出口参数确定弯曲激波形状、根据弯曲激波反设计压缩型面、沿特征线从下游向上游反设计、前后流场的装配等过程(参见图 6)。数值计算和风洞试验表明了该方法的正确性[14]。韩伟强等[15]进一步提出了不需上游参数仅通过出口参数逆向设计流道的方法。此外,文献[16]详细分析了弯曲激波形状对流场性能的影响规律。
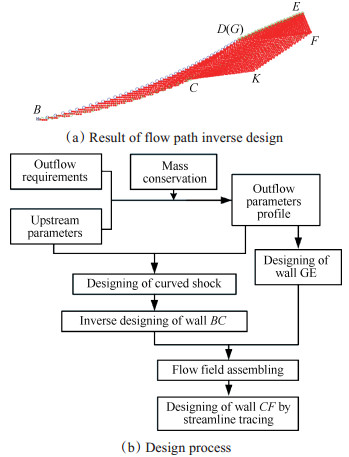
|
Fig. 6 Inverse design compression flow path based on outflow parameter requirements |
在此基础上,为了更贴近工程实际中高超声速进气道的性能需求,文献[17, 18]继续发展了有两道、三道弯曲激波的流场反设计方法。图 7为通过三道弯曲激波实现出口马赫数线性分布的流场反设计结果,图中hexit为出口截面高度,h为与出口截面上与顶板的距离。
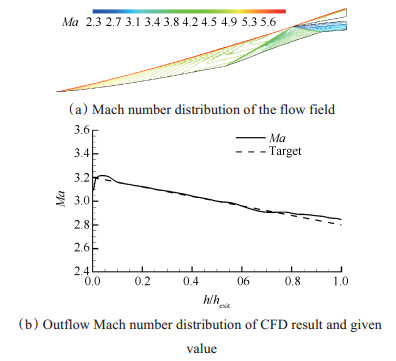
|
Fig. 7 Inverse design achieving uniform outflow using three curved shock waves |
这些流道反设计方法在无粘条件下有良好的效果,而在实际粘性流动中因附面层影响不可避免会偏离设计,甚至会导致进气道无法起动等问题[17],因此对粘性影响的修正方法、以及直接在粘性条件下实现进气道、隔离段反设计的方法值得进一步探索。
三维流场的反设计仍是当前研究的难点之一,文献[17]对此进行了初步研究,通过一系列二维流场积叠形成三维流场,能够近似实现所需的出口截面参数分布。
此外,对于进气道出口参数分布的具体要求,目前尚没有确定的结论,需要在发动机整体设计中协调考虑。
5 根据沿程参数反设计轴对称基准流场为了避免Busemann流场、ICFA流场等传统基准流场的缺点,获得高性能内转进气道基准流场,有必要发展根据沿程气动参数反设计基准流场的新方法。
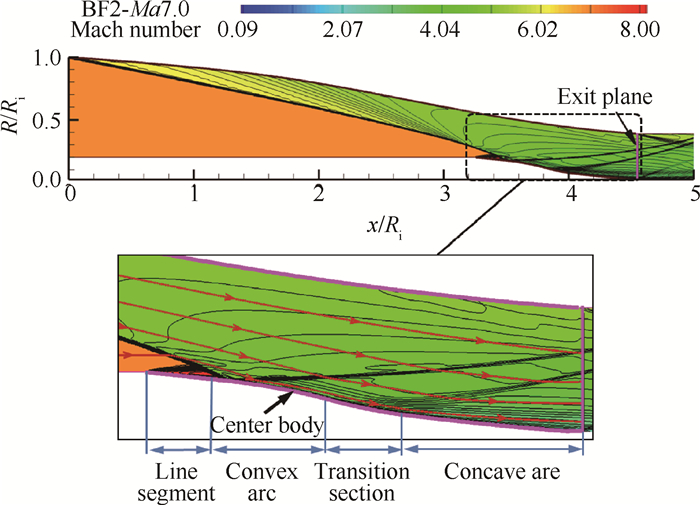
南向军等[19]提出了采用特征线法反设计轴对称基准流场的方法,其基本思想是在传统的特征线法计算过程中,以壁面气动参数的分布规律代替壁面坐标求解方程组,从而直接得到满足气动要求的壁面坐标。文献[20, 21]对多种压力分布进行对比后,提出了初始和末尾部分压升缓、中间压升快这种较为理想的反正切函数形式的压力分布。在此基础上,李永洲等[22, 23]提出了反正切函数形式的沿程马赫数分布,反设计得到的基准流场综合性能有进一步提高,图 8为该流场内及流线上的马赫数分布,Ri为进口半径。可见这是一种典型的轴对称弯曲激波-曲面压缩基准流场。
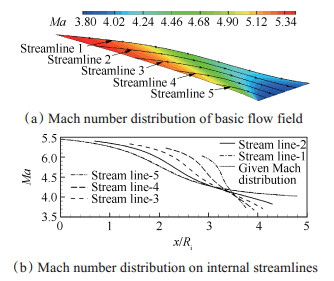
|
Fig. 8 Inward turning inlet basic flow field inverse design according to Mach number distribution |
为了提高基准流场压缩效率并降低进气道内发生附面层分离的可能性,提出了通过改进中心体母线形状从而减弱基准流场反射波强度的方法,例如采用下凹圆弧[24]、上凸-下凹圆弧[25]等形状的中心体母线。图 9为中心体末端采用的上凸-下凹圆弧形状,能够有效减弱反射波,而且能够改进流场在高马赫数来流时的性能。
|
Fig. 9 Structure of basic flow field with center body consisting of convex-concave arc |
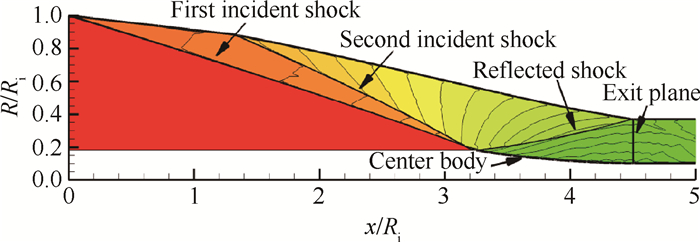
为了进一步改善基准流场的可控性和气动性能,李永洲[26]提出了给定多道激波配置的马赫数分布可控轴对称基准流场的反设计方法,通过同时指定激波强度和压缩面马赫数分布来控制基准流场中激波压缩和等熵压缩的比例。基于此概念,研究了“两波三区”、以及具有双弯曲入射激波的“三波四区”等新型基准流场。图 10为“三波四区”基准流场马赫数分布,其中指定第二道入射激波与反射激波强度相等,因此流场能够达到较高的压缩效率[27]。
|
Fig. 10 Innovative axisymmetric basic flow field containing three shock waves and four regions |
以上反设计研究均针对轴对称基准流场进行,而非轴对称的三维流场反设计仍是目前的难点之一,值得进一步探索。
6 根据壁面参数反设计二元流场与轴对称基准流场的反设计方法相似,在应用特征线法计算二元流场过程中,以壁面气动参数(如压力或速度等)代替壁面坐标求解方程组能够实现二元曲面压缩流场的反设计。另外,还可以直接采用Prandtl-Meyer方程进行近似的反设计[28, 29]。
壁面气动参数变化规律反映了气流的压缩历程,对前缘激波形状、出口流场性能均有决定性的作用,而且壁面压力变化的梯度对附面层的发展也有重要影响。因此根据壁面参数进行反设计有利于更快地寻求满足需要的压缩流场。
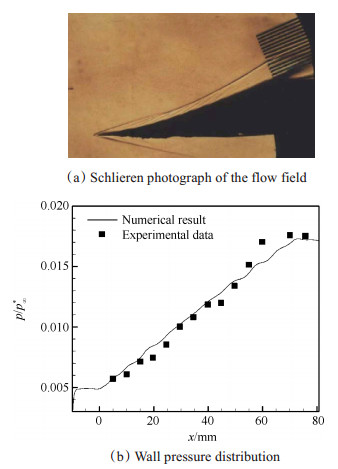
潘瑾详细研究了壁面等压力梯度的曲面压缩流场的流场性能并进行了风洞实验验证[30](见图 11),张林对多种形式的壁面压力、马赫数分布反设计得到的流场性能进行了研究[10],分析了各类参数分布的优缺点。
|
Fig. 11 Experimental investigation of curved shock compression with constant wall pressure gradient |
为了结合优化算法进行自动寻优,文献[9]提出了一种具有通用性和扩展性的设计条件参数化方法,其中以分段的二次Hermite插值函数描述壁面压力分布
| $ \begin{array}{*{20}{l}} {{p_{\bar x}}/{p_\infty } = {{\bar p}_i} + \left( {\bar x - {{\bar x}_i}} \right){{\bar g}_i} + }\\ {\frac{1}{2}{{\left( {\bar x - {{\bar x}_i}} \right)}^2}\left( {{{\bar g}_{i + 1}} - {{\bar g}_i}} \right)/\left( {{{\bar x}_{i + 1}} - {{\bar x}_i}} \right)}\\ {{{\bar x}_i} \le \bar x \le {{\bar x}_{i + 1}}\left( {i = 1, 2, \cdots , N - 1} \right)} \end{array} $ | (1) |
式中
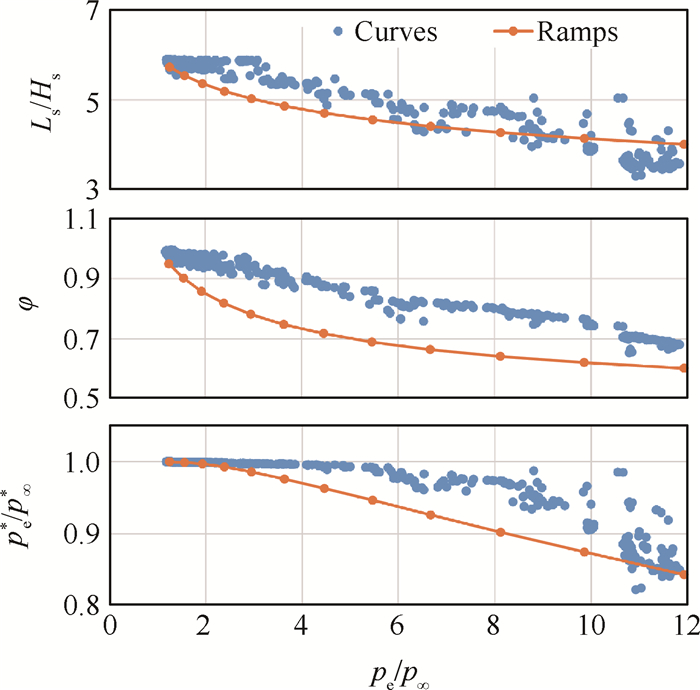
基于此方法的多目标优化设计结果表明,曲面压缩Pareto最优解集中存在长度、压缩效率、低马赫数流量系数等性能参数均优于常规等激波强度三楔压缩的方案[9],如图 12所示,其中Ls,hs分别为激波的长度和高度,φ为来流马赫数4时的流量系数,
|
Fig. 12 Pareto solution of curved shock compression optimization with four objectives |
对于三维型面的设计,李怡庆等[31]通过一系列离散的二维流场积叠实现流向、展向压力分布均可控的三维反设计,莫建伟[32]提出了一种对展向流动进行修正的方法,李大进等[33]、李永洲等[34]尝试了在已有二元基准流场中追踪流线形成三维型面的方法。相关的问题仍值得深入研究,并且有必要探索新的三维反设计方法。此外,粘性条件下的反设计也是目前的难点之一。
7 在进气道/前体设计中的应用对上述反设计方法在各种类型进气道及前体设计中应用的研究,表明了这种压缩方式的优越性。
南向军、李永洲等研究了基于沿程参数可控轴对称基准流场追踪流线设计矩形转圆形内转进气道的方法[20, 26],同时研究了改善其起动性的措施[35],风洞试验表明所设计的进气道性能达到了较高水平[36],见表 1。
|
|
Table 1 Inlet performance at Ma∞=6, α∞=4° |
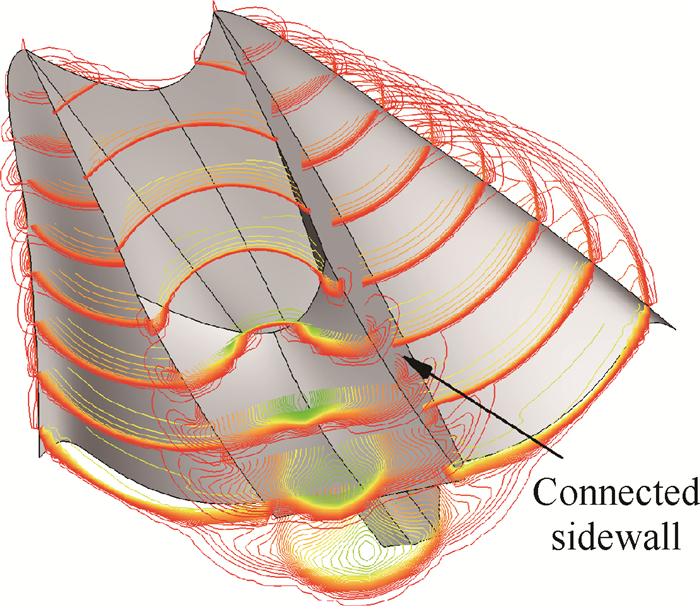
进气道必须与前体一体化已成为高超声速飞行器设计中的共识,基于曲面压缩概念已提出了多种的进气道/前体一体化方法,并且相关问题仍是研究热点之一[37, 38]。李永洲应用马赫数分布可控的外锥形和内锥形基准流场,提出了一种内外双乘波的一体化设计方案(图 13),构型容积率较高并具有良好的气动性能[26]。李怡庆等以二元弯曲激波进气道为基础,发展了一种横向压力可控的进气道/前体一体化乘波设计,性能优于常规的楔导乘波一体化方案[31]。
|
Fig. 13 Wave structure of dual-waverider integrated forebody and inward turning inlet |
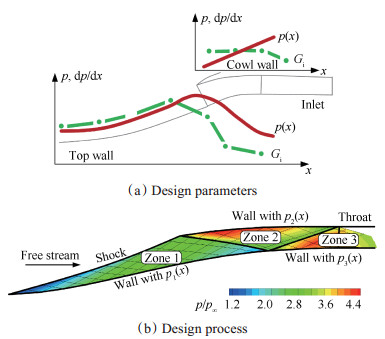
文献[39]将二元曲面压缩流场反设计方法发展到二元进气道内压缩段,提出了串联组合多个曲面压缩流场形成高超声速压缩系统的方法(图 14),从而实现了二元弯曲激波进气道全流道整体反设计。采用这种设计方法结合多目标优化算法,能够获取综合性能较好的进气道方案。这是一种物理意义明确、真正意义上的气动设计而非几何设计。
|
Fig. 14 Integrated inverse design method of 2D inlet external and internal compression based on given pressure distribution |
另外,侧压式进气道顶板与侧板[40, 41]、轴对称进气道中心锥[42]设计中采用曲面压缩的概念均取得了较好的效果。
综合来看,在高超声速推进系统设计中采用曲面压缩的理念能够为其性能带来进一步提升。
8 柔性变几何概念高超声速进气道需要在较宽的马赫数范围内均保持尽量高的压缩能力和压缩效率,同时又要避免低马赫数飞行时难以起动的问题,采用变几何设计是最根本的解决途径。对于曲面压缩方式,通过使进气道顶板的弯曲型面随飞行马赫数的变化而变形,从而灵活地控制外压段弯曲激波的位置,无疑是很有吸引力的设计思想。
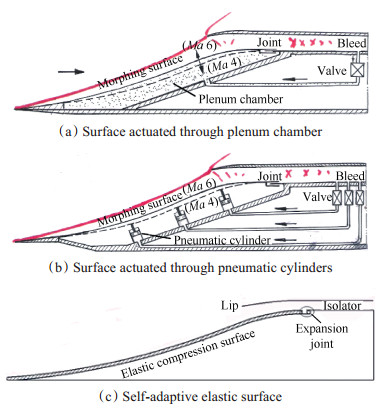
文献[43~46]研究了多种基于曲面压缩的柔性自适应变几何进气道概念(图 15),并通过流固耦合计算和风洞实验,初步分析了其可行性和设计方法。这种新型设计概念值得进一步进行计算分析和实验研究。
|
Fig. 15 Conceptual designs of inlet with morphing compression surface |
图中三种构思均可随马赫数变化实现弯曲激波形态的控制。
9 曲面压缩概念的拓展必须说明,文章介绍的曲面压缩概念可以拓展为可控气动参数的曲面膨胀概念。曲面压缩所采用的研究方法不仅可以应用于高速气流的压缩过程设计,同样也适用于高速气流膨胀过程的设计,实现高速气流流道有明确物理意义的气动设计而非几何设计。
随着采用吸气式发动机高超声速技术的发展,一种新的评价压缩面对气流压缩效率的参数——暂且取名为“面压效率比”Ks
| $ {K_{\rm{s}}} = \frac{{\pi \cdot \sigma }}{{S \cdot \dot m}} $ | (2) |
式中
文章回顾、总结了曲面压缩流场相关的研究成果,包括其流场特征、设计方法、在进气道中的应用等,并展望了曲面压缩进一步发展的可能性,研究表明:
(1) 超声气流曲面压缩是一种让全部压缩表面都参与对气流压缩的压缩方式。
(2) 曲面压缩通过可控的弯曲激波和可控的等熵压缩相互配合的压缩方式完成对超声/高超声速气流的压缩。其独特的压缩方式,有别于一般的多级平面斜楔压缩和常规的等熵压缩。
(3) 计算和实验研究证明了曲面压缩的良好气动性能,为高性能高超声速进气系统或者排气系统的气动设计提供了全新的方法。
(4) 曲面压缩的概念还有巨大的发展空间。总体看来,在三维曲面压缩流场的反设计、考虑粘性的反设计等方面迫切需要创新的构思和创新的解决方案。随着曲面压缩研究的深入,必然出现不少空白的气动-热力难点有待深入探索和研究。
(5) 提出了一种新的评价压缩面对气流压缩效率的参数——“面压效率比”Ks,可以用于动力总体和飞行器总体评价进气道的气动设计水平,也是衡量进气道自身性能的一个有用指标。
致谢 本文初稿由王磊博士整理,本人深表谢意。
| [1] |
Heiser W H, Pratt D T. Hypersonic Airbreathing Propulsion[M]. Reston: AIAA Education Series, 1994.
(  0) 0) |
| [2] |
Curran E T, Murthy S N B. Scramjet Propulsion[M]. Reston: AIAA Progress in Acstronautics and Aeronautics, 2000.
(  0) 0) |
| [3] |
王振国, 梁剑寒, 丁猛, 等. 高超声速飞行器动力系统研究进展[J]. 力学进展, 2009, 39(6): 716-739. DOI:10.3321/j.issn:1000-0992.2009.06.011 (  0) 0) |
| [4] |
Zhang K Y. Research Progress of Hypersonic Inlet Inverse Design Based on Curved Shock Compression System[R]. AIAA 2015-3647.
(  0) 0) |
| [5] |
王磊.高超声速二元弯曲激波压缩流场的分析、优化与应用[D].南京: 南京航空航天大学, 2016.
(  0) 0) |
| [6] |
M lder S. Lecture on Curved Aerodynamic Shock Waves[C]. Xiamen: Summer School Lecture on Hypersonic Propulsion Technology, 2014.
(  0) 0) |
| [7] |
Emanuel G. Shock Wave Dynamics Derivatives and Related Topics[M]. Boca Raton: Taylor & Francis, 2013.
(  0) 0) |
| [8] |
韩伟强, 朱呈祥, 尤延铖, 等.二阶弯曲激波理论的推导与应用研究[C].哈尔滨: 第八届全国高超声速科技学术会议论文摘要集, 2015.
(  0) 0) |
| [9] |
王磊, 张堃元, 苏纬仪, 等. 高超声速二元弯曲激波压缩流场性能分析[J]. 推进技术, 2017, 38(4): 764-771. (WANG Lei, ZHANG Kun-yuan, SU Wei-yi, et al. Performance Analysis of Hypersonic 2D Curved Shock Compression Flow Field[J]. Journal of Propulsion Technology, 2017, 38(4): 764-771.)
(  0) 0) |
| [10] |
张林.等熵压缩波分散交汇的超/高超声速曲面压缩系统研究[D].南京: 南京航空航天大学, 2014.
(  0) 0) |
| [11] |
居燕.弯曲激波压缩面设计及试验研究[D].南京: 南京航空航天大学, 2005.
(  0) 0) |
| [12] |
潘瑾.超声/高超声速非均匀来流下曲面压缩系统研究[D].南京: 南京航空航天大学, 2011.
(  0) 0) |
| [13] |
方兴军.控制出口速度分布的超声速内流通道反设计[D].南京: 南京航空航天大学, 2012.
(  0) 0) |
| [14] |
Fang X J, Zhang K Y. Inverse Design of Supersonic Internal Flow Path Based on Given Outflow Velocity Profile[R]. AIAA 2012-4064.
(  0) 0) |
| [15] |
韩伟强, 朱呈祥, 尤延铖, 等. 给定下游边界的超声速流场逆向求解方法[J]. 推进技术, 2016, 37(4): 624-631. (HAN Wei-qiang, ZHU Cheng-xiang, YOU Yan-cheng, et al. An Inverse Method for Supersonic Flowfield with Given Downstream Boundary[J]. Journal of Propulsion Technology, 2016, 37(4): 624-631.)
(  0) 0) |
| [16] |
郭善广, 王振国, 赵玉新, 等. 高超声速二元进气道前体曲线激波逆向设计研究[J]. 航空学报, 2014, 35(5): 1246-1256. (  0) 0) |
| [17] |
刘燚.控制出口马赫数分布的高超声速压缩通道反设计[D].南京: 南京航空航天大学, 2012.
(  0) 0) |
| [18] |
钟启涛, 张堃元, 庞丽娜. 出口马赫数分布可控的二元高超进气道双重反设计[J]. 推进技术, 2015, 36(7): 982-988. (ZHONG Qi-tao, ZHANG Kun-yuan, PANG Li-na. Double Inverse Design of 2-D Hypersonic Inlet with Controllable Exit Mach Number Distribution[J]. Journal of Propulsion Technology, 2015, 36(7): 982-988.)
(  0) 0) |
| [19] |
南向军, 张堃元, 孙波.压缩面升压规律可控的高超进气道轴对称基准流场设计方法研究[C].北京: 中国航空学会航空动力分会火箭发动机专业委员会2009年推进技术学术年会, 2009.
(  0) 0) |
| [20] |
南向军.压升规律可控的高超声速内收缩进气道设计方法研究[D].南京: 南京航空航天大学, 2012.
(  0) 0) |
| [21] |
Nan X J, Zhang K Y. Numerical and Experimental Investigation on Hypersonic Inward Turning Inlets with Basic Flowfield Using Arc Tangent Curve Law of Pressure Rise[R]. AIAA 2011-2270.
(  0) 0) |
| [22] |
李永洲, 张堃元, 南向军. 基于马赫数分布规律可控概念的高超声速内收缩进气道设计[J]. 航空动力学报, 2012, 27(11): 2484-2491. (  0) 0) |
| [23] |
Li Y Z, Zhang K Y. Design of Hypersonic Inward Turning Inlets with Controllable Mach Number Distribution[R]. AIAA 2012-4151.
(  0) 0) |
| [24] |
南向军, 张堃元. 采用新型基准流场的高超声速内收缩进气道性能分析[J]. 宇航学报, 2012, 33(2): 254-259. DOI:10.3873/j.issn.1000-1328.2012.02.016 (  0) 0) |
| [25] |
李永洲, 张堃元, 钟启涛. 四段修型弥散反射激波中心体基准流场研究[J]. 航空动力学报, 2014, 29(9): 2055-2062. (  0) 0) |
| [26] |
李永洲.马赫数分布可控的高超声速内收缩进气道及其一体化设计研究[D].南京: 南京航空航天大学, 2014.
(  0) 0) |
| [27] |
李永洲, 张堃元, 朱伟, 等. 双弯曲入射激波的可控中心体内收缩基准流场设计[J]. 航空动力学报, 2015, 30(3): 563-570. (  0) 0) |
| [28] |
Emanuel G. Supersonic Compressive Ramp Without Laminar Boundary-Layer Separation[J]. AIAA Journal, 1984, 22(1): 29-34. DOI:10.2514/3.48415
(  0) 0) |
| [29] |
潘瑾, 金峰, 张堃元. 非均匀来流下等压力梯度曲面压缩系统的试验研究[J]. 推进技术, 2013, 34(12): 1593-1600. (PAN Jin, JIN Feng, ZHANG Kun-yuan. Experimental Investigation of Constant Pressure Gradient Curved Compression System in Non-Uniform Inflow[J]. Journal of Propulsion Technology, 2013, 34(12): 1593-1600.)
(  0) 0) |
| [30] |
Pan J, Zhang K Y. Experimental and Numerical Investigation of a Curved Compression System Designed on Constant Pressure Gradient[R]. AIAA 2009-5270.
(  0) 0) |
| [31] |
李怡庆, 韩伟强, 尤延铖, 等. 压力分布可控的进气道/前体一体化乘波设计[J]. 航空学报, 2016, 37(9). (  0) 0) |
| [32] |
莫建伟. TBCC排气系统设计方法及流场特性研究[D].南京: 南京航空航天大学, 2015.
(  0) 0) |
| [33] |
李大进, 高雄, 朱守梅. 弯曲激波压缩曲面的二元高超声速进气道研究[J]. 推进技术, 2013, 34(11): 1441-1447. (LI Da-jin, GAO Xiong, ZHU Shou-mei. Study of Hypersonic 2D-Inlet with Leading Curved-Shock Wave Compression Ramp[J]. Journal of Propulsion Technology, 2013, 34(11): 1441-1447.)
(  0) 0) |
| [34] |
李永洲, 张堃元, 王磊, 等. 基于二维曲面基准流场的流线追踪高超声速进气道设计[J]. 航空动力学报, 2012, 27(9): 2004-2012. (  0) 0) |
| [35] |
李永洲, 张堃元, 张留欢. 抽吸对高超声速内收缩进气道涡流区及起动性能的影响[J]. 航空动力学报, 2016(7): 1630-1637. (  0) 0) |
| [36] |
南向军, 张堃元, 金志光. 采用新型基准流场的高超内收缩进气道试验研究[J]. 航空学报, 2014, 35(1): 90-96. (  0) 0) |
| [37] |
尤延铖, 梁德旺, 郭荣伟, 等. 高超声速三维内收缩式进气道/乘波前体一体化设计研究评述[J]. 力学进展, 2009(5): 513-525. DOI:10.3321/j.issn:1000-0992.2009.05.001 (  0) 0) |
| [38] |
吴颖川, 贺元元, 贺伟, 等. 吸气式高超声速飞行器机体推进一体化技术研究进展[J]. 航空学报, 2015, 36(1): 245-260. (  0) 0) |
| [39] |
王磊, 张堃元, 金志光, 等. 基于壁面压力分布的二元高超声速弯曲激波压缩进气道反设计与优化方法[J]. 推进技术, 2013, 34(12): 1601-1605. (WANG Lei, ZHANG Kun-yuan, JIN Zhi-guang, et al. Reverse Design and Optimization of 2D Hypersonic Curved Shock Compression Inlet Based on Given Wall Pressure Distribution[J]. Journal of Propulsion Technology, 2013, 34(12): 1601-1605.)
(  0) 0) |
| [40] |
Zhang L, Zhang K Y, Wang L. Application Study of the Curved Surface Compression System in Three-Dimensional Sidewall Compression Inlet[R]. AIAA 2014-2840.
(  0) 0) |
| [41] |
刘辰昊.壁面参数融合可控的高超侧压式进气道初步研究[D].南京: 南京航空航天大学, 2015.
(  0) 0) |
| [42] |
向有志, 张堃元, 王磊, 等. 壁面压升可控的高超轴对称进气道优化设计[J]. 航空动力学报, 2011, 26(10): 2193-2199. (  0) 0) |
| [43] |
杨顺凯, 张堃元, 王磊. 高超可调进气道弹性压缩面自适应无源控制概念研究[J]. 推进技术, 2015, 36(11): 1633-1639. (YANG Shun-kai, ZHANG Kun-yuan, WANG Lei. Research on Self-Adaptive and Passivity-Based Control Concept of Hypersonic Adjustable Inlet with Elastic Compression Surface[J]. Journal of Propulsion Technology, 2015, 36(11): 1633-1639.)
(  0) 0) |
| [44] |
杨顺凯, 张堃元, 王磊, 等. 多点集中力下高超进气道弹性变几何研究[J]. 航空动力学报, 2015, 30(10): 2516-2522. (  0) 0) |
| [45] |
杨顺凯, 张堃元, 王磊, 等. 流量系数可控弹性自适应高超进气道研究[J]. 推进技术, 2014, 35(12): 1592-1597. (YANG Shun-kai, ZHANG Kun-yuan, WANG Lei, et al. Research on Elastic and Self-Adaptive Hypersonic Inlet with Controllable Flow Coefficient[J]. Journal of Propulsion Technology, 2014, 35(12): 1592-1597.)
(  0) 0) |
| [46] |
甘宁钢.宽马赫数凹曲激波压缩进气道型面变几何研究[D].南京: 南京航空航天大学, 2012.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

