2. 中国航发沈阳发动机研究所,辽宁 沈阳 110015
2. AECC Shenyang Engine Institute, Shenyang 110015, China
霍尔推力器是一种电磁式加速推进装置[1],通过电离中性气体,喷射高速离子形成反向推力[2]。与化学推进相比,霍尔推力器具有高比冲、长寿命、高有效载荷率等特点,已被各国广泛应用于航天领域[3]。
全电推卫星代表了当前最先进的卫星技术。它要求电推力器除了完成卫星在轨的南北位保任务之外,还需在之前的卫星转轨阶段完成轨道提升的任务。功能的更新颠覆了霍尔推力器的工作模式。卫星南北位保所需任务速度小,霍尔推力器每次启动只需要连续工作约1h,远不到其热稳定时间(3.5~ 4h)。轨道提升相较于南北位保所需的任务速度大大增加,为了缩短任务周期,要求霍尔推力器必须长时间连续工作[4],于是其工作模式由非热稳态转向了热稳态。热稳态工作引起的推力器零部件温度的变化要远大于非热稳态工作引起的变化[1];因此,高温放电稳定性是对霍尔推力器技术发展提出的新要求。
作者所在研究团队在开展基于全电推卫星需求的霍尔推进技术的研究过程中发现,推力器在某些工况下出现了放电通道壁面过热、放电电流随时间增长越来越快的热失稳现象。此外,国际同行在报道大功率霍尔推力器研制情况时已经明确指出推力器的热管理及热防结构设计很重要[5, 6];然而,可能是出于技术保密的原因,没有透露更多的细节。综合来看,推力器零部件的热状态与放电稳定性之间联系紧密。
磁路是霍尔推力器结构中最重要的组成部分,用来产生推力器正常放电所需的磁场。kW功率量级以上的推力器一般使用电工纯铁等软磁材料结合通电线圈的励磁方式。众所周知,磁性材料的铁磁性受温度影响,会随着温度的升高而减弱;当达到居里温度时,铁磁性会完全消失。由此推测,一方面,推力器放电功率在通道壁面沉积使得磁路温度升高,励磁能力下降,通道内磁场减弱;另一方面,通道内磁场强度的下降影响了放电过程以及壁面功率沉积。这其中存在放电特性与材料特性之间的交互影响。然而,两者之间是否存在正反馈机制从而导致推力器发生放电热失稳则有待更加深入的研究。
目前并没有公开发表的文献报道与放电热稳定性相关的基础研究。人们更多地关注霍尔推力器通道内放电产生的等离子体对推力器壁面的传热特性,并在放电功率、放电电压以及磁场等因素影响通道壁面功率沉积以及温度分布等方面开展了大量的研究工作[7~13];此外,对推力器在不同工作环境下进行热分析与测试研究有助于评估其工作可靠性,兰州空间技术物理研究所对此开展了相关研究[14, 15]。在温度对霍尔推力器磁路及通道内磁场的影响方面,法国Vial V等[16]模拟了永磁铁磁路推力器PPS1350在293K和750K条件下通道内的磁场,结果表明最大磁场强度在高温下减弱了10%;不过在软磁构型中,磁场强度在750K时仅比在293K时低2%~3%,且磁场位型变化不大。哈尔滨工业大学测量了电工纯铁软磁材料在不同温度下的B-H曲线[17]。研究发现,当磁路温度从20℃增加到500℃时,B-H曲线饱和段的磁导率下降了约16%。
基于上述分析与调研,本文提出对磁路温度影响霍尔推力器放电热稳定性的问题开展研究,旨在明确推力器放电与磁路材料属性变化之间的交互影响过程,搞清楚交互影响的反馈性质,确定其对放电热失稳的贡献。
2 霍尔推力器中的放电热失稳霍尔推力器的放电热失稳现象具体表现为:随着放电的进行,放电电流会逐渐上升,且上升速率越来越快;与此同时,肉眼可以观测到放电通道壁面由不发光逐渐开始发红光,且亮度越来越高,图 1为熄火瞬间捕捉到的陶瓷管整体呈红色。在这个过程中,没有对推力器的任何可控参数进行任何调整,因此放电电流增长速率越来越大的现象可以认定为放电失稳;与放电失稳过程在表象上相呼应的便是放电通道由正常的暗色(低温)变成过热的亮红色(高温)的非热平衡过程。这两个过程相互伴生,是为放电热失稳。

|
Fig. 1 Ceramic tube overheating shot after Hall thruster shutdown |
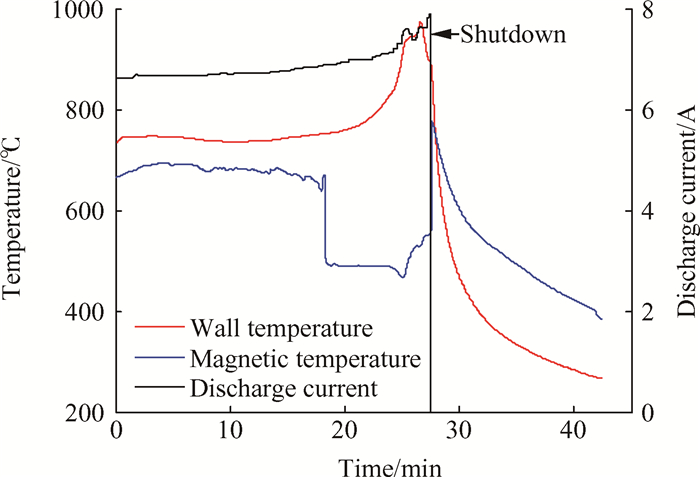
图 2是霍尔推力器发生放电热失稳的过程实例。此时霍尔推力器工作在放电电压700V、阳极氙气流量70sccm的工况下,属于高电压、大功率范畴。推力器在此工况下准稳态工作了近20min;在这个阶段,放电电流、外壁面温度(约750℃)和内磁屏温度(约680℃)几乎不变或缓慢增长。然而,在接下来的10min里推力器发生了失稳;放电电流和壁面温度快速上升,在强制关机的时刻,壁面温度达到了将近1000℃。由于失稳过程同时伴随放电振荡的加剧,从而对金属属性的内磁屏的测温信号造成了干扰,导致数据异常;不过在关机瞬间,由于干扰消失,仍然捕捉到了此时内磁屏的温度在780℃左右。
|
Fig. 2 Parameter evolution of unstable discharge of certain Hall thruster |
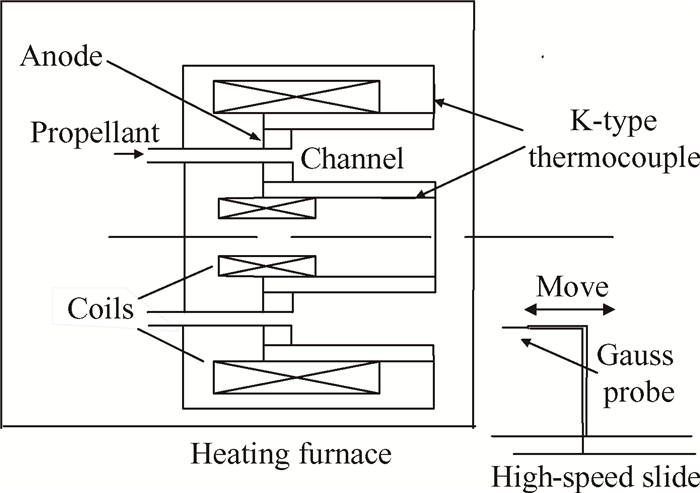
为了能够直接测量高温磁路下放电通道内的磁场分布,设计了如图 3所示的实验方案。实验设备主要包括一台霍尔推力器、一台常压加热炉、一台测量磁场用的高斯计及配套的霍尔探头、一套伺服电机驱动的高速滑台以及一台数据采集计算机。霍尔推力器置于加热炉内,调节加热炉的目标温度参数可以使得推力器磁路到达不同的温度。霍尔探头固定在高速滑台上;当磁路被加热到目标温度之后,伺服电机驱动霍尔探头沿着轴向快进快出推力器的放电通道测量磁场,并规避高温辐射对霍尔探头测量的影响。霍尔探头的测量结果被实时传输到高斯计中,然后通过串口通信同步传输到数据采集计算机上实现数据存储。为了更加真实地反映测量过程中的磁路温度,分别在霍尔推力器的内磁屏表面以及外磁极端面布置了两根K型热电偶。
|
Fig. 3 Schematic diagram of experiment setup |
实验使用的霍尔推力器是作者所在团队自行设计的型号为P100的原理样机。P100的通道外径为100mm,通道宽度为15mm,与SPT-100相当[18]。P100通道中的磁场是软磁磁路和绕制线圈共同产生。实验中利用一50V、10A的直流稳压电源为线圈供电。此外,实验只测量了放电通道中心线上的磁场强度分布;为此,调节了高斯探头的高度,使其与P100的通道中心线水平。
高斯计的型号为CH-1500,霍尔探头的型号为MCHD800F,由北京翠海佳诚磁电科技有限责任公司提供。此型号高斯计最大测量磁场强度为3T,分辨率为0.1G,满足测试要求。此型号霍尔探头的感应元件是横向的,通过合理摆放可测量得到霍尔推力器通道内磁场的最主要分量——径向磁感应强度。
为了较全面地反映磁路在高温下的励磁能力,实验中分别测量了当磁路在室温下处于线性励磁区以及饱和励磁区时径向磁感应强度的轴向分布。
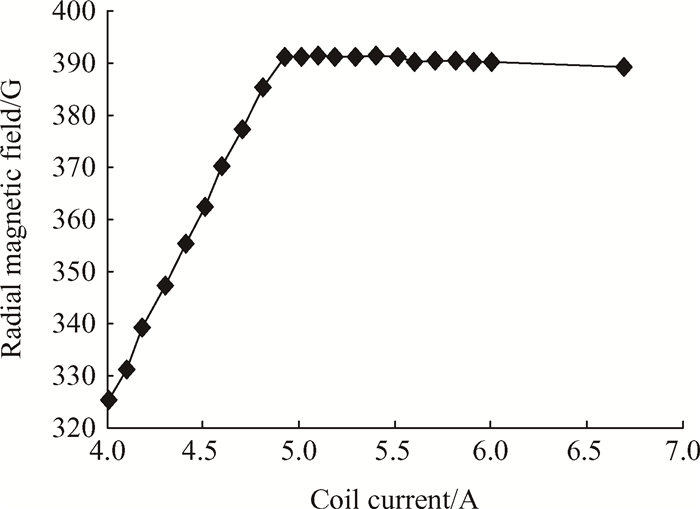
3.2 实验结果分析图 4是在不同线圈电流下测量得到的P100推力器内壁面出口处的径向磁场强度曲线。可见,随着线圈电流的不断增加,磁感应强度首先线性增长;当线圈电流大于5A之后,磁感应强度保持不变,甚至有些许降低。因此,P100磁路具有很明显的饱和励磁特征。当线圈电流小于5A时,P100磁路处于线性励磁区;当线圈电流大于5A时,P100磁路处于饱和励磁区。霍尔推力器的励磁工作点一般应选择在线性励磁区,且远离饱和转变点,以保持对推力器的调控能力。在这里,为了达到实验目的,分别选择了线圈电流为4A(线性区)和6A(饱和区)的情况测量了不同磁路温度下的磁场分布。
|
Fig. 4 Variation of radial magnetic field at the exit of inner wall with coil current |
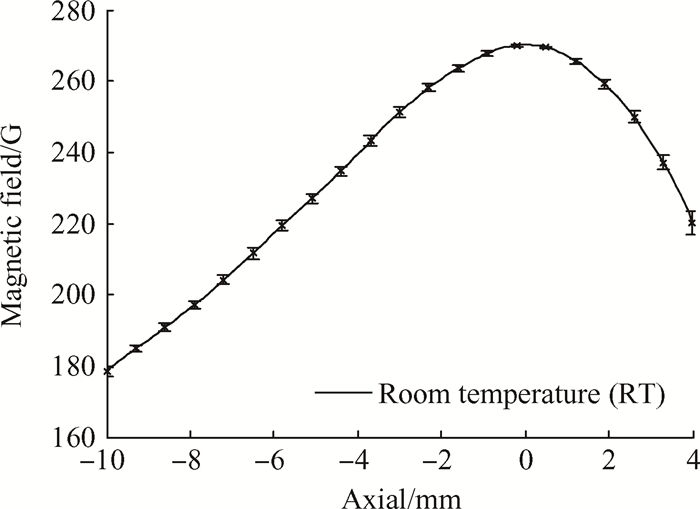
由于霍尔探头在伺服电机的驱动下高速往返完成测量,因此其可能会受到加减速惯性等因素影响而来回振动,从而增加测量结果的不确定度。图 5给出了在室温条件下当线圈电流为6A时多次测量通道中心线上径向磁场强度分布的统计结果。通过图中误差杆的长度可知,高速驱动下的霍尔探头具有较高的测量稳定性,测量结果的重复性很好;因此这种驱动方法是有效的。
|
Fig. 5 Uncertainty assessment of high-speed measurement at a coil current of 6A |
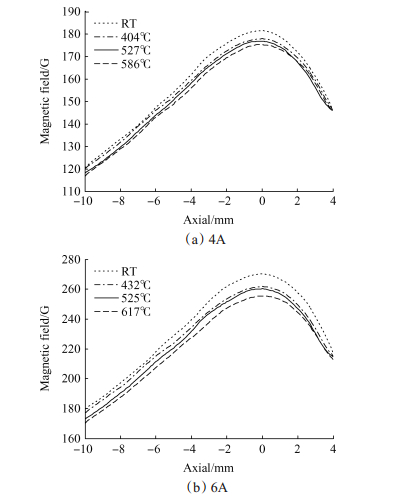
图 6是不同温度下P100推力器线性磁路(线圈电流为4A)与饱和磁路(线圈电流为6A)产生的磁场分布的测量结果。首先可以看出,随着磁路温度的升高,磁感应强度呈总体单调下降的趋势,这符合铁磁材料的特性;由这个规律可以推测,磁场位型应该变化不大,这与文献[16]的结果吻合。其次,线性磁路与饱和磁路在高温下励磁性能的衰减程度相差不大。当内磁屏的温度从室温升高到600℃左右时,线性磁路在通道中心线上产生的最大径向磁感应强度从181.5G减小到了175.3G,相对变化量为3%;而饱和磁路在通道中心线上产生的最大径向磁感应强度从270.3G减小到了255.3G,相对变化量为5%。两者基本相当;因此,温度对磁路励磁能力的影响与磁路是否处于饱和的状态关系不大。上述发现同时说明,即使是在600℃的高温状态下,磁路材料的励磁能力并没有显著衰减。联系到图 2给出的信息,当内磁屏的温度达到650℃以后,推力器仍然稳定工作了一段时间直至失稳,这或许印证了本实验得到的在600℃以下磁路励磁性能衰减较小的测量结果是可信的。
|
Fig. 6 Measured distribution of magnetic field intensity under different coil currents and magnetic circuit temperature |
考虑到纯铁材料完全消磁的居里温度约为770℃,而本实验的研究表明即使在600℃下,磁场强度才发生了约5%的衰减,因此可以断定,磁路温度对推力器通道内磁场强度衰减的影响不是线性的,而是存在一个非线性加剧的过程。
4 磁路温度影响霍尔推力器放电热稳定性的数值模拟 4.1 数值模型及方法本文采用一个基于Particle-in-Cell(PIC)技术的2D3V模型来仿真霍尔推力器放电通道内等离子体与壁面之间的宏观相互作用,以此来推演放电与热之间的耦合关系。总的来说,将工质原子、离子以及电子均当作离散的个体粒子,然后利用PIC数值方法求解粒子的运动与场的分布,进而统计获得推力器的放电特征。由于推力器的结构是轴对称的,因此假设放电参数以及组件温度都是周向均匀的,将数值模型建立在轴向(z)与径向(r)的二维平面上。本研究小组早已开发了二维PIC模拟平台[19]。该平台经过验证,在霍尔推力器宏观放电及微观机理研究方面均有成功应用[20, 21]。
虽然热失稳问题在某一特定的推力器原理样机上被发现,然而其蕴藏的物理规律却具有一般性。因此,本文选择P100推力器(在第3部分测量磁场用)作为模拟对象。
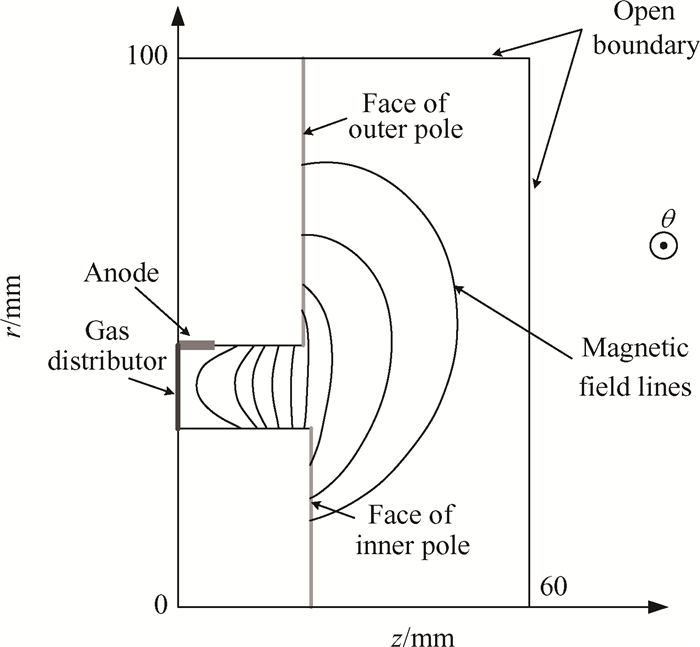
模拟区域的设置及相关尺寸如图 7所示。通道内左边界为气体分配器边界,推进剂原子以半麦克斯韦分布从该边界进入放电通道;此外,分配器处于悬浮状态,其金属表面沉积电荷,可看作电容,电势由ϕ=Q/C计算得到,其中Q为表面沉积的净电荷数;C为电容,假设其值为1×10-8F通道内靠近气体分配器的上边界为阳极边界,电子在该边界被导走形成放电电流,边界电势的大小等于放电电压值。除阳极之外,通道内的上下边界为绝缘壁面边界。霍尔推力器一般采用BN-SiO2陶瓷作为壁面材料,需要考虑入射电子撞击壁面打出二次电子的效应,二次电子发射模型参考文献[21]。此外,绝缘壁面的电势是悬浮的,其上的法向电场采用En=-σ/2ε0求解,其中σ为壁面上沉积的净电荷密度,ε0为真空介电常数。通道外的左边界是内外磁极端面。由于是金属导体材料且处于悬浮状态,因此将其当作电容边界,电势求解方法同气体分配器边界。通道外的下边界为推力器轴线,粒子在这里被镜面反射,其上的电场等于0。通道外的上边界与右边界是开放边界,所有种类的粒子穿过这两个边界后消失。此外,边界电势设置为0;在边界网格上会强制补充电子以保持边界的电中性,类似于阴极的中和作用。原子与固体边界碰撞之后其能量被完全回收,然后以固体边界温度为特征的半麦克斯韦分布重新回到计算区域。离子与所有固体边界碰撞之后都会复合成原子,其能量交换模型来自于文献[22]。
|
Fig. 7 Schematic diagram of simulation domain |
原子的流动按照自由分子流处理。电子在磁场中被磁化,需同时考虑磁场和电场的作用。离子不被磁化,只考虑电场力的作用。模型考虑了电子与原子之间的碰撞,其形式包括弹性碰撞、一价电离碰撞和激发碰撞。推进剂选择为Xe,其碰撞截面的选取见文献[23]。除此之外,模型还考虑了一种电子的Bohm碰撞,用来体现反常传导效应。当Bohm碰撞发生时,电子在推力器的轴向与周向平面内被弹性散射。Bohm碰撞频率为νB=CBeB/me,其中CB为半经验Bohm系数。其它类型的粒子碰撞暂时没有考虑。
模拟区域采用矩形网格划分。由于放电引起的感应磁场很小,因此可以认为磁场是常数,只由磁路励磁产生。此外,由于磁场是静态的,因此电势分布可以通过求解Poisson方程得到,采用有限体积法对Poisson方程进行了离散,求解算法选用文献[24]提出的Dynamic Alternating Direct Implicit(DADI)方法。粒子之间的碰撞采用文献[25]提出的基于Null collision的MCC方法处理。
磁路温度效应主要体现在对磁场的影响上。结合第3部分以及文献[16]的研究结果,可以假设磁路温度不影响通道内磁场位形,只影响整体的强度。然而,由于缺少完备的实验数据,模拟时磁场数据来自于利用FEMM软件对P100推力器的磁路结构进行的建模仿真;而且,通过同等比例改变FEMM软件参数设置里的线圈电流大小,实现磁场强度的整体变化,表征磁路温度的效应。线圈电流越小,磁场强度越小,表征了磁路温度越高。模拟中分别使用了线圈电流为4A,3.5A,3A,2.5A以及2A等5种情况下的磁场,其中4A是P100推力器正常工作的励磁点。为了量化磁路温度效应,这里定义了磁路温度因子χ,它是推力器通道中心线上最大磁场强度在不同线圈电流下相对于4A线圈电流下的相对变化量。χ越大,则磁路温度越高;表 1给出了相关信息。由第3部分的研究结果可知,随着磁路温度的增大,χ的增长会越来越快。
|
|
Table 1 Quantitative representation of magnetic circuit temperature effect |
一些其他的模拟参数设置如下。放电电压为300V,阳极供气流量为5mg/s,阳极温度为800K,内外通道壁面温度为700K,磁极端面温度为500K。半经验Bohm系数CB在通道内外分别为1/160以及1/16。
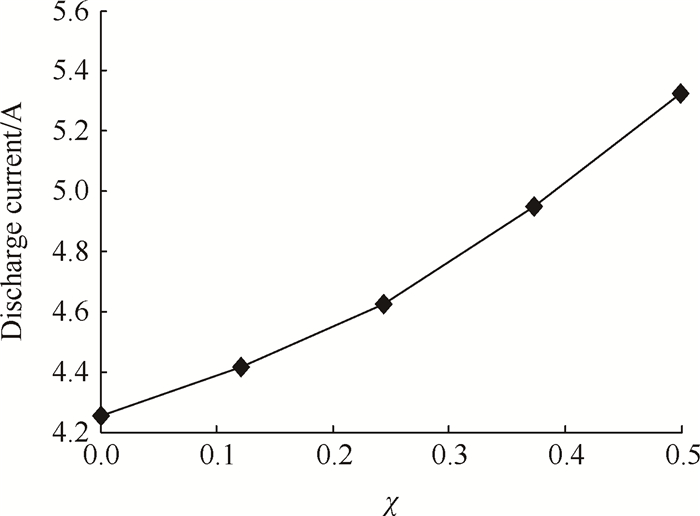
4.2 模拟结果与分析 4.2.1 磁路温度变化与放电特性变化的交互影响关系图 8是模拟得到的放电电流随着磁路温度因子的变化曲线。可见,随着磁路温度的升高(即磁路温度因子χ的增大),放电电流逐渐增大,且呈现增长速率越来越快的趋势,这符合图 2放电热失稳过程中放电电流的变化特征。
|
Fig. 8 Discharge current versus magnetic temperature factor |
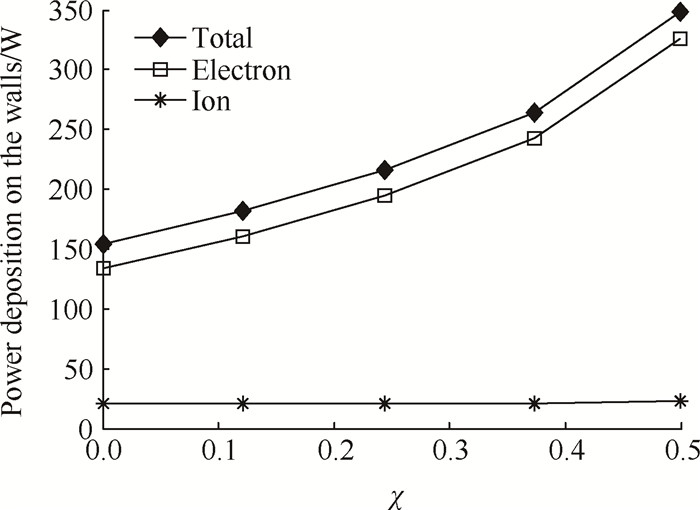
图 9是模拟得到的壁面功率沉积随磁路温度因子的变化曲线。可见,随着磁场强度的变小(即磁路温度因子χ的增大),壁面上沉积的等离子体功率均单调增大,且同样存在增长速率越来越快的趋势,由此推断壁面温度的增长速率也是越来越快的,这符合放电热失稳过程中壁面温度的变化特征。在霍尔推力器特定的磁路结构下,磁路温度与壁面温度正相关;因此,磁路温度随着通道内磁场强度的变小也在非线性增长。
|
Fig. 9 Power deposition on the walls versus magnetic temperature factor |
综上可以确定,通过壁面这一中间纽带,磁路温度变化与放电等离子体特性变化之间存在正反馈效应:当霍尔推力器放电工作时,磁路被加热升温,于是其励磁能力下降,产生的磁场强度减弱。磁场强度的衰减影响了通道内等离子体的放电行为,使得等离子体沉积在通道壁面的功率损失增大,损失进一步转变为热使磁路升温,由此形成了正反馈过程。
霍尔推力器组件的温度取决于产热与散热两方面。放电等离子体是最主要的产热源;而推力器向环境的辐射是最重要的散热手段。若推力器的散热能力不足,无法平衡等离子体放电在壁面上的产热,那么磁路温度会越来越高,进而出现如图 2所示的热失稳现象。因此,只有当散热能力等于或超过产热能力时,由于磁路温度效应引起的热失稳现象才能被避免。
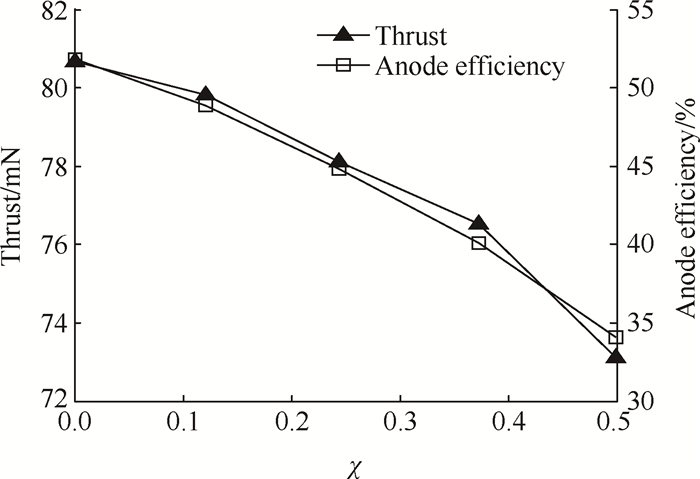
更进一步,霍尔推力器的散热能力应该越强越好。这是因为磁路温度的升高同时破坏了推力器的性能表现。图 10给出了模拟得到的推力器性能随磁路温度因子变化的结果。可见,随着磁路温度因子的增大,推力与效率均单调加速下降。因此,为了得到具有较高性能的霍尔推力器,磁路温度应该越低越好,这就对霍尔推力器的热设计提出了要求。考虑到本文实测在600℃的温度以下,推力器磁材料的励磁能力衰减很小,不到5%,结合图 10可见,性能衰减的比例很小。因此,在进行霍尔推力器热设计时将磁路温度控制在600℃以下对于性能设计而言是可以接受的。
|
Fig. 10 Performance parameters versus magnetic temperature factor |
从上面的分析中可知,磁路温度变化与放电特性变化之间存在正反馈的关键是等离子体在壁面的功率沉积随着磁场强度的减小而增大。若这一影响刚好相反,则该交互过程具有负反馈特性,磁路温度便不能引起放电热失稳。所以,在本小节重点对这一影响规律背后的物理机制作进一步的阐述与分析。
首先将壁面沉积的总功率分解为电子功率与离子功率,如图 9所示。可见,电子功率比离子功率大得多;在所有的算例情况下,电子在壁面沉积的功率占了总功率的85%以上。已有文献结合实验与理论研究表明,在某些霍尔推力器上,电子功率沉积占总功率沉积大于80%[26],与本文的模拟结果相近。更进一步可见,壁面功率沉积的变化主要由电子分量引起,离子分量的相对变化较少。
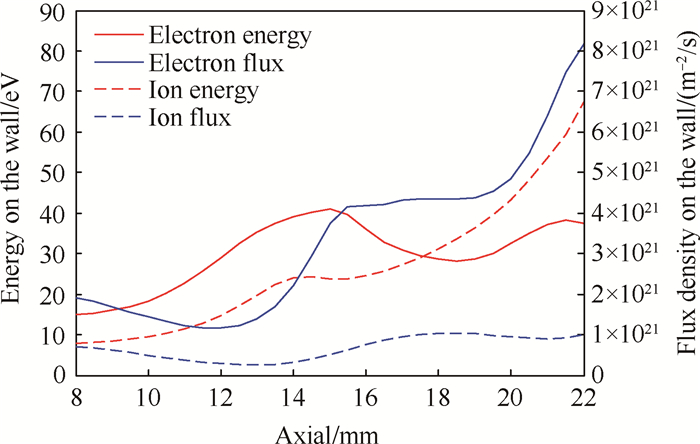
壁面功率沉积是入射到壁面的粒子能量及通量共同作用的结果,通过图 11可以了解到引起电子与离子功率沉积差异较大的原因。可见,在大部分区域,电子入射壁面的能量更大,只有在靠近出口的小范围内由于离子加速效果显现而使得离子入射能量占优;但总体来说,两者相差不大。然而,壁面上的电子入射通量整体上比离子入射通量大得多。正因为如此,在壁面的功率沉积方面电子远大于离子。由图 11可以了解到壁面上电子功率沉积分布的特点:以通道后半段靠近出口区域为主。
|
Fig. 11 Distribution of particle energy and flux density on inner wall |
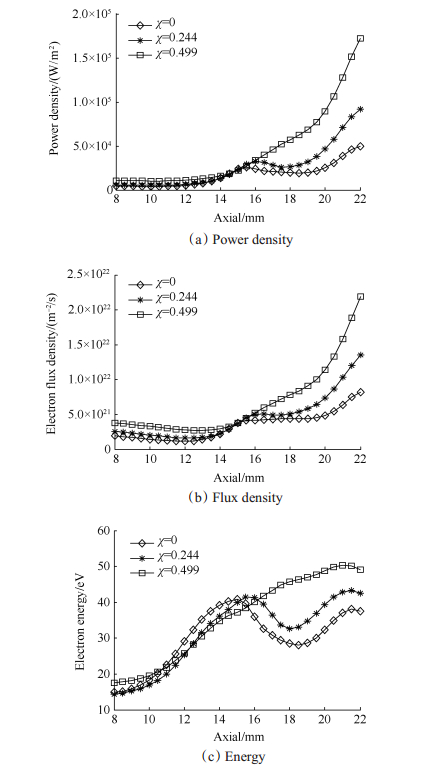
下面着重分析电子功率沉积随着磁场强度减小而增大的原因。图 12(a)是电子在内壁面上沉积的功率密度分布曲线。可见。随着磁场强度的减小,壁面上电子功率沉积分布的变化同样主要发生在通道后半段。而在通道前半段,虽然也有变化,但是相对来说其影响可以忽略不计。进一步通过图 12(b)所示的电子入射到内壁面的通量密度分布与图 12(c)所示的电子入射到内壁面的能量分布的变化来看,在通道后半段,两者随着磁场强度的减小均在单调增大。以上给出的壁面参数分布均是内壁面上的结果;因为外壁面上的变化规律是一样的,所以没有给出。
|
Fig. 12 Distribution of electron parameters deposited on inner wall at different magnetic temperature factor |
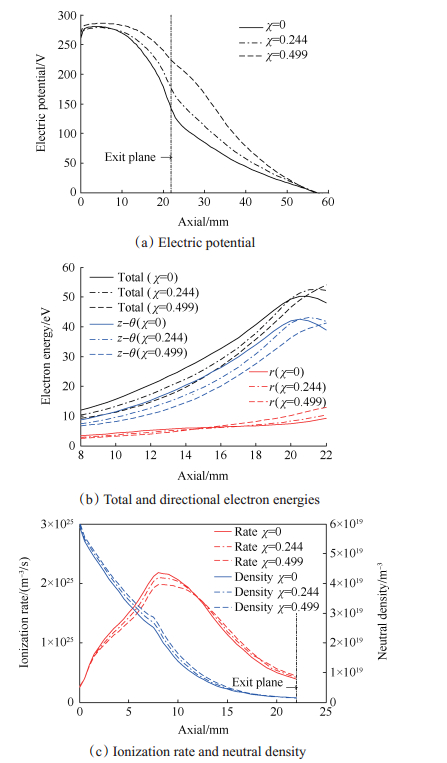
电子入射通量的增加可以通过磁场对电势分布、电子能量各向异性分布以及电离分布的影响来说明。霍尔推力器中的电势分布取决于电子横越磁场形成的电导率分布。在通道内,电导率主要由三部分贡献:一是电子与原子的碰撞,二是电子与壁面的碰撞,三是Bohm碰撞。在通道外,由于原子很少,因此只有Bohm碰撞对电导率有贡献。已有研究表明,在通道内的正梯度磁场中,电导率反比于磁场强度的平方,而在通道外的负梯度磁场中,电导率反比于磁场强度本身。于是,随着磁场强度整体成比例的下降,通道内电导率的相对增大量将大于通道外电导率的相对增大量,这即是说通道内的电阻占放电回路总电阻的比重减小了。因此,如图 13(a)通道中心线上的电势分布曲线所示,随着磁场强度的降低,通道内的电势降减小,通道外的电势降增大。由于阴极发射的电子在从通道外进入通道内时主要被电场加热,所以如图 13(b)通道中心线上的电子能量分布曲线所示,通道出口附近的电子总能量εe随着磁场强度的减小而增大了。此外,从图 13(b)中垂直于径向与平行于径向的电子能量分量ξe, ⊥,ξe, //来看,进入通道的电子能量分布具有各向异性的特征。由于电子在通道外主要依靠Bohm碰撞横越磁场传导到通道内,而Bohm碰撞不会改变电子在垂直于径向与平行于径向方向上的能量分布,所以磁场强度的减小并没有改变通道出口处电子能量分布的各向异性程度;随着磁场强度的减小,ξe, //变大。进一步,由图 7可知,通道后半段的磁力线几乎沿着径向方向,因此电子的各向能量中决定电子与壁面相互作用的主要是径向分量ξe, //。ξe, //越大,入射壁面的电子通量便越大。
|
Fig. 13 Distribution of discharge parameters along channel centerline at different magnetic temperature factor |
当电子从通道出口进一步向通道内运动时,由图 13(b)可见,磁场强度越小,电子总能量的下降速度越快,导致在通道后半段的大部分区域内电子总能量越小。这主要受两个因素作用:其一,电场更小,加热作用减弱;其二,电子在壁面能量损失更大。不过可以发现,电子径向能量分量始终随着磁场的减弱而增大,这就形成了在整个通道后半段电子入射通量更大的条件。关于电子总能量小而径向分量大的原因,可以从电子能量转换的角度来解释。随着磁场的减弱,虽然电子进入通道时的总能量变大,但同时电子向阳极的迁移变快,因此如图 13(c)通道中心线上的电离速率和中性原子密度分布曲线所示,电离分布变宽了,且向通道下游偏移,这样导致的结果是在通道后半段原子密度更大。原子密度的增大使得电子与原子的碰撞频率变大,电子能量在各方向上的转换越频繁且更加趋于各向同性。与此同时,Bohm碰撞频率随着磁场强度的减小而减小,这就使得电子能量趋于各向同性的条件变得更加有利。于是便有了磁场越弱,电子径向能量分量越大的结果。
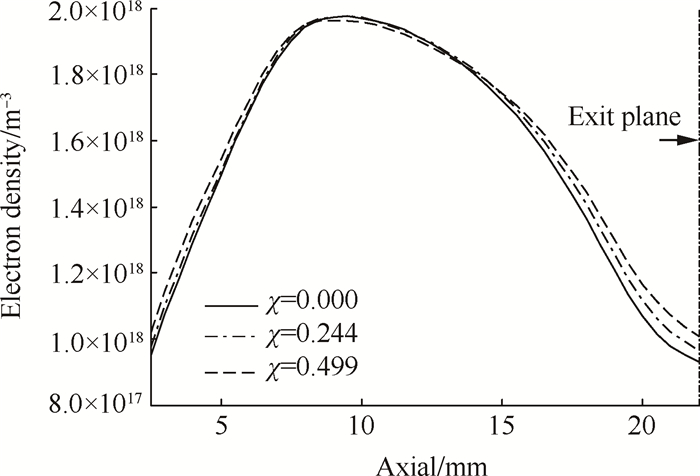
除了由电子径向能量分量导致的电子入射通量的变化之外,另一个重要的因素是通道后半段的等离子体密度分布。由于磁场的减弱使得通道内电势降以及加速电场变小,于是在通道后半段,电离产生的离子速度更小,根据通量守恒定律,离子密度更高。根据等离子体的准电中性特性,电子密度亦更高,与图 14模拟得到的不同磁路温度因子下通道中心线上的电子密度分布变化规律相吻合;于是便会有更多数量的电子入射到壁面。
|
Fig. 14 Distribution of electron density along channel centerline at different magnetic temperature factor |
至于图 12(c)所示电子入射能量随着磁场强度的减小而增大的现象,看似与图 13(b)所示的通道中心线上的电子总能量的变化规律不一致。但这里需要澄清的是,通道中心线上的电子总能量是统计了从通道外进入的高能电子以及高能电子撞击壁面打出的低能二次电子之后的平均结果,而能入射到壁面的电子主要是那些能克服壁面鞘层势垒的高能电子。因此,入射到壁面的那部分电子主要是进入通道的电子,这样便不难理解图 12(c)所示的规律了。
5 结论本文通过对磁路温度影响霍尔推力器放电热稳定性的问题开展实验和Particle-in-Cell数值模拟研究,得到了以下结论:
(1)实验测量磁路温度由室温升高到600℃,工作磁场强度下降了5%。尽管相对变化量较小,但随着磁路温度的升高,通道内磁场强度单调递减。
(2)利用不同强度的磁场等效磁路温度效应,对推力器进行放电模拟分析表明,磁路温度升高导致的磁场强度衰减会使得等离子体在壁面沉积的功率增大,进一步促进磁路的温升。这是一个正反馈过程,因此若推力器的热防护或散热能力不足,将诱发放电热失稳。
(3)等离子体在壁面的功率沉积主要由电子贡献,离子所占的比重很小。更进一步,电子功率沉积随磁路温度的变化主导了壁面总功率沉积的变化,是放电热失稳的主要贡献因素。
(4)电子入射壁面的通量及能量随着磁路温度的升高均增加,共同促进了壁面电子功率沉积的增大。这其中的影响机制是多方面的,其根本是磁场强度的变化改变了通道内外电导率与电势分布的变化,继而对通道内的工质电离与加速过程、电子能量分布等造成了影响。
(5)磁路温度升高到600℃时,工作磁场强度衰减较小,对霍尔推力器性能影响亦较小,因此若不考虑工程应用的实际约束,通过热设计将推力器的磁路温度控制在600℃以内是可以接受的。
| [1] |
Kim V, Popov G, Arkhipov B, et al. Electric Propulsion Activity in Russia[C]. Pasadena, CA: 27th International Electric Propulsion Conference, 2001.
(  0) 0) |
| [2] |
Ahedo E. Plasmas for Space Propulsion[J]. Plasma Physics and Controlled Fusion, 2011, 53(12): 124037. DOI:10.1088/0741-3335/53/12/124037
(  0) 0) |
| [3] |
毛根旺, 韩先伟, 杨涓, 等. 电推进研究的技术状态和发展前景[J]. 推进技术, 2000, 21(5): 1-5. (MAO Gen-wang, HAN Xian-wei, YANG Juan, et al. Research State of Electric Propulsion and Its Development Prospect[J]. Journal of Propulsion Technology, 2000, 21(5): 1-5.)
(  0) 0) |
| [4] |
左坤, 王敏, 李敏, 等. 全电推商业卫星平台研究综述[J]. 火箭推进, 2015, 41(2): 13-20. (  0) 0) |
| [5] |
Grys K, Mathers A, Welander B, et al. Demonstration of 10, 400 Hours of Operation on 4. 5kW Qualification Model Hall Thruster[R]. AIAA 2010-6698. http://arc.aiaa.org/doi/abs/10.2514/6.2010-6698
(  0) 0) |
| [6] |
Kamhawi H, Haag T, Huang W, et al. Performance and Environmental Test Results of the High Voltage Hall Accelerator Engineering Development Unit[R]. AIAA 2012-3854. http://arc.aiaa.org/doi/abs/10.2514/6.2012-3854
(  0) 0) |
| [7] |
严立, 王平阳, 欧阳华. 基于PIC/MCC/DSMC方法霍尔推力器热分析[J]. 推进技术, 2015, 36(6): 953-960. (YAN Li, WANG Ping-yang, OUYANG Hua. Thermal Analysis of Hall Thruster by PIC/MCC/ DSMC Method[J]. Journal of Propulsion Technology, 2015, 36(6): 953-960.)
(  0) 0) |
| [8] |
Mazouffre S, Echegut P, Dudeck M. A Calibrated Infrared Imaging Study on the Steady State Thermal Behaviour of Hall Effect Thrusters[J]. Plasma Sources Science and Technology, 2006, 16(1): 13-22.
(  0) 0) |
| [9] |
Katz I, Mikellides I G, Hofer R R. Channel Wall Plasma Thermal Loads in Hall Thrusters with Magnetic Shielding[R]. AIAA 2011-6082. https://arc.aiaa.org/doi/abs/10.2514/6.2011-6082
(  0) 0) |
| [10] |
Matlock T S, Hargus W A, Larson C W. Thermographic Characterization and Comparison of 200W and 600W Hall Thrusters[R]. AIAA 2007-5241. http://arc.aiaa.org/doi/abs/10.2514/6.2007-5241
(  0) 0) |
| [11] |
Martinez R A, Dao H, Walker M L R. Power Deposition into the Discharge Channel of a Hall Effect Thruster[J]. Journal of Propulsion and Power, 2013, 30(1): 209-220.
(  0) 0) |
| [12] |
Reilly S W, Sekerak M J, Hofer R R. Transient Thermal Analysis of the 12. 5kW HERMeS Hall Thruster[R]. AIAA 2016-5024. http://arc.aiaa.org/doi/abs/10.2514/6.2016-5024
(  0) 0) |
| [13] |
Yan L, Wang P, Ouyang H, et al. Thermal Analysis of the Hall Thruster in Vacuum[J]. Vacuum, 2014, 108: 49-55. DOI:10.1016/j.vacuum.2014.05.003
(  0) 0) |
| [14] |
孙明明, 顾左, 马永斌, 等. LHT-100霍尔推力器热特性模拟分析[J]. 推进技术, 2014, 35(12): 1715-1721. (SUN Ming-ming, GU Zuo, MA Yongbin, et al. Thermal Analysis of a LHT-100 Hall Thruster[J]. Journal of Propulsion Technology, 2014, 35(12): 1715-1721.)
(  0) 0) |
| [15] |
田立成, 高俊, 李兴坤, 等. LHT-100自励磁霍尔推力器热特性测试和热真空实验研究[J]. 推进技术, 2016, 37(4): 793-800. (TIAN Li-cheng, GAO Jun, LI Xing-kun, et al. Experimental Study of Thermal Characteristics and Thermal Vacuum of LHT-100 Self-Excited Hall Thruster[J]. Journal of Propulsion Technology, 2016, 37(4): 793-800.)
(  0) 0) |
| [16] |
Vial V, Godard L, Cornu N, et al. PPS®1350-G Performance Assessment with Permanent Magnets[C]. Wiesbaden: 32nd International Electric Propulsion Conference, 2011.
(  0) 0) |
| [17] |
王二华. 温度对霍尔推力器磁场及放电性能的影响[D]. 哈尔滨: 哈尔滨工业大学, 2014. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D752671
(  0) 0) |
| [18] |
Mitrofanova O A, Gnizdor R Y, Murashko V M, et al. New Generation of SPT-100[C]. Wiesbaden: 32nd International Electric Propulsion Conference, 2011.
(  0) 0) |
| [19] |
Liu H, Wu B, Yu D, et al. Particle-in-Cell Simulation of a Hall Thruster[J]. Journal of Physics D: Applied Physics, 2010, 43(16): 165202. DOI:10.1088/0022-3727/43/16/165202
(  0) 0) |
| [20] |
Ding Y, Peng W, Wei L, et al. Computer Simulations of Hall Thrusters without Wall Losses Designed Using Two Permanent Magnetic Rings[J]. Journal of Physics D: Applied Physics, 2016, 49(46): 465001. DOI:10.1088/0022-3727/49/46/465001
(  0) 0) |
| [21] |
Yu D, Zhang F, Liu H, et al. Effect of Electron Tem perature on Dynamic Characteristics of Two-Dimensional Sheath in Hall Thrusters[J]. Physics of Plasmas, 2008, 15(10): 104501. DOI:10.1063/1.2988766
(  0) 0) |
| [22] |
Szabo J, Warner N, Martinez-Sanchez M, et al. Full Particle-in-Cell Simulation Methodology for Axisymmetric Hall Effect Thrusters[J]. Journal of Propulsion and Power, 2013, 30(1): 197-208.
(  0) 0) |
| [23] |
Szabo J. Fully Kinetic Numerical Modeling of a Plasma Thruster[D]. Cambridge: Massachusetts Institute of Technology, 2001. https://www.researchgate.net/publication/37606639_Fully_kinetic_numerical_modeling_of_a_plasma_thruster
(  0) 0) |
| [24] |
Doss S, Miller K. Dynamic ADI Methods for Elliptic Equations[J]. SIAM Journal on Numerical Analysis, 1979, 16(5): 837-856. DOI:10.1137/0716063
(  0) 0) |
| [25] |
Vahedi V, Surendra M. A Monte Carlo Collision Model for the Particle-in-Cell Method: Applications to Argon and Oxygen Discharges[J]. Computer Physics Communications, 1995, 87(1-2): 179-198. DOI:10.1016/0010-4655(94)00171-W
(  0) 0) |
| [26] |
Grys K, Rayburn C, Haas J. Study of Power Loss Mechanisms in BPT-4000 Hall Thruster[R]. AIAA 2003-5277.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

