2. 中国科学院大学,北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
动力涡轮导叶可调的三轴式船用燃气轮机可以通过调节导叶角度改变动力涡轮的流通能力,从而使燃机具备优异的加减速特性以及低工况特性[1]。然而由于控制量增加,该型燃机的控制系统变得尤为复杂,这就需要对其控制系统展开深入研究。
总体动态仿真模型在燃气轮机控制系统研究中具有重要作用[2]。将模型与控制系统相结合,通过半物理仿真实验,可以为优化控制系统、制定控制策略等提供重要参考,并且避免了直接进行台架试验带来的超温超转等危险工况的发生[3~7]。同时,为了尽可能接近燃气轮机实际动态工况,燃气轮机的仿真模型计算速度应尽可能快,以保证模型具有较高的实时性。常采用的燃气轮机实时建模方法分为几大类:第一类方法为基于燃气轮机工作机理的非线性模型;第二类方法为基于燃机稳态工况的线性化建模法;第三类方法为基于燃气轮机动态工况点,通过系统辨识建立燃气轮机仿真模型。
第一类方法中又包括传统的部件法(Component modeling method,CMM)和容积惯性法[8~11]。然而这类方法无法避免复杂的热力计算,导致模型仿真的实时性受到影响。特别是对于结构复杂的三轴式变几何燃气轮机,由于变量和部件较多,模型的实时性更加难以保证。
第二类方法是在燃机稳态工况的邻域内进行泰勒展开,通过省略非线性项对模型进行简化,增强了模型的实时性[12, 13]。然而,由于燃机模型本身存在强非线性,线性模型在燃机工况变化剧烈或偏离稳态工况较远时,难以准确模拟燃机的工作状况[14]。为此,李永进等进一步保留了非线性余项[15],从而改善了偏离稳态工况较远时模型的仿真精度。
第三类方法需要通过数值计算或实验测量获取大量燃机动态工况点,从而建立输入与输出参数间的对应关系。该类方法避免了复杂的运算过程,具有优异的实时性。动态工况数表法与神经网络法[16]就属于第三类方法。但这类方法用到结构复杂的燃机时,比如本文所研究的带可调导叶的三轴式燃气轮机,由于变量多、自由度大,导致所需动态工况样本点过多。为了减小样本规模,苏明、翁史烈等[17]针对三轴式燃气轮机的工作特性提出了准动态平面法,并取得了较好的结果。然而,该方法是否适用于本文所研究的动力涡轮导叶可调的燃气轮机还有待验证。
目前,在变几何涡轮燃气轮机研究方面,国内外主要的研究重点集中于变几何涡轮部件特性上[18, 19],而对于燃机总体的实时仿真研究较少。本文通过分析动力涡轮导叶可调的三轴式船用燃气轮机的工作特性,合理地选取燃气轮机动态工况样本点以减小样本规模。采用RBF神经网络,结合传统的部件建模方法,建立动力涡轮导叶可调的三轴式变几何燃气轮机实时仿真模型。通过模型计算可知,本文提出的RBF神经网络与部件法的复合建模方法(HMRC)在保证计算精度的前提下,大幅提高了运算速度,确保了模型的实时性。
2 准动态平面法局限性研究图 1为本文研究的动力涡轮导叶可调的三轴式船用燃气轮机结构原理图,前面的高低压转子组成燃气发生器,后面为对外输出功率的动力涡轮。
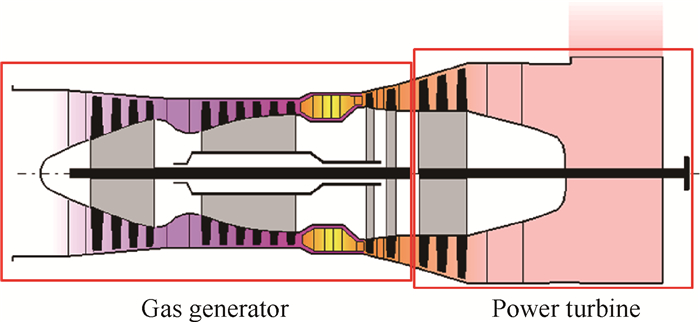
|
Fig. 1 Structure schematic of triaxial gas turbine with variable power turbine guide vane |
准动态平面的提出基于两点假设:(1)在动态过程中,高低压轴转速间的关系基本恒定,可近似取其稳态时的对应关系。(2)动力涡轮转速对仿真结果影响较小,动态计算时可以忽略动力涡轮转速的影响。
实际工况中,特别是针对该型燃机,准动态平面法的假设(1)和假设(2)具有一定局限性,本节将分别进行讨论。首先基于部件法建立燃气轮机仿真模型,从燃机的加减速过程和动力涡轮导叶角度变化两个方面验证高低压转子转速对应关系的不确定性。
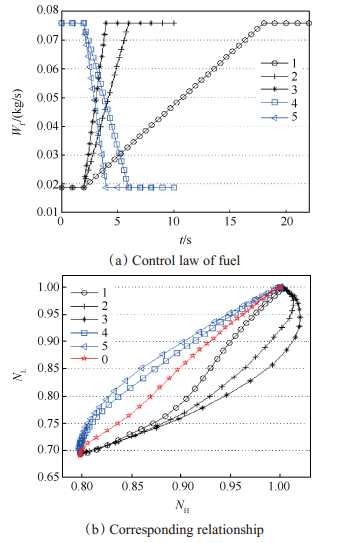
图 2是在动力涡轮导叶角度不变的情况下,不同供油规律高低压转子转速的对应关系,Wf表示燃油流量,NH,NL分别表示高低压轴转速(本文中的转速如无特别说明,均指相对于额定转速的相对转速)。图 2(a)表示了5条供油规律,其中1~3为加油过程,4和5为减油过程。图 2(b)表示燃气轮机动力涡轮导叶角度以及动力涡轮转速不变的情况下,分别按图 2(a)的供油规律变工况运行时,高低压轴转速的对应关系。图 2(b)中,线条0表示稳态工作线。由图可知,加速过程,低压轴转速向低转速方向偏离;减速过程,低压轴转速向高转速方向偏离,且工况变化越剧烈,低压轴转速相对于高压轴滞后效应越明显,高低压轴转速关系偏离稳态工况越远。从图中可以看到不同动态工况下,高压轴转速一定时,低压轴转速浮动范围可达0.15以上。
|
Fig. 2 NH and NL for different fuel supply control laws q |
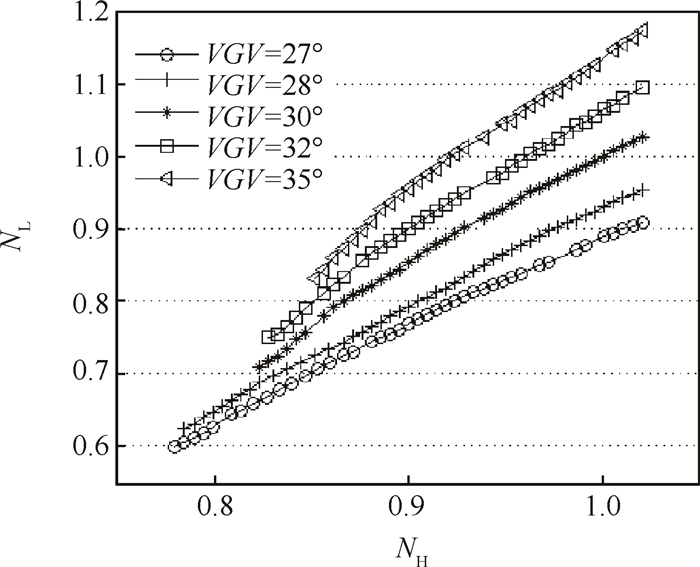
图 3所示为不同动力涡轮进口导叶角度对应的稳态工况下高低压轴间转速的对应关系,VGV表示动力涡轮进口导叶角度,可以看出不同动力涡轮进口导叶角度,高低压轴转速间的关系不同,高压轴转速一定的情况下,低压轴转速浮动范围可达0.2以上。动力涡轮进口导叶角度越大,同一高压轴转速对应的低压轴转速越高。这是因为随着动力涡轮导叶角度增大,动力涡轮流通能力增强,膨胀比降低,导致低压涡轮膨胀比上升,低压轴转速提高。
|
Fig. 3 NH and NL for different angles of power turbine guide vane |
综上,对于动力涡轮导叶可调的三轴式船用燃气轮机,假设(1)难以满足。
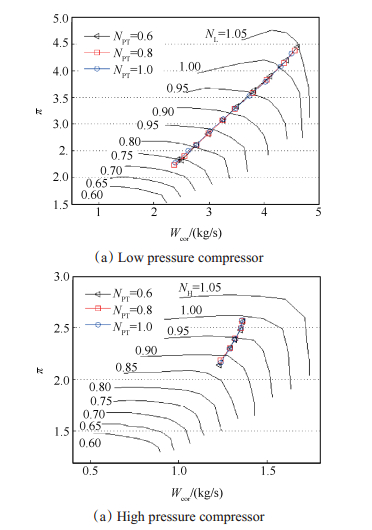
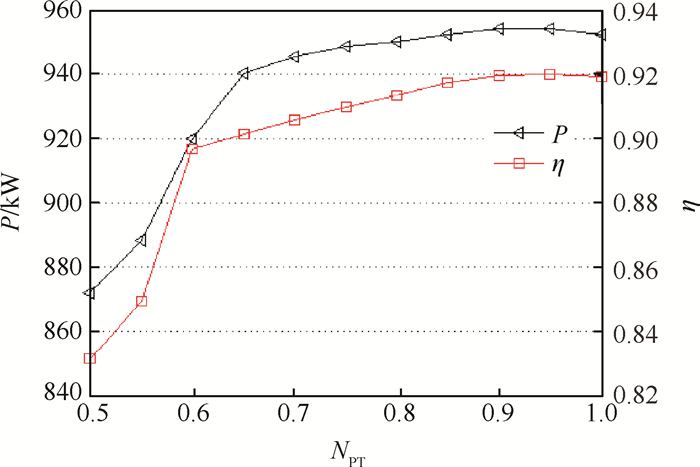
图 4(a),(b)分别显示了不同动力涡轮转速下,低、高压压气机的共同工作线,本文中的π指压气机的压缩比或涡轮的膨胀比,Wcor表示折合流量,NPT为动力涡轮转速。可以看出动力涡轮转速对压气机影响很小。这是由于动力涡轮转速对流通能力影响较小,因此它对燃气发生器的影响也很小。然而,动力涡轮转速对动力涡轮本身的效率和输出功率影响较为显著,动力涡轮相对转速从1降到0.5时,其效率降低了近9%,功率降低了约80kW(见图 5)。P表示输出功率,η表示动力涡轮效率。综上可知动力涡轮转速变化较大时,假设(2)也难以满足。
|
Fig. 4 Operating line for different power turbine rotate speeds |
|
Fig. 5 Computation result of output power and power turbine efficiency |
综上,对于动力涡轮导叶可调的三轴式船用燃气轮机,要使准动态平面法模型达到较高的精度,需要同时满足以下三个条件:(1)燃油流量变化较慢。(2)动力涡轮进口导叶角度不变。(3)动力涡轮转速变化较小。若不满足上述条件,燃气轮机的工作状况会大大偏离准动态平面,此时,即使对准动态平面进行修正也无法解决模型精度降低的问题。因此,对于变几何结构燃气轮机,准动态平面建模方法具有很大的局限性。
3 研究方法燃气轮机处于动态工况时,存在着流量的不平衡,部件内部会有工质的囤积或释放[20]。但流量不平衡对微小型燃机仿真结果影响很小,经过计算验证,本文中的燃气轮机流量不平衡对各参数计算结果的影响均低于千分之一,故流量不平衡的影响因素在燃机仿真中可以忽略,这是本文研究工作的基本假设。
对于动力涡轮导叶可调的三轴式船用燃气轮机,有NH,NL,NPT,低压压气机流量WaLC,高压压气机流量WaHC,燃油流量Wf,高压涡轮流量WaHT,低压涡轮流量WaLT,动力涡轮流量WaPT和VGV共计10个变量。忽略燃气轮机不平衡工况中流量不平衡的影响,动态工况下燃气轮机部件间的相互匹配存在如下流量及压力约束关系
| $ W{a_{{\rm{LC}}}} = W{a_{{\rm{HC}}}} $ | (1) |
| $ W{a_{{\rm{LC}}}} = W{a_{{\rm{HT}}}}-{W_{\rm{f}}} $ |
| $ W{a_{{\rm{LC}}}} = W{a_{{\rm{LT}}}}-{W_{\rm{f}}} $ | (3) |
| $ W{a_{{\rm{LC}}}} = W{a_{{\rm{PT}}}}-{W_{\rm{f}}} $ | (4) |
| $ {\pi _{{\rm{LC}}}} \times {\pi _{{\rm{HC}}}} = {\pi _{{\rm{HT}}}} \times {\pi _{{\rm{LT}}}} \times {\pi _{{\rm{PT}}}} $ | (5) |
式中πLC,πHC,πHT,πLT,πPT分别表示低压压气机、高压压气机压比和高压涡轮、低压涡轮、动力涡轮膨胀比。由方程(1)~(5)中的5个约束关系,燃机的自由变量由10个减为5个,即只需确定Wf,NH,NL,NPT以及VGV五个参数即可唯一确定燃机的某一动态工况。通过计算或实验得到的燃机动态工况样本点,利用系统辨识建立起这五个变量与其他各参数的对应关系,并据此建立实时仿真模型。下文将详细介绍样本点的具体选取方式。
3.1 样本点的选取与计算样本点的具体选取过程如下:Wf可按等差数列在额定燃油流量范围内选取7个值;VGV取27°~35°范围内的5个值;NH在0.75~1转速范围内按等差数列取10个值;NL和NPT的选取可结合前文确定。由上文分析,NPT对燃气发生器的影响较小,故只取1和0.5两个值;由图 3可知不同VGV对应的稳态工况下,NL和NH间的关系式:NL = f (VGV, NH),又由图 2(b)可知,动态工况下NL落在f (VGV, NH) -0.15 ~ f (VGV, NH) + 0.08之间,NL在相对转速0.23的范围内取5个值。
综上,需要计算7×5×10×2×5=3500个动态工况点,该动态工况点利用部件法建立的仿真模型计算得到。对于动力涡轮导叶可调的三轴式船用燃气轮机,传统方法对此五维空间需要计算约5×105个点[21]。可见,此法合理地选取了样本点,大大缩小了样本规模。
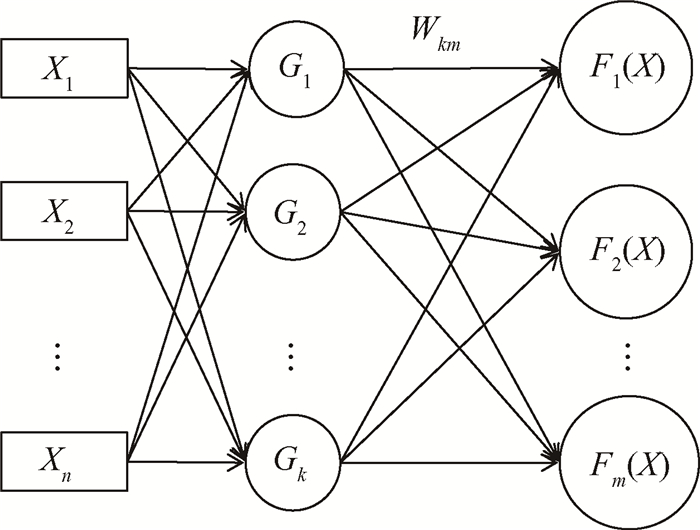
3.2 HMRC实时仿真模型的建立RBF可解决多变量插值时的多维空间曲线拟合问题[22]。RBF神经网络作为一种前馈式神经网络,由于其简单的拓扑结构以及优异的全局逼近能力,在模式识别、信号处理、非线性系统的建模和控制等方面得到了广泛运用[23, 24],具有形式简单、收敛快、泛化能力强等特点。本文采用的RBF神经网络是一种三层前向神经网络(图 6),X1,X2……Xn为输入层,G1,G2……Gk为隐含层,F1,F2,……Fm为其输出层。本文利用基于RBF神经网络的系统辨识法,建立输入层与输出层间的对应关系,从而计算燃气发生器各工作参数。
|
Fig. 6 Topological graph of RBF neural network |
利用3.1中计算的动态工况点训练MATLAB中的RBF神经网络,将训练好的神经网络导入到SIMULINK中。该神经网络输入参数为NH,NL,NPT,VGV,Wf,输出参数为燃机各截面参数和工作参数(含高低压轴加速度)。NPT,VGV以及Wf是输入量,由外部负载和控制系统决定。NH和NL则需要经过计算得到,高低压轴转速随时间的变化由下式计算得到
| $ {N_{{\rm{H}}{t_1}}} = {N_{{\rm{H}}{t_0}}} + \int_{{t_0}}^{{t_1}} {\left( {\frac{{{\rm{d}}{N_{\rm{H}}}}}{{{\rm{d}}t}}} \right)} {\rm{d}}t $ | (6) |
| $ {N_{{\rm{L}}{t_1}}} = {N_{{\rm{L}}{t_0}}} + \int_{{t_0}}^{{t_1}} {\left( {\frac{{{\rm{d}}{N_{\rm{L}}}}}{{{\rm{d}}t}}} \right)} {\rm{d}}t $ | (7) |
将上述方程离散化,得
| $ \begin{array}{l} {N_{{\rm{H}}{t_0}{\rm{ + }}\Delta t}} = {N_{{\rm{H}}{t_0}}} + {\left( {\frac{{{\rm{d}}{N_{\rm{H}}}}}{{{\rm{d}}t}}} \right)_{{t_0}}} \times \Delta t + {\left( {\frac{{{{\rm{d}}^{\rm{2}}}{N_{\rm{H}}}}}{{{\rm{d}}{t^2}}}} \right)_{{t_0}{\rm{ + }}\beta }} \times \frac{{\Delta {t^2}}}{2} \approx \\ \;\;\;\;\;\;\;\;\;\;\;\;\;{N_{{\rm{H}}{t_0}}} + {\left( {\frac{{{\rm{d}}{N_{\rm{H}}}}}{{{\rm{d}}t}}} \right)_{{t_0}}} \times \Delta t \end{array} $ | (8) |
| $ \begin{array}{l} {N_{{\rm{L}}{t_0}{\rm{ + }}\Delta t}} = {N_{{\rm{L}}{t_0}}} + {\left( {\frac{{{\rm{d}}{N_{\rm{L}}}}}{{{\rm{d}}t}}} \right)_{{t_0}}} \times \Delta t + {\left( {\frac{{{{\rm{d}}^{\rm{2}}}{N_{\rm{L}}}}}{{{\rm{d}}{t^2}}}} \right)_{{t_0}{\rm{ + }}\alpha }} \times \frac{{\Delta {t^2}}}{2} \approx \\ \;\;\;\;\;\;\;\;\;\;\;\;\;{N_{{\rm{L}}{t_0}}} + {\left( {\frac{{{\rm{d}}{N_{\rm{L}}}}}{{{\rm{d}}t}}} \right)_{{t_0}}} \times \Delta t \end{array} $ | (9) |
Δt取值越小,转速的计算越准确,相应的模型计算速度越慢。对于本文的研究对象,当Δt小于0.2s后,随着它继续减小,计算结果几乎不变。故本文选取0.2s作为Δt值。
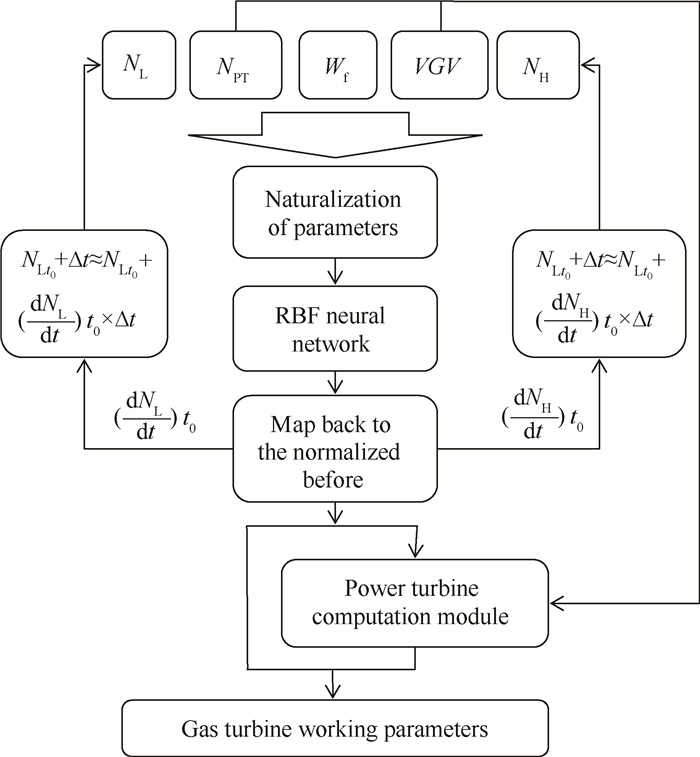
如上文分析,动力涡轮转速对燃气发生器的影响很小,但对燃气轮机输出功率和动力涡轮效率还是有一定影响。为了避免仿真精度降低,本文将实时仿真模型分为两部分,分别采用部件法与RBF神经网络法,其结构示意图如图 7所示。
|
Fig. 7 Structure diagram of real-time simulation model |
燃气发生器模块基于RBF神经网络建立,动力涡轮计算模块基于部件法建立,这种基于RBF神经网络与部件法的复合建模方法(HMRC)建立的实时仿真模型,可兼顾动力涡轮转速变化对其效率和燃气轮机输出功率的影响,从而在减小样本规模的同时,保证实时仿真的精度。
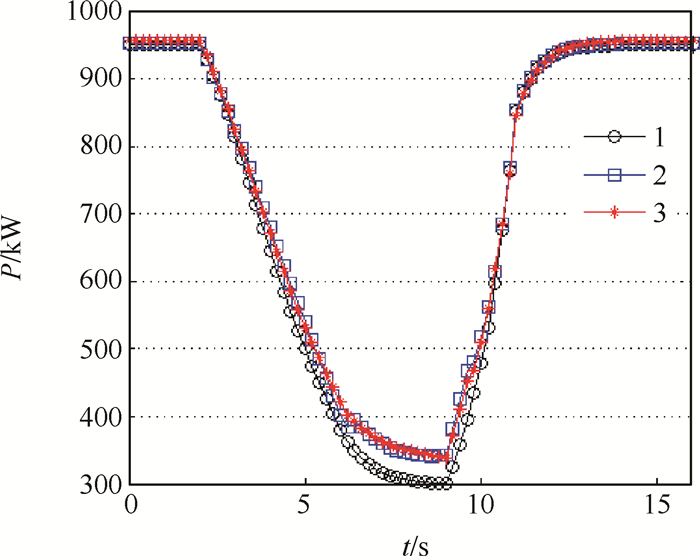
4 结果分析与讨论 4.1 结果验证经测试,对于计算一段燃机36s的动态工况,基于部件法建立的仿真模型耗时17.096604s,采用HMRC建立的实时仿真模型耗时2.58300s。若去掉基于部件法的动力涡轮计算模块,模型耗时2.108697s,实时性会有略微提高,然而模型的准确性却受到较大影响。图 8为三种仿真模型动力涡轮输出功率的计算结果,线条1表示去掉动力涡轮计算模块后神经网络的计算结果,线条2为CMM的计算结果,线条3为HMRC的计算结果,从图中可以看出去掉动力涡轮计算模块仅依靠RBF神经网络后,动力涡轮输出功率的计算出现较大偏差。因此保留动力涡轮计算模块有其必要性。
|
Fig. 8 Comparison of computational results among different simulation models |
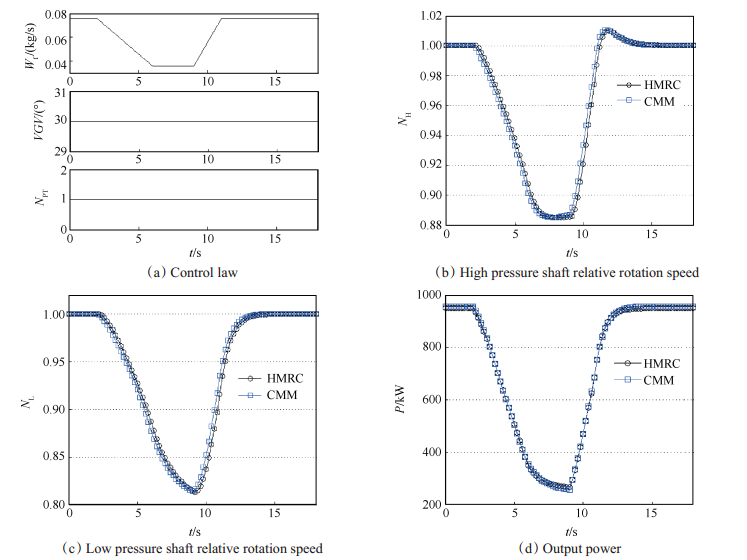
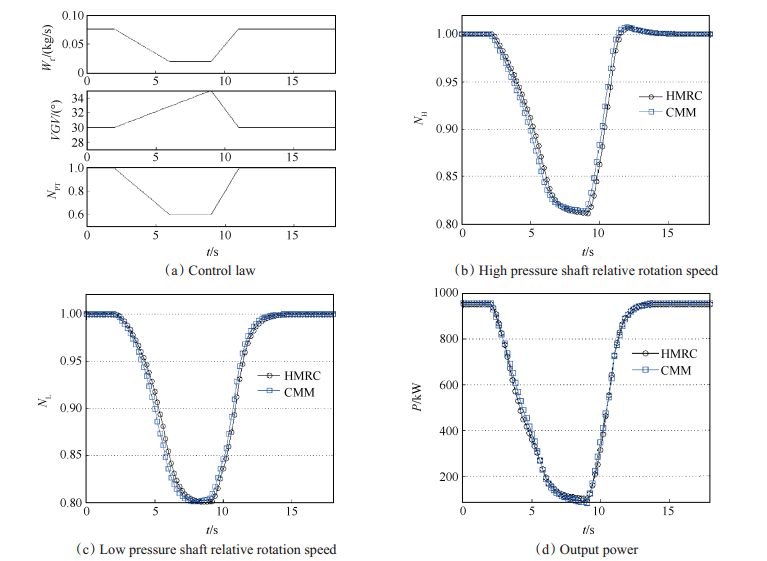
通过给定不同动力涡轮导叶角度变化规律、动力涡轮转速变化规律以及供油规律,可以模拟燃机不同变化规律下燃机的工作状况。图 9为仅Wf变化,VGV,NPT保持不变的单变量仿真,图 10为Wf,VGV,NPT三个变量同时发生变化的多变量仿真。图 9(a)、图 10(a)分别为输入仿真模型的两种变化规律,图 9(b)、图 9(c)、图 9(d)和图 10(b)、图 10(c)、图 10(d)分别展示了两种变化规律下,HMRC与部件法计算结果对比。由图可知,不论是简单的单变量仿真还是复杂的三变量仿真,二者在高低压轴转速和燃机输出功率这三个参数方面吻合度较好。除了这三个参数,HMRC还输出了压气机空气流量、压气机压缩比等共计18个参数,包括燃机各截面参数和燃机各部件性能参数,并可根据需要扩展输出参数。经验证,HMRC与部件法在这些参数上吻合度也很高,本文不再赘述。
|
Fig. 9 Comparison of single variable computational results between HMRC and CMM |
|
Fig. 10 Comparison of multivariable computational results between HMRC and CMM |
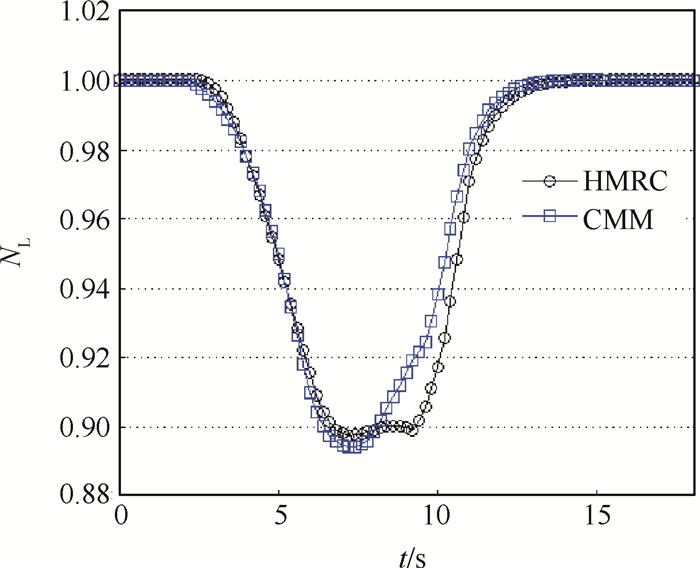
对于多维插值问题,RBF神经网络拥有良好的内插特性,但对于样本点范围外的燃机工况,其外推能力较差。图 11中显示了当动力涡轮导叶角度超出样本27°~35°的取值范围变化到36°时,超出部分偏离了部件法的计算结果。
|
Fig. 11 Comparison of NL computational results between HMRC and CMM |
通过本文研究,得到如下结论:
(1)不平衡工况下,动力涡轮导叶可调的三轴式船用燃气轮机高低压轴转速的对应关系并不固定,在不同供油规律和可调导叶角度变化规律下,高低压转子转速的对应关系在较大范围内变动,准动态平面法应用于动力涡轮导叶可调的三轴式船用燃气轮机时具有局限性。
(2)NPT对三轴式燃气轮机燃气发生器的工况影响很小,但对动力涡轮效率和燃气轮机输出功率有较大影响。
(3)对于动力涡轮导叶可调的三轴式船用燃气轮机实时仿真模型,本文提出的HMRC可将原来的5维问题简化为准4维问题,在保证仿真精度和实时性的同时,减小样本规模。
(4)由于RBF神经网络的外推能力较弱,需要注意确定样本点的取值范围,防止当燃机工况超出样本点范围时,模型计算精度难以保证。
在后期的研究工作中,将通过半物理仿真实验以及燃机的台架实验数据进一步验证HMRC的可靠性。
| [1] |
冯永明, 黄全军, 刘顺隆, 等. 舰船燃气轮机变几何动力涡轮通流特性的数值研究[J]. 燃气轮机技术, 2005, 18(2): 37-43. (  0) 0) |
| [2] |
Smith D L, Stammetti V A. Sequential Linearization as an Approach to Real Time Marine Gas Turbine Simulation[R]. ASME GT 1989-203. http://www.researchgate.net/publication/237900234_Sequential_Linearization_as_an_Approach_to_Real_Time_Marine_Gas_Turbine_Simulation
(  0) 0) |
| [3] |
Qusai Z A, Munzer S Y. Modeling and Simulation of a Gas Turbine Engine for Power Generation[J]. Journal of Engineering for Gas Turbines and Power, 2006, 128(2): 302-311. DOI:10.1115/1.2061287
(  0) 0) |
| [4] |
李淑英, 李铁磊, 王志涛. 船舶燃气轮机发电机组实时仿真新方案[J]. 哈尔滨工程大学学报, 2014, 35(1): 69-73. (  0) 0) |
| [5] |
Alcaide I X, Hernandez I, Garduno R. Real-Time Simulation of a Gas Turbine Driven Power Plant for Control System Design[R]. IFAC, 9555-9560, 2011. https://www.researchgate.net/publication/268007692_Real-Time_Simulation_of_a_Gas_Turbine_Driven_Power_Plant_for_Control_System_Design
(  0) 0) |
| [6] |
Jaw L C, Mat C, Mattingly J D. Aircraft Engine Controls, Design, System Analysis, and Health Monitoring[M]. Virginia: American Institute of Aeronautics and Astronautics, 2009.
(  0) 0) |
| [7] |
Lietzau K, Kreiner A. Model Based Control Concepts for Jet Engines[R]. ASME GT 2001-0016. https://www.researchgate.net/publication/267483256_Model_Based_Control_Concepts_for_Jet_Engines
(  0) 0) |
| [8] |
左志涛. 燃气轮机整机性能仿真研究[D]. 北京: 中国科学院工程热物理研究所, 2012.
(  0) 0) |
| [9] |
Chacartegui R, Sánchez D, Muñoz A, et al. Real Time Simulation of Medium Size Gas Turbines[J]. Energy Conversion and Management, 2011, 52(1): 713-724. DOI:10.1016/j.enconman.2010.07.050
(  0) 0) |
| [10] |
Camporeale S M, Fortunato B, Mastrovito M. A Modular Code for Real Time Dynamic Simulation of Gas Turbines in Simulink[J]. Journal of Engineering for Gas Turbines and Power, 2006, 128(7): 506-517.
(  0) 0) |
| [11] |
苏明, 陈德来, 张园蔚, 等. 一种燃气轮机模块化非线性仿真模型[J]. 热能动力工程, 1998, 13(6): 435-437. (  0) 0) |
| [12] |
Chung G Y, Prasad J V R, Dhingra M, et al. Real Time Analytical Linearization of Turbofan Engine Model[J]. Journal of Engineering for Gas Turbines and Power, 2014, 136(1): 1250-1262.
(  0) 0) |
| [13] |
宋志平, 韩崇昭, 魏瑞轩. 基于发动机非线性响应的辨识线性模型方法[J]. 推进技术, 2005, 26(2): 155-157. (SONG Zhi-ping, HAN Chong-zhao, WEI Rui-xuan. Method to Identify the Multimode Linear Model of Aeroengine Based on Nonlinear Response[J]. Journal of Propulsion Technology, 2005, 26(2): 155-157.)
(  0) 0) |
| [14] |
吴海燕. 分轴燃气轮机的建模和仿真研究[D]. 上海: 上海交通大学, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10248-1013021696.htm
(  0) 0) |
| [15] |
李永进, 张海波, 张天宏. 一种考虑非线性余项的机载发动机自适应模型建立及其在寻优控制中的应用[J]. 推进技术, 2016, 37(1): 172-180. (LI Yongjin, ZHANG Hai-bo, ZHANG Tian-hong. Establishment and Application in Performance Seeking Control of an On-Board Adaptive Aero-Engine Model Considering Nonlinear Remainders[J]. Journal of Propulsion Technology, 2016, 37(1): 172-180.)
(  0) 0) |
| [16] |
曾进, 任庆生, 翁史烈, 等. 基于神经网络的燃气轮机动态过程仿真[J]. 热能动力工程, 2000, 15(4): 423-425. (  0) 0) |
| [17] |
苏明, 翁史烈, 张伯年. 船用三轴燃气轮机动态过程实时仿真的数学模型[J]. 上海交通大学学报, 1990, 24(3): 1-7. (  0) 0) |
| [18] |
冯永明, 刘顺隆. 舰船燃气轮机变几何动力涡轮三维粘性流场的数值分析[J]. 哈尔滨工程大学学报, 2005, 26(5): 580-585. (  0) 0) |
| [19] |
李天禄, 乔渭阳. 变几何涡轮流动机制及气动性能数值模拟研究[J]. 科学技术与工程, 2012, 12(35): 9602-9607. DOI:10.3969/j.issn.1671-1815.2012.35.031 (  0) 0) |
| [20] |
Fawke A J, Saravanamuttoo H I H. Digital Computer Simulation of Dynamic Response of Twin-Spool Turbofan with Mixed Exhausts[J]. Aeronautical Journal, 1973, 77: 471-478.
(  0) 0) |
| [21] |
曾进, 任庆生, 翁史烈, 等. 基于神经网络的燃气轮机动态过程仿真[J]. 热能动力工程, 2000, 15(4): 423-425. (  0) 0) |
| [22] |
穆云峰. RBF神经网络学习算法在模式分类中的应用研究[D]. 大连: 大连理工大学, 2006. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1030238
(  0) 0) |
| [23] |
乔俊飞, 韩红桂. RBF神经网络的结构动态优化设计[J]. 自动化学报, 2010, 36(6): 865-872. (  0) 0) |
| [24] |
王志涛, 李淑英, 谭智勇. 基于BP和RBF神经网络压气机特性曲线拟合方法的研究[J]. 汽轮机技术, 2009, 51(2): 94-96. (  0) 0) |
 2018, Vol. 39
2018, Vol. 39

