2. 火箭军工程大学 青州士官学院,山东 青州 262500;
3. 西安航天动力研究所,陕西 西安 710100
2. Non-Commissioned Officer Institute, Rocket Force University of Engineering, Qingzhou 262500, China;
3. Xi'an Aerospace Propulsion Institute, Xi'an 710100, China
凝胶火箭推进剂(Gelled Rocket Propellant,GRP)兼有液体推进剂和固体推进剂的优势,能够有效提高火箭发动机的操控性、安全性、可靠性等指标,在未来快速打击导弹武器系统中具有广阔的应用前景[1, 2]。实用化的凝胶推进剂中大都含有铝、碳、硼等固体含能颗粒成分,而固体含能颗粒的添加可以有效提高凝胶推进剂的密度及热力学性能,对凝胶推进剂的流变和雾化特性也存在着重要的影响[3]。雾化过程中的液膜、液丝及液滴速度速度分布、液膜厚度等参数是燃烧室中液丝/液滴速度及尺寸的直接表征、是雾化理论分析中的重要参数、是雾化数值模拟中的重要参考指标,对于判断雾化效果、揭示雾化机理具有重要作用。在目前凝胶推进剂雾化理论分析中,使用的液膜速度、厚度等参数大多为理论值或假设值,液膜破碎特性的理论分析结果与实验值误差较大。
实验是凝胶推进剂雾化研究的主要手段,目前国内外公开报道的含固体颗粒的凝胶推进剂雾化研究十分有限。2003年,Jayaprakash等[4]使用了含铝颗粒的煤油凝胶进行实验,但是,从其研究中难以得出铝颗粒的添加对雾化的影响。2007年,Kampen等[5]对添加不同浓度的铝颗粒的凝胶Jet A-1燃料的流变、雾化及燃烧特性进行了详细研究,结果表明,所有添加铝颗粒的凝胶均表现出明显的屈服应力,铝浓度的增大造成剪切粘度的增大,会使液膜的宽度增大、破碎长度增长;当改变广义雷诺数及铝颗粒浓度时,会出现射线型、液丝型、完全发展型等三种不同的雾化模式。2011年,Baek等[6]对比研究了水、不含/含SUS304颗粒的聚羧乙烯凝胶的雾化特性,研究发现,随着撞击速度的提高,水及不含颗粒的聚羧乙烯凝胶形成的液膜均会增大,但含SUS304颗粒的凝胶液膜并不随着速度变化而变化。2012年,张蒙正等[7]使用N2O4凝胶和添加10%碳颗粒的UDMH凝胶进行了燃烧效率实验,研究表明,添加碳粉后凝胶体系的粘度略有增大,造成雾化效果变差,燃烧效率下降。上述较为有限的研究文献中,都是以定性分析雾化图像为基础,很难系统、定量地分析固体颗粒的添加对凝胶推进剂流变及雾化等的影响。而目前对于雾化场速度的研究也是以实验测量液滴速度为主。Rodrigues等[8]应用相多普勒测速仪实验测量了两种水基凝胶推进剂模拟液雾化后的液滴尺寸和液滴速度,研究表明,撞击角度和自由射流长径比对液滴尺寸影响不大,而增大喷嘴内长径比可以产生更大的液滴直径。陈杰等[9]应用时间分辨粒子图像测速系统(TR-PIV),研究了不同撞击角度和射流压差对凝胶推进剂雾化速度的影响,研究发现,距撞击点越远,雾化场速度越小且分布越均匀,增大撞击角和射流压差都可以提高雾化质量。
与实验相比,数值模拟可以获得实验无法测量的剪切速率压力等物理量的变化规律,将仿真结果与实验现象理论预测相结合,有助于进一步的揭示雾化机理。但是基于其复杂性,长期以来,雾化问题的数值模拟研究进展缓慢。2010年,Arienti等[10]采用AMR(Adaptive Mesh Refinement)技术和CLSVOF(Coupled Level Set & VOF)方法,同时结合Lagrange粒子追踪技术,分别数值模拟了水射流在低速和高速状态下的撞击雾化过程,得到了液滴尺寸和粒径分布,并与实验结果进行了对比,证明了该方法的有效性。2011年,Ma D J等[11]基于VOF(Volume of Fluid)方法,对牛顿及非牛顿流体双股射流撞击的一次雾化进行了数值模拟,其中非牛顿流体使用了Herschel-Bulkley本构模型,得到了非牛顿流体的两种雾化模式,同时,其研究结果表明,粘性力和表面张力是导致液膜破碎的主要因素。强洪夫等[12]探索性地应用SPH(Smoothed Particle Hydrodynamics)方法进行了非牛顿射流撞击雾化问题的数值模拟,雾化实践表明,SPH方法可以有效仿真射流撞击液膜形成液膜破碎的典型过程,仿真结果与实验现象基本一致。
本文以双股射流凝胶推进剂模拟液撞击雾化实验为基础,通过尺度不变特征变换(Scale Invariant Feature Transform,SIFT)算法提取雾化场图像的关键点,利用几何关系并结合雾化问题的特点对前后两幅雾化场图像的关键点进行精确匹配,计算出关键点位移和速度;基于关键点的速度计算分析了不同工况下的雾化场速度分布及平均速度随撞击角度、射流速度等因素的变化规律;以雾化场速度分析为基础,提出了一种新的液膜厚度估算方法,讨论了液膜厚度随着撞击角度、射流速度的分布;通过理论分析、与实验结果进行对比验证等手段,验证了本文提出的速度计算方法、液膜厚度估计方法正确性和有效性。
2 雾化实验为了深入研究射流速度,撞击角度以及碳颗粒的质量分数、平均粒径等因素对凝胶推进剂雾化效果的影响,本文设计了三种不同的凝胶推进剂模拟液在不同射流速度(vjet≈10,20,30,40m/s)、不同撞击角度(2θ=40°,60°,80°,90°)条件下的雾化实验。实验采用双股射流撞击式雾化,撞击式喷嘴的喷口直径d=1mm,喷口长径比L/d=6。
本文制备了三种含碳颗粒凝胶推进剂模拟液SC1~SC3,三种模拟液的基质均为去离子水、胶凝剂含量均为1%,主要区别在于碳颗粒的含量及平均粒径的不同,具体组分见表 1。经过测量,SC1~SC3模拟液的密度均略高于水,密度值分别为1010.3kg/m3,1036.3kg/m3,1064.0kg/m3;表面张力系数与水基本一致,σ=0.073N/m。
|
|
Table 1 Composition of three kinds of carbon-loaded gelled propellant simulants |
图 1为实验得到的典型雾化图像,模拟液为SC1,撞击角均为60°,射流速度依次为vjet≈10,20,50m/s。从图中可以看出,随着雾化条件的不同,根据雾化场内液膜的基本形状可以将雾化现象分为三种基本类型:边缘闭合型(图 1(a))、边缘开放型(图 1(b))、液丝-液滴型(图 1(c))。

|
Fig. 1 Different modes of atomization field |
如图 1(a)所示,两股射流撞击后形成表面积较小的、具有清晰边缘的近似椭圆形液膜,液膜下端边缘流体收缩汇成一股,该模式被称为边缘闭合型雾化模式。边缘闭合型雾化模式没有液丝或液滴的形成,射流撞击的最终结果是形成一股竖直向下流动,两股射流的混合效果及射流撞击前后的表面积增量都非常有限,因此,边缘闭合型雾化模式的雾化效果较差。
当射流撞击后形成的液膜面积明显增大,液膜表面出现一定的波动(扰动波),液膜下端敞开并有少量液丝生成,形成图 1(b)所示的边缘敞开型雾化模式。
随着液膜表面的扰动波进一步加强,液膜下缘破碎形成液丝的距离减小,液膜两侧边缘逐渐模糊,雾化角略有增大,液丝在运动过程中会进一步变形、断裂、破碎形成液滴,这种被称为液丝-液滴型(图 1(c))。
3 基于SIFT关键点匹配的雾化场速度计算方法SIFT算法是加拿大学者Lowe提出的一种特性匹配算法[13, 14],该算法基于多尺度空间理论,具有良好的尺度、旋转不变性,对光照、视角变化、噪声和仿射变换等具有较强的鲁棒性,且提取关键点稳定、数量丰富,被广泛应用于图像配准、影像缝合、影像追踪和动作对比等领域[15]。
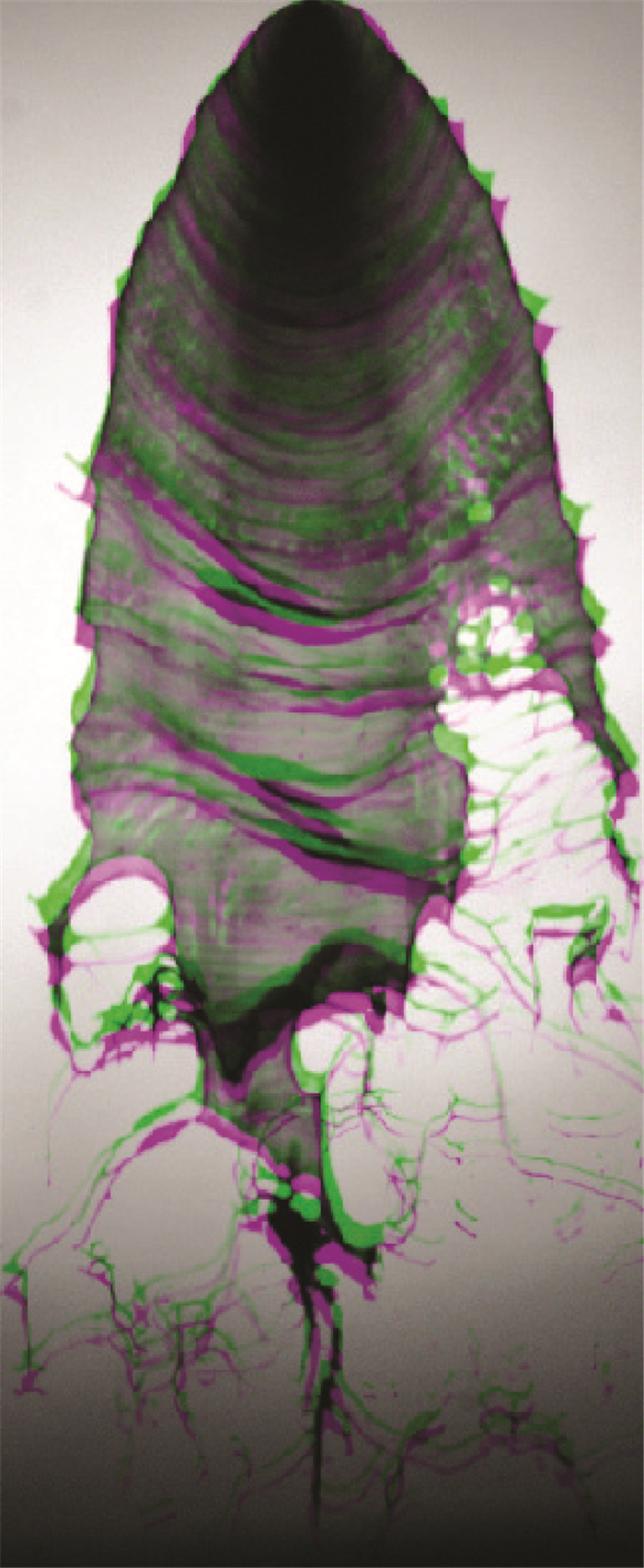
图 2为射流速度vjet=20.05m/s,撞击角2θ=60°时相邻时刻的雾化场图像进行叠加融合显示的结果,可以看出,t时刻与t+Δt时刻图像在液膜内部的扰动波、液膜外缘、液丝等部位具有非常明显的对应关系,t+Δt时刻雾化场可以看作是t时刻雾化场向下运动并发生一定变形后的结果。因此,本文采用尺度不变特征变换(SIFT)算法,提取t时刻与t+Δt时刻雾化场图像中具有典型几何或光学等特征的点并建立这些点的对应关系,进而求得这些点处的速度场。
|
Fig. 2 Overlapping display of atomization images at adjacent time |
(1)尺度空间极值点检测
SIFT算法利用高斯差分和图像金字塔构建尺度空间、检测尺度空间极值。对于图像I(x, y),其尺度空间函数L(x, y, σ)定义为尺度可变高斯核函数G(x, y, σ)与图像I(x, y)的卷积,即
| $ L\left( x, y, \sigma \right)=G\left( x, y, \sigma \right)\cdot I\left( x, y \right) $ | (1) |
| $ G\left( {x, y, \sigma } \right)=\frac{1}{{2\pi {\sigma ^2}}}{{\rm{e}}^{-\left( {{x^2} + {y^2}} \right)/2{\sigma ^2}}} $ | (2) |
式中·表示卷积运算,σ为尺度空间因子,σ的值决定着图像的被光滑程度。
DoG(Difference-of-Gaussian)金字塔定义为相邻尺度空间函数的差值,即
| $ D\left( {x, y, \sigma } \right)=L\left( {x, y, k\sigma } \right)-L\left( {x, y, \sigma } \right) $ | (3) |
将DoG金字塔中的每个像素点与同层的8个像素点及上下两层的各9个像素点进行比较,以找到尺度空间的局部极值点。所有这些局部极值点构成了SIFT算法的候选关键点集合。本文计算中,空间尺度因子σ取初值0.8,尺度比例k=1.256。
获取局部极值点后,还需要进行剔除低对比度的点及不稳定的边缘响应点,以提高关键点匹配稳定性及抗噪声能力。
(2)关键点方向确定
关键点的梯度模值m(x, y)及方向θ(x, y)由下式得到
| $ m\left( {x, y} \right)=\sqrt {{{\left( {L\left( {x + 1, y} \right)-L\left( {x-1, y} \right)} \right)}^2} + {{\left( {L\left( {x, y + 1} \right)-L\left( {x, y - 1} \right)} \right)}^2}} $ | (4) |
| $ \theta \left( {x, y} \right)={\tan ^{-1}}\left( {\left( {L\left( {x, y + 1} \right)-L\left( {x, y-1} \right)} \right)/\left( {L\left( {x + 1, y} \right) - L\left( {x - 1, y} \right)} \right)} \right) $ | (5) |
式中L表示关键点所在的尺度空间。
经上述处理,每一个SIFT关键点都具有了位置、尺度及方向三个信息。由此可以确定一个SIFT特征区域。
(3)关键点特征描述符生成
通过以下步骤为检测到的SIFT关键点建立统一的特征向量描述符:
① 将图像坐标轴旋转为关键点主方向,以保证旋转不变性。
② 以关键点为中心取16×16的窗口,将其均匀分为4×4的子区域,对每一子区域计算8个方向的梯度方向直方图,这样每个关键点具有了4×4×8=128维向量。
③ 将SIFT关键点描述符进行归一化,使SIFT关键点描述符同时具备尺度、旋转及亮度不变性。
3.2 雾化场关键点匹配传统SIFT算法一般利用欧氏距离作为相似性度量,匹配两幅图像的SIFT关键点。计算参考图像中某一关键点与待配准图像的所有关键点之间的欧氏距离,找出最小距离dmin及次最小距离dscn,计算其比值rd=dmin/dscn。当rd<rthresh时,认为两关键点匹配。Lowe[14]推荐的阈值rthresh=0.8,降低这个阈值,SIFT匹配点数目会减小,但更加稳定[15]。因此,在本文计算中,取rthresh=0.6。对图 2所示的图像进行SIFT关键点匹配,共得到了751对匹配的SIFT关键点,为进一步修正匹配误差,本文根据凝胶推进剂雾化场的特点(雾化场内绝大多数点以撞击点为中心向外向下运动,同时雾化场液膜运动速度小于射流速度),对SIFT算法匹配后的关键点进行了进一步筛选。经过筛选,得到了690对匹配的关键点,有效修正了单独应用欧氏距离作为匹配准则时出现的关键点错配问题,匹配结果更加准确。
3.3 雾化场速度计算t时刻雾化图像的关键点Pi(xPi, yPi)处的速度可通过下式计算
| $ {\mathit{\boldsymbol{v}}_{{p_i}}}{\rm{=}}\frac{{\frac{1}{{{\gamma _{ir}}}}\left( {{\mathit{\boldsymbol{r}}_{{Q_i}}}-{\mathit{\boldsymbol{r}}_{{p_i}}}} \right)}}{{\Delta t}} $ | (6) |
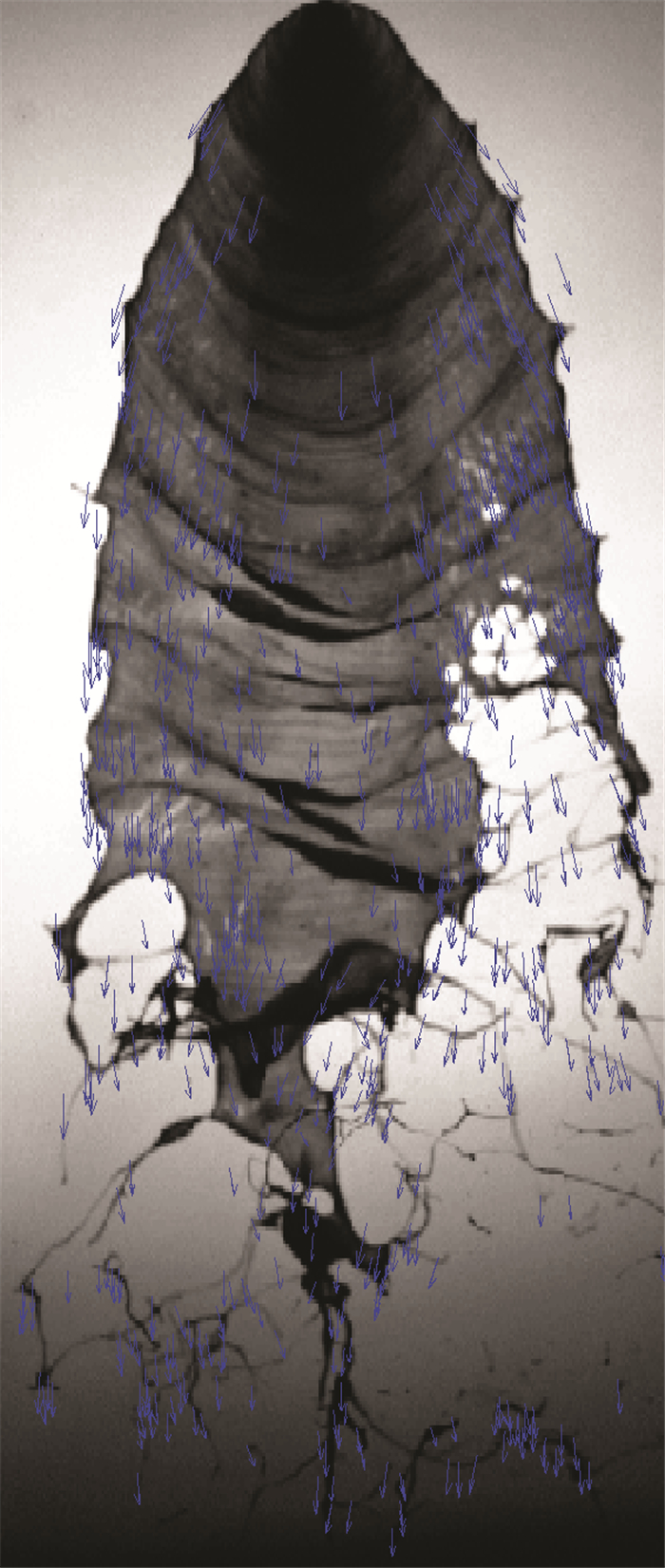
式中vPi=(uPi, vPi)T为Pi(xPi, yPi)的速度矢量,rPi=(xPi, yPi)T,rQi=(xQi, yQi)T,γir=3920pixel/m为图像距离(像素)与实际尺寸(米)的比值,Δt=0.2μs为雾化图像的拍摄时间间隔。由此计算出的雾化场SIFT关键点速度矢量如图 3所示。可以看出,雾化场SIFT关键点的速度以撞击点为中心呈辐射状向外散开,速度分布与雾化场的形状非常相符。
|
Fig. 3 Vector graph of velocity of the key points in atomization field |
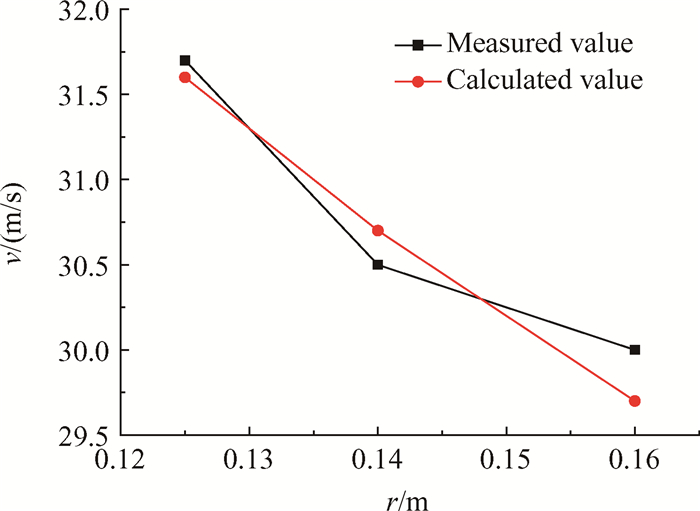
为了对速度计算精度进行考察,本文利用PDPA(相位多普勒粒子分析仪)光学系统对雾化效果相对较好、雾化场下游存在一定液滴的工况下不同截面的液滴速度进行了测量(撞击角60°,射流速度vjet≈50m/s,对于其它工况,雾化场主要由液丝及少量大尺寸液滴构成,液丝速度难以测量)。测量结果与本文方法计算出的速度对比如图 4所示。可以看出,液滴速度的计算值与实验测量值非常一致,二者的最大偏差小于0.3m/s。这表明,本文提出的雾化场速度计算方法,计算精度较高,计算结果可靠。
|
Fig. 4 Comparison of measured and calculated values of droplets velocity |
为进一步提高雾化场速度计算的准确度,本文采取了以下处理方法:设t -Δt,t,t + Δt时刻的雾化图像分别为I1,I2,I3,分别计算I1 -I2,I2 -I3之间匹配的SIFT关键点,而后,筛选出I2上与I1,I3都匹配的关键点,计算出其速度。
4.1 雾化场速度分布本文研究了不同工况下以撞击点为圆心半径为r的圆弧上的速度分布。
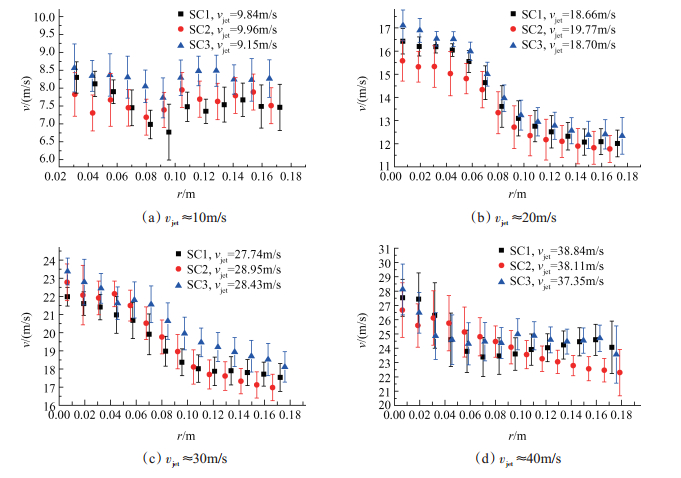
图 5为2θ=60°,vjet≈10,20,30,40m/s时,SC1~ SC3模拟液的雾化场速度随着与撞击点距离r的分布。图 6为vjet≈20m/s,2θ=40°,60°,80°,90°时,SC1~ SC3模拟液的雾化场速度随着距离r的分布。图中表示的是速度的统计学分布,不同的图标所代表点处的数值表示与撞击点距离相同的所有速度的均值,线段的半长度则代表标准差。从图 5,图 6可以看出,雾化场速度随着与撞击点距离r的分布规律与雾化场中流体以撞击点为中心向周围辐射展开的物理现象是一致的。
|
Fig. 5 Distribution of the atomization field velocity with the distance from impact point(2θ=60°) |
|
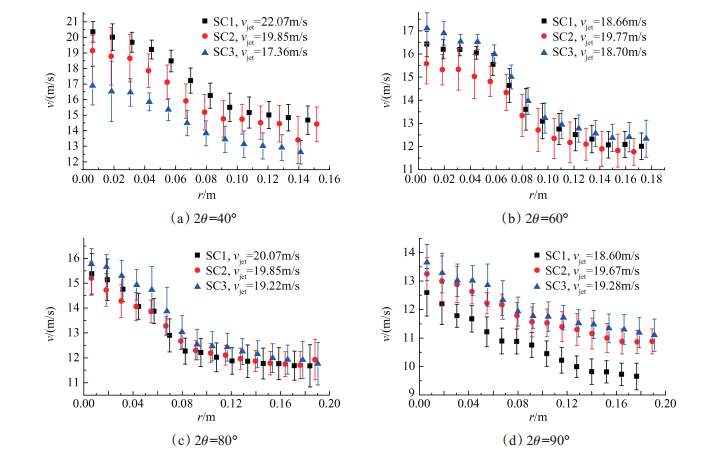
Fig. 6 Distribution of the atomization field velocity with the distance from impact point(vjet≈20m/s) |
(1)由于射流撞击雾化过程中的粘性耗散等因素,对于图 5,图 6所示的所有工况,雾化场速度均明显小于射流速度;图 6(a)~(d)的整体对比看出,射流速度基本相同时,雾化场速度随着撞击角度的增大而减小,这主要是由于射流的有效撞击速度随撞击角度的增大而增大,雾化过程中的能量耗散增大所致。
(2)通过对比雾化模式与速度分布可以发现,图 5(a)所示工况(边缘封闭型雾化模式)与其它工况(边缘敞开型及液丝-液滴型雾化模式)在速度分布上具有明显差别,其雾化场速度随着与撞击点距离的增大呈现出先下降后上升最后基本稳定的趋势,这与边缘封闭雾化模式中出现的射流撞击展开形成小面积的液膜-液膜下缘收缩-汇成一股下流的现象是一致的;而对于图 5(b)~(d),图 6(a)~(d)所示的工况,由于雾化过程中液膜的展开、破碎及液丝的变形、断裂等过程不断消耗流体的动能,因此,雾化场速度整体上随着与撞击点距离的增大而减小。
(3)由图 5(a)~(d),图 6(b)~(d)看出,在射流速度、撞击角度相同时,SC3模拟液的雾化场速度普遍略高于SC1,SC2模拟液的雾化场速度,这是由于与SC1,SC2模拟液相比,SC3模拟液的碳颗粒粒径更大,射流撞击时,碳颗粒间相互作用更为明显、胶凝剂对碳颗粒的约束作用相对较小、粘性耗散相对较小,因此,射流撞击后剩余动能较大、速度较高。
4.2 雾化场平均速度凝胶推进剂的射流撞击雾化是一个高度紊乱、复杂的过程,为进一步揭示不同工况下雾化场速度的变化规律,本文对上述雾化图像的速度进行加权平均,获得雾化场的平均速度并进行分析讨论。
图 7、图 8分别为SC1~SC3模拟液的雾化场平均速度随射流速度、撞击角度的变化规律。
|
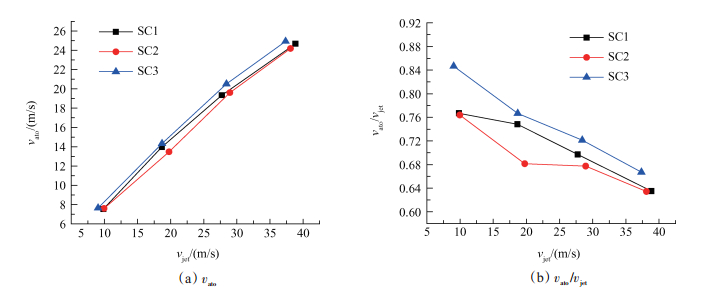
Fig. 7 Variation of average velocity of atomization field with jet velocity(2θ=60°) |
|
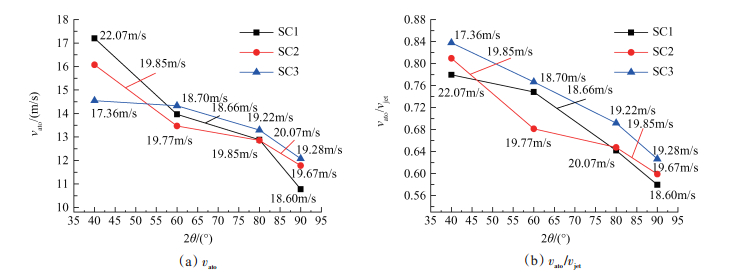
Fig. 8 Variation of average velocity of atomization field with impact angle |
由图 7(a)可以看出,2θ=60°时,雾化场平均速度随射流速度的增大而近似呈线性增大;图 7(b)表明,雾化场平均速度与射流速度的比值并非定值,而是随着射流速度的增大而减小,vato/vjet的变化范围为0.6~0.9,与Heislbetz等[16]提出的
由图 8看出,在射流速度相同时,同种模拟液的vato及vato/vjet均随着撞击角度的增大而减小。
凝胶推进剂的射流撞击雾化是射流动能通过变形、耗散等转换为势能的过程,能量转换越充分,雾化效果越好。雾化场平均速度是转换后剩余动能的表征,因此,雾化场平均速度与射流速度的比值vato/vjet可作为能量转换效率的度量,用于表征雾化效果。对同一种凝胶推进剂模拟液而言,vato/vjet越小,说明能量转换效率越高,雾化效果越好。由图 7(b)、图 8(b),同一种凝胶推进剂模拟液的vato/vjet随着射流速度、撞击角度的增大而减小,说明凝胶推进剂模拟液的雾化效果随着射流速度和撞击角度的增大而改善,这与文献[17]的雾化实验研究结果相吻合。
4.3 液膜厚度估计液膜厚度是表征雾化效果的重要参数,理论分析认为,液膜厚度与液丝/液滴的尺寸直接相关[18],因此,可以认为,液膜厚度越小,雾化效果越好。直接利用实验手段测量凝胶推进剂射流撞击后的液膜厚度较为困难,在雾化理论分析中主要应用的是Hasson等[19]于1964年提出的液膜厚度估计式
| $ H{\rm{=}}\frac{{d_{{\rm{jet}}}^2{{\sin }^3}\theta }}{{4r{{\left( {1-\cos \phi \cos \theta } \right)}^2}}} $ | (7) |
式中H为液膜厚度,djet为射流直径,2θ为撞击角,r为液膜上的点到撞击点的距离,ϕ为液膜上的点与液膜中线的夹角。式(7)的主要问题在于忽略了流体的粘性及射流速度等因素对于液膜厚度的影响。Choo等[20]对牛顿流体的研究表明,流体的粘度越大,射流撞击形成的液膜越厚;此外,在撞击角度等其它因素相同的情况下,雾化模式随着射流速度的变化而变化,因此,当射流速度不同时,液膜厚度也应该发生变化。
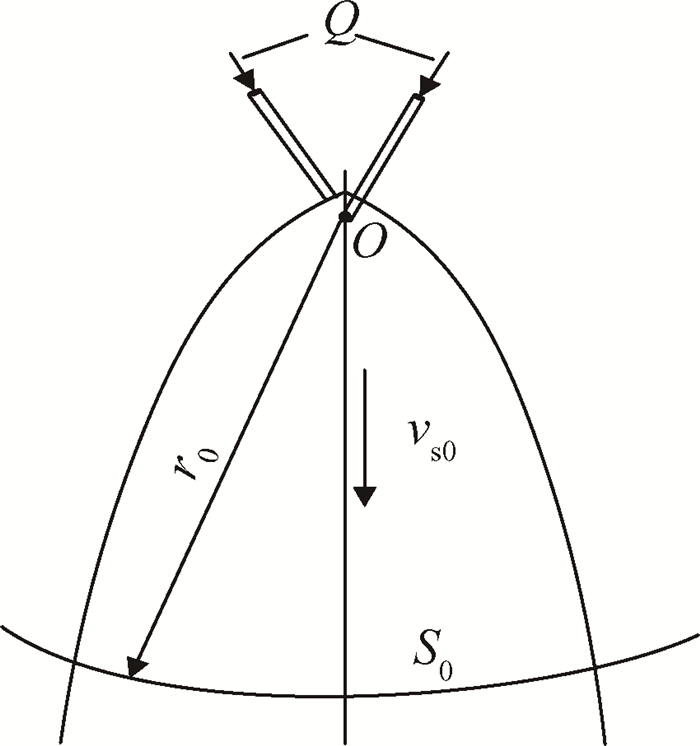
为更有效地对射流撞击形成的液膜厚度进行估计,本文以雾化图像为基础,提出了一种新的液膜厚度估算方法:如图 9所示,假设射流撞击后流体由撞击点以vs0匀速运动r0并形成了面积为S0的液膜,则液膜形成的时间为t0=r0/vs0,液膜面积S0可以通过对雾化图像的处理获得,r0内液膜的平均速度vs0通过上节方法计算,则液膜平均厚度H可通过下式估算
| $ H=\frac{{Q \cdot {t_0}}}{{{S_0}}} $ | (8) |
|
Fig. 9 Schematic diagram of liquid sheet thickness estimation |
式中Q为凝胶推进剂模拟液的管路流量。
为计算的准确性,本文对每种工况连续处理了400幅图像,并对计算出的液膜厚度进行了平均。利用上述方法计算出的SC1~SC3模拟液的液膜厚度随着射流速度及撞击角度的变化规律如图 10所示。
|
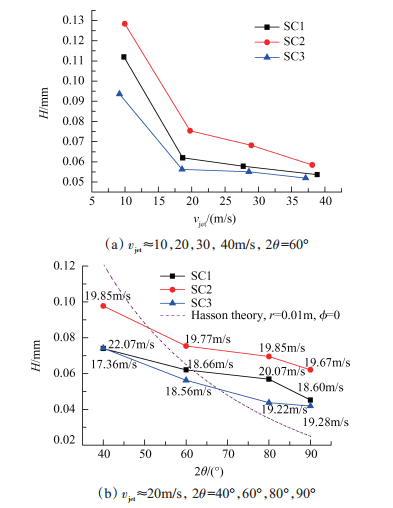
Fig. 10 Variation of liquid sheet thickness with jet velocity and impact angle |
由图 10可以得到以下结论:
(1)在本文研究范围内,射流撞击形成液膜的厚度在0.04~0.13mm;对同种凝胶模拟液,液膜厚度随着射流速度及撞击角度的增大而减小。本文计算出的液膜厚度与Hasson理论值在量值及厚度随撞击角度的变化趋势上基本一致。
(2)由图 10(a)看出,2θ=60°时,对于三种模拟液,当射流速度由10m/s提高到20m/s时,液膜厚度急剧减小,此后,随着射流速度的增大,液膜厚度减小的趋势减缓。结合雾化现象,vjet≈10m/s时,三种模拟液均为边缘封闭型雾化模式,vjet≈20m/s时,三种模拟液均为边缘敞开的雾化模式,vjet≈30、40m/s时,三种模拟液为液丝-液滴型雾化模式。因此,边缘封闭型雾化模式的液膜厚度最大;随着射流速度的增大,由边缘封闭的雾化模式向其它雾化模式发展时,液膜厚度急剧减小;在边缘敞开或液丝-液滴型雾化模式内,液膜厚度随着射流速度增大而近似呈线性缓慢减小。
(3)由图 10(a),在射流速度相同时,SC3模拟液的液膜厚度最小,其次为SC1模拟液,SC2模拟液形成的液膜厚度最大;由图 10(b)也可以得到类似结论,在撞击角度相同时,液膜厚度按照SC3,SC1,SC2的顺序逐渐增大。因此可以认为,在相同条件下,SC3模拟液雾化效果最好、SC1模拟液次之、SC2模拟液的雾化最为困难。
5 结论本文通过SIFT算法提取雾化场图像的关键点并进行精确匹配,提出了一种新型雾化场速度计算方法,并对不同工况的雾化场速度及液膜厚度进行了定量分析。主要结论如下:
(1)雾化场速度整体上随着与撞击点距离的增大而减小;撞击角一定时,雾化场平均速度随着射流速度的增大近似呈线性增大;射流速度不变时,雾化场平均速度随着撞击角度的增大而减小。这与已有文献结论相一致,充分验证了本文速度场计算方法的有效性。
(2)在本文研究范围内,雾化场平均速度与射流速度的比值vato/vjet在0.6~0.9。vato/vjet可作为雾化过程中能量转换效率的度量,用于表征雾化效果。对同一种凝胶推进剂模拟液,vato/vjet越小,能量转换效率越高,雾化效果越好。
(3)在本文研究范围内,射流撞击形成液膜的厚度在0.04~0.13mm;对同一种凝胶模拟液,液膜厚度随着射流速度及撞击角度的增大而减小。
(4)碳颗粒的添加对雾化的影响显著,当碳颗粒平均粒径相同时,碳颗粒质量分数越大,雾化效果越差;当碳颗粒质量分数相同时,粒径的增大会造成雾化过程中颗粒间刚性碰撞作用增强、胶凝剂对碳颗粒的约束作用减弱,从而雾化效果提高。
| [1] |
Hodge K, Crofoot T, Nelson S. Gelled Propellants for Tactical Missile Applications[R]. AIAA 99-2976. http://arc.aiaa.org/doi/pdf/10.2514/6.1999-2976
(  0) 0) |
| [2] |
刘虎, 强洪夫, 韩亚伟, 等. 幂律型凝胶推进剂射流撞击雾化SPH模拟[J]. 推进技术, 2015, 36(9): 1416-1425. (LIU Hu, QIANG Hong-fu, HAN Ya-wei, et al. SPH Simulation of Atomization Characteristics of Power-Law Gelled Propellant Formed by Two Impinging Jets[J]. Journal of Propulsion Technology, 2015, 36(9): 1416-1425.)
(  0) 0) |
| [3] |
Natan B, Rahimi S. The Status of Gel Propellants in Year 2000[J]. International Journal of Energetic Materials and Chemical Propulsion, 2002, 5(1-6): 172-192. DOI:10.1615/IntJEnergeticMaterialsChemProp.v5.i1-6
(  0) 0) |
| [4] |
Jayaprakash N, Chakravarthy S R. Impingement Atomization of Gelled Fuels[R]. AIAA 2003-316. http://arc.aiaa.org/doi/abs/10.2514/6.2003-316
(  0) 0) |
| [5] |
Von Kampen J, Alberio F, Ciezki H K. Spray and Combustion Characteristics of Aluminized Gelled Fuels with an Impinging Jet Injector[J]. Aerospace Science and Technology, 2007, 11: 77-83. DOI:10.1016/j.ast.2006.08.006
(  0) 0) |
| [6] |
Baek G, Kim S, Han J, et al. Atomization Characteristics of Impinging Jets of Gel Material Containing Nanoparticles[J]. Journal of Non-Newtonian Fluid Mechanics, 2011, 166(21): 1272-1285.
(  0) 0) |
| [7] |
张蒙正, 李军, 陈炜, 等. 互击式喷嘴燃烧室燃烧效率实验[J]. 推进技术, 2012, 33(1): 54-57. (ZHANG Meng-zheng, LI Jun, CHEN Wei, et al. Experiments on Combustion Efficiency for Impinging Injector Chamber[J]. Journal of Propulsion Technology, 2012, 33(1): 54-57.)
(  0) 0) |
| [8] |
Rodrigues N S, Sojka P E. A Parametric Investigation of Gelled Propellant Spray Characteristics Utilizing Im pinging Jet Geometry[R]. AIAA 2014-1184. http://arc.aiaa.org/doi/abs/10.2514/6.2014-1184
(  0) 0) |
| [9] |
陈杰, 封锋, 马虎, 等. 基于PIV的凝胶模拟液撞击雾化速度场实验研究[J]. 推进技术, 2014, 35(4): 565-569. (CHEN Jie, FENG Feng, MA Hu, et al. Experimental Study on Impinging Velocimetry of Gel Stimulants Based on PIV[J]. Journal of Propulsion Technology, 2014, 35(4): 565-569.)
(  0) 0) |
| [10] |
Arienti M, Li X, Soteriou M C, et al. Coupled LevelSet/Volume-of Fluid Method for the Simulation in Propulsion Device Injectors[R]. AIAA 2010-7136.
(  0) 0) |
| [11] |
Ma D J, Chen X D, Khare P, et al. Atomization Patterns and Breakup Characteristics of Liquid Sheets Formed by Two Impinging Jets[R]. AIAA 2011-97. http://arc.aiaa.org/doi/abs/10.2514/6.2011-97
(  0) 0) |
| [12] |
强洪夫, 韩亚伟, 王广, 等. 幂律型流体雾化SPH方法数值分析[J]. 推进技术, 2013, 34(2): 240-247. (QIANG Hong-fu, HAN Ya-wei, WANG Guang, et al. Numerical Analysis of Atomization Process of Liquid with Power Law Model Based on SPH Method[J]. Journal of Propulsion Technology, 2013, 34(2): 240-247.)
(  0) 0) |
| [13] |
Lowe D G. Object Recognition from Local Scale-Invariant Features[C]. Kerkyra: Proceedings of the 7th IEEE International Conference on Computer Vision, 1999. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=790410
(  0) 0) |
| [14] |
Lowe D G. Distinctive Image Features from Scale-Invariant Keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91-110. DOI:10.1023/B:VISI.0000029664.99615.94
(  0) 0) |
| [15] |
王梅, 屠大维, 周许超. SIFT特征匹配和差分相乘融合的运动目标检测[J]. 光学精密工程, 2011, 19(4): 892-899. (  0) 0) |
| [16] |
Heislbetz B, Madlener K, Ciezki H K. Breakup Characteristics of a Newtonian Liquid Sheet Formed by a Doublet Impinging Jet Injector[R]. AIAA 2007-5694. Breakup Characteristics of a Newtonian Liquid Sheet Formed by a Doublet Impinging Jet Injector
(  0) 0) |
| [17] |
张蒙正, 陈炜, 杨伟东, 等. 撞击式喷嘴凝胶推进剂雾化及表征[J]. 推进技术, 2009, 30(1): 46-50. (ZHANG Meng-zheng, CHEN Wei, YANG Wei-dong, et al. Atomization and Characteristics of Gelled Propellant with Impinging Injector[J]. Journal of Propulsion Technology, 2009, 30(1): 46-50.)
(  0) 0) |
| [18] |
Chojnacki K T. Atomization and Mixing of Impinging Non-Newtonian Jets[D]. Huntsville: University of Alabama-Huntsville, 1997.
(  0) 0) |
| [19] |
Hasson D, Peck R. Thickness Distribution in a Sheet Formed by Impinging Jets[J]. Aiche Journal, 1964, 10(5): 752-754. DOI:10.1002/(ISSN)1547-5905
(  0) 0) |
| [20] |
Choo Y J, Kang B S. Parametric Study on ImpingingJet Liquid Sheet Thickness Distribution Using an Interferometric Method[J]. Experiments in Fluids, 2001, 31: 56-62. DOI:10.1007/s003480000258
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

