2. 中航工业飞机强度研究所,陕西 西安 710065
2. AVIC Aircraft Strength Research Institute, Xi'an 710065, China
声波在管道内是以模态波形式传播,管道内可传播的模态波(即截通模态)的个数依赖于管道几何结构、声波频率、气流速度和管道边界的声学条件。航空发动机噪声包括单音噪声(例如转子自噪声,蜂鸣声和转静干涉噪声)和宽频噪声[1]。针对单音噪声国内研究人员从预测模型[2]、数值计算[3]和降噪[4]等进行了研究。为了研究管道内单音噪声的产生机理,国内外的研究普遍采用模态分解的方法进行研究。对于单音噪声中径向模态分析(其内部成分完全相关),从20世纪60年代开始,出现了很多实验测量方法[5~13]。其中Bolleter[5, 6]对管道模态和声功率测量给出了理论指导意见,大量研究人员用旋转耙[7, 9~13]对管道内周向模态[12]和径向模态[7, 13]及其产生机制[8]进行了实验探索对进行了实验研究。
考虑到可求解模态范围、分析结果精度、方法应用复杂度等方面,这些方法都有不同的局限性。最理想的情况是通过远场测量来实现径向模态分解[14],因为这种实验方案在实际测量中容易实现且不受环境尺寸的限制。但解析模型通常对发动机几何结构进行了简化处理,这就会造成计算误差,而且通过远场测量来实现径向模态分解需要对发动机进口和远场之间的声传递函数进行数值计算,研究表明这种计算非常耗时。现如今对于中高频处的声场进行径向模态分解通常采用的是在管道内布置大量传感器[15],通过对测量的声压数据进行反方法处理得到管道内径向模态分布结果。德国宇航院(DLR)成功地利用该方法对风扇[10, 16]、低压压气机[17]、低压涡轮[18]的管道内单音进行了测量。Sutliff[13]和Enghardt[18]用旋转径向耙对管道内声场进行测量,这种阵列的好处就是可以直接测量出模态波在径向方向的分布,但安放在上游时其尾迹会和原来流场进行干涉而对声场造成污染。这种情况在用轴向阵列[17]时会得到改善,但轴向阵列需要测量段足够长用以安装更多的传声器在机匣壁面上。
为了研究径向耙和轴向阵列在模态分解中的优劣,Tapken[19]在风扇下游分别安装了旋转径向耙和轴向阵列。结果表明两种阵列分解出的模态结果总体上符合的很好,结果中的小偏差一方面是由两种阵列构建出的系数矩阵不同引起的,另一方面是因为两种阵列对管道内气流的敏感性不同引起的。NASA[20]用两个旋转耙对管道声场进行了测量,利用两个耙分解出的周向模态相位差异,将管道内顺流和逆流传播的模态分辨出来。研究还指出如果其中一个耙采集到“截止”模态时,需要在声学模型中将“截止”模态考虑进去,以防止这部分能量被强制叠加到其它模态中。佛罗伦萨大学[21]和DLR[22]的研究表明径向耙和轴向阵列测量出的主导模态和其它模态的相对量级大小结果相同。并且随着试验件工作点变化,两种阵列捕捉到的单音变化规律也是类似的。
径向模态分解其目的是用反方法对所研究的声场进行完全的径向分解,这可以通过对连接测量声压和径向模态幅值的系数矩阵求逆来实现。在绝大多数研究中,测量的声压点个数要大于未知模态幅值的个数,即变成一个线性二次拟合过程[23, 24]。适定的系统其解是唯一且稳定的,而病态系统求解出的结果不稳定且有歧义(强烈依赖于信号的信噪比)。系统病态一方面是因为理论模型不适用于所研究的问题造成的;另一方面是因为系数矩阵病态导致的。后者通常是因为传声器测点位置选择不恰当引起的。
为了探索不同阵列设计方案在管道内单音测量上的局限性,本文首次通过数值方法研究了径向耙和轴向阵列在径向模态分解上优缺点。通过对系数矩阵条件数分析研究了阵列轴向间距对模态分解的影响,并利用在人造声场中叠加随机扰动研究了不同阵列在模态分解时的误差传递特性,从而给单音分解以理论指导。基于此理论分析结果,设计了旋转轴向阵列测量装置对风扇管道内的顺流和逆流传播的模态波结构进行测量分析。
2 实验对象和测量设备 2.1 风扇试验台实验对象是西北工业大学叶轮机械气动力学和气动声学实验室的单级低速轴流风扇试验件NPU-Fan。试验件的设计参数如表 1所示。风扇管道内转静干涉模态截通特性如表 2所示。
|
|
Table 1 Design parameters of fan |
|
|
Table 2 Rotor-stator interaction modes of NPU-Fan |
其中BPF表示叶片通过频率。为了更精确地测量管道内声场特性,消除不必要的噪声污染,实验的声学环境尤为重要。本次实验对现有的风扇试验台进行了必要的声学实验条件改善,主要包括:
(a)将风扇进口段、声学测量段放置于飞机强度所(ASRI)的半消声室内部,目的是为了减少和消除外部噪声反射到风扇进口测量段;
(b)增加安装风扇排气吸声管道(图 1黑色方框所示),目的是为了减少排气段产生的额外噪声,并消除排气噪声向进口管道的辐射。
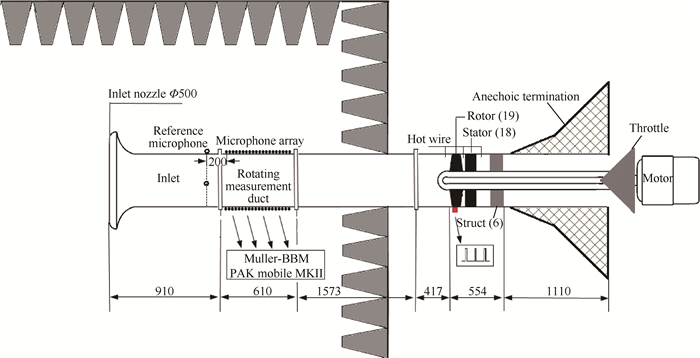
|
Fig. 1 Diagram of fan rig(mm) |
风扇试验台简图如图 1所示,声学测量装置安放在风扇进口段,距转子叶尖前缘1.90m。实验中采用旋转阵列来对管道声场进行测量,即传声器阵列安装在旋转机匣上(图 2左侧所示)。这样做的好处是可以通过安装少量的传声器来获得更多位置处的声压信息。实验中安装了2排轴向阵列,每排阵列由14个等间距分布的传声器组成,轴向间距为Δx=2.4 cm,2排阵列周向相隔180°。为了达到周向定角度声学测量的目的,旋转测量段设计成由步进电机驱动,步进电机单次脉冲带动齿轮旋转的角度是固定的。本次实验中周向每旋转6°进行一次测量。实验中在旋转测量段上游20 cm处放置了两个位置固定的传声器,其轴向位置如图 1所示。周向位置如图 2右侧所示,两者相隔100°。
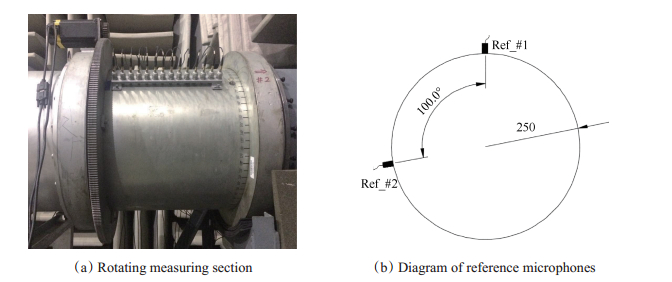
|
Fig. 2 Noise measurement device |
对于旋转测量,由于各周向测点位置的声场信息不是同时采集,因此各周向测量位置处的声学信号之间的相位差不是恒定的。因此虽然旋转阵列相较于固定阵列优势明显,但其难点是保证各测点处的声压信号相位差稳定。本次实验中为了保证每次测量时对应的转子转动位置相同,实验中在转子前缘的机匣壁面安装了红外传感器(图 1红色所示),反射胶纸放置于轮毂处。实验中声学信号和红外信号同时由Müeller BBM MK Ⅱ数据采集系统采集,采样频率是fs=16.384kHz,每个测点采集时间是12.7s。
3 单音噪声测试方法 3.1 管道声学理论在以下假定条件下:
(a)不可压缩介质,等熵流动,并且忽略温度梯度;
(b)轴向和周向平均速度分布以及管道截面形状在轴向方向保持不变;
(c)没有径向速度分布;
(d)周向和轴向流速不随时间发生变化;
(e)介质的温度和密度在空间和时间上都是不变的。
圆形/环形管道内声学传播方程可以写成
| $ \frac{1}{{{c^2}}}\frac{{{{\rm{D}}^2}p}}{{{\rm{D}}{t^2}}} - \frac{{{\partial ^2}p}}{{\partial {x^2}}} - \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial p}}{{\partial r}}} \right) - \frac{1}{{{r^2}}}\frac{{{\partial ^2}p}}{{\partial {\theta ^2}}} = 0 $ | (1) |
式中c是声速,p是声压。对于声场在圆柱或环形的硬壁管道内传播,式(1)可以得到一种数值解,对于某个频率可以由模态波的线性叠加得来[4]。
| $ p\left( {x,r,\varphi ,t} \right) = \sum\limits_{m = - \infty }^\infty {\sum\limits_{n = 0}^\infty {\left( {A_{mn}^ + {{\rm{e}}^{ - {\rm{i}}k_{{\rm{mn}}}^ + x}} + A_{mn}^ - {{\rm{e}}^{{\rm{i}}k_{{\rm{mn}}}^ - x}}} \right){\psi _{mn}}\left( r \right){{\rm{e}}^{{\rm{i}}m\varphi }}{{\rm{e}}^{{\rm{i}}\omega t}}} } $ | (2) |
式中ω是角频率,Amn±表示模态振幅,上标±表示模态传播方向为顺流(Downstream)和逆流(Upstream),在本文其它位置也是指传播方向。ψmn(r)表示模态形状函数,定义为
| $ {\psi _{mn}}\left( r \right) = \frac{1}{{\sqrt {{F_{mn}}} }}\left( {{J_m}\left( {{\sigma _{mn}}\frac{r}{R}} \right) + {Q_{mn}}{Y_m}\left( {{\sigma _{mn}}\frac{r}{R}} \right)} \right) $ | (3) |
| $ {f_{mn}}\left( r \right) = {J_m}\left( {{\sigma _{mn}}\frac{r}{R}} \right) + {Q_{mn}}{Y_m}\left( {{\sigma _{mn}}\frac{r}{R}} \right) $ | (4) |
| $ {F_{mn}} = \left[ {\left( {1 - \frac{{{m^2}}}{{\sigma _{mn}^2}}} \right){f_{mn}}{{\left( R \right)}^2} + \left( {{\eta ^2} - \frac{{{m^2}}}{{\sigma _{mn}^2}}} \right){f_{mn}}{{\left( {\eta R} \right)}^2}} \right] $ | (5) |
η是无量纲半径,σmn是模态(m, n)的特征值。对于非环形管道Qmn为零,Fmn是归一化系数,其定义是公式(5)。模态特征函数满足
| $ \frac{1}{{{\rm{ \mathsf{ π} }}{R^2}}}\int\limits_0^{2{\rm{ \mathsf{ π} }}} {{{\rm{e}}^{{\rm{i}}\left( {m - \mu } \right)\varphi }}} \int\limits_{\eta R}^R {{\psi _{mn}}\left( r \right){\psi _{\mu \nu }}\left( r \right)r{\rm{d}}r{\rm{d}}\varphi } = {\delta _{m\mu }}{\delta _{n\nu }} $ | (6) |
轴向波数kmn±依赖于模态(m, n)的特征值以及自由场中的波数k=ω/c,定义为
| $ k_{mn}^ \pm = k\frac{{ - Ma \pm {\alpha _{mn}}}}{{{\beta ^2}}} $ | (7) |
| $ {\alpha _{mn}} = \sqrt {1 - {{\left( {\frac{{\beta {\sigma _{mn}}}}{{kR}}} \right)}^2}} $ | (8) |
| $ \beta = \sqrt {1 - M{a^2}} $ | (9) |
式中Ma是气流轴向马赫数,在这里定义为U/c。当kmn±是实数时表示模态波可以沿着管道传播,相应的模态截通频率定义为
| $ {f_{c,mn}} = \frac{{{\sigma _{mn}}}}{{2{\rm{ \mathsf{ π} }}R}}c\sqrt {1 - M{a^2}} $ | (10) |
可知其与气流马赫数、管道轮毂比、管道参数相关。根据模态幅值可以通过公式(11)计算出模态声功率
| $ P_{mn}^ \pm = \frac{{{\rm{ \mathsf{ π} }}{R^2}}}{{\rho c}}\frac{{{\alpha _{mn}}{\beta ^4}}}{{{{\left( {1 \mp {\alpha _{mn}}Ma} \right)}^2}}}{\left| {A_{mn}^ + } \right|^2} $ | (11) |
本文的重点是应用模态分解方法将完全相关的模态声场分解成各个模态组成部分。对于近代的发动机,尤其是发动机短舱,这个实验方法有很大的应用价值。当模态截通时,它们就可以携带能量,并可以从管道内声源处辐射到远场。模态分解方法基于一个线性方程组,系统的建立依赖于将目标物理量(模态幅值)和测量的声压联系起来的声学模型。
模态分解方法分为两部分:周向模态分解和径向模态分解。
3.2.1 周向模态分解公式(1)的解(公式(2))可以简化成
| $ p\left( {x,r,\varphi } \right) = \sum\limits_{m = - \infty }^\infty {{A_m}\left( {x,r} \right) \cdot {{\rm{e}}^{{\rm{i}}m\varphi }}} $ | (12) |
其中周向模态幅值Am(x, r)表示
| $ {A_m}\left( {x,r} \right) = \sum\limits_{n = 0}^\infty {\left( {A_{mn}^ + \cdot {{\rm{e}}^{ {\rm{i}}k_{mn}^ + x}} + A_{mn}^ - \cdot {{\rm{e}}^{{\rm{i}}k_{mn}^ - x}}} \right) \cdot {\psi _{mn}}\left( r \right)} $ | (13) |
通常周向模态幅值可以通过简单的周向离散傅里叶变换(DFT)得到
| $ {A_m}\left( {{x_0},{r_0}} \right) = \frac{1}{{{N_\varphi }}}\sum\limits_{l = 0}^{{N_\varphi } - 1} {p\left( {{x_0},{r_0},{\varphi _l}} \right) \cdot {{\rm{e}}^{-{\rm{i}}m{\varphi _l}}}} $ | (14) |
其中离散傅里叶变换是基于固定轴向和半径位置(即(x0, r0)=const)的Nφ个周向测点位置的声压频谱计算得来,这Nφ个测点沿周向是等角度分布。根据奈奎斯特理论,为了求解模态时不产生混淆,最高阶周向模态阶数mmax和周向测点数Nφ需满足
| $ \frac{1}{2}\frac{{2{\rm{ \mathsf{ π} }}}}{{{m_{\max }}}} > \Delta \varphi = \frac{{2{\rm{ \mathsf{ π} }}}}{{{N_\varphi }}} \Rightarrow {m_{\max }} < \frac{{{N_\varphi }}}{2} $ | (15) |
也就是说周向阶数为mmax的模态可以通过一圈传声器信号(其周向角度间距小于2π mmax的一半)计算出来,且没有混淆。
原则意义上,仅对一个轴向位置或者径向位置的周向模态进行分解是没有多大意义的,也不能给出定量的结论。但是,多排或多个径向位置的周向模态分解可以得到管道内更细节的声波结构—径向模态,这将在下小节叙述。
3.2.2 径向模态分解对于给定的阵列布置方案,其中包含Nx个轴向测点位置或Nr个径向测点位置,每个位置处都有Nφ个周向等角度安装的传声器。各轴向或径向位置处截通的周向模态可以通过上节介绍的方法求解出来,而各位置(xj, rk)处的m阶周向模态可以表示成由多个径向模态组成
| $ {\mathit{\boldsymbol{A}}_m}\left( {{x_j},{r_k}} \right) = \sum\limits_{n = 0}^{{N_n}\left( m \right)} {{\psi _{mn}}\left( {{r_k}} \right)\left( {A_{mn}^ + {{\rm{e}}^{{\rm{i}}k_{mn}^ + {x_j}}} + A_{mn}^ - {{\rm{e}}^{{\rm{i}}k_{mn}^ - {x_j}}}} \right)} $ | (16) |
由此可以组成一个线性系统
| $ {\mathit{\boldsymbol{A}}_m} = {\mathit{\boldsymbol{W}}_m} \cdot \mathit{\boldsymbol{A}} $ | (17) |
其中Am是测量的周向模态幅值向量,其维度为Nx∙Nr × 1,Wm是模态的系数矩阵,其维度是Nx∙Nr × 2(Nn(m)+ 2),而A是径向模态幅值向量,其维度是2∙(Nn(m)+ 2)× 1。最小二乘拟合方法可以用来求解方程(17),从而得到截通的各个径向模态的幅值信息。求解过程如下
| $ \mathit{\boldsymbol{A}} = {\left[ {\mathit{\boldsymbol{W}}_m^{\rm{H}}{\mathit{\boldsymbol{W}}_m}} \right]^{ - 1}}\mathit{\boldsymbol{W}}_m^{\rm{H}}{\mathit{\boldsymbol{A}}_m} = \mathit{\boldsymbol{W}}_m^ + {\mathit{\boldsymbol{A}}_m} $ | (18) |
其中Wm+是系数矩阵Wm的伪逆矩阵,矩阵上标H表示共轭转置。方程(17)的可解性、稳定性以及系统的误差传递特性和方阵WmHWm的条件数密切相关。其条件数决定于多种因素:模态截通个数、频率、轮毂比、气流参数以及阵列设计形状等。因而通过条件数分析对模态分解进行质量评估变得很有必要。
3.2.3 模态分解质量评估径向模态分解其本质是一种经典的反问题。可以将问题分解成两部分:DFT和随后的最小二乘拟合。声压信号的精度与周向模态幅值准确度之间的关系很简单。但各径向模态幅值精度与周向模态幅值准确度之间的关系就变得很复杂。原理上,计算精度与矩阵Wm的条件数κ(w)有关。它决定了方程系统Wm的误差传递系数的上限
| $ \frac{{\left\| {{{\tilde A}_{mn}}} \right\|}}{{\left\| {{A_{mn}}} \right\|}} \le \kappa \left( w \right)\frac{{\left\| {{{\tilde A}_m}} \right\|}}{{\left\| {{A_m}} \right\|}} $ | (19) |
其中波浪字符~分别表示周向模态幅值Am和径向模态幅值Amn向量的扰动量。‖*‖表示欧几里德范数。如公式(19)所示,如果κ(w)=1,那么输入信号摄动经过系统传递到输出信号时也基本不变。当输入的幅值误差为10%时,那么通过系统后输出信号幅值的误差最大可到10%,但这种情况的前提是系统Wm是对角矩阵。对于实际操作中,方程的个数要大于未知数的个数,即超定系统。通过最小二乘拟合,最终传递出去的误差会更小。
为了研究实验中小的测量误差在系统中对最终输出(也就是模态幅值)的影响,这里用数值的方式进行模拟研究。通常来讲,测量误差分为系统误差和随机误差,但这里仅考虑随机测量误差的影响,数值中加入的随机误差满足高斯分布。
图 3给出了数值模拟中各个步骤的流程简图:
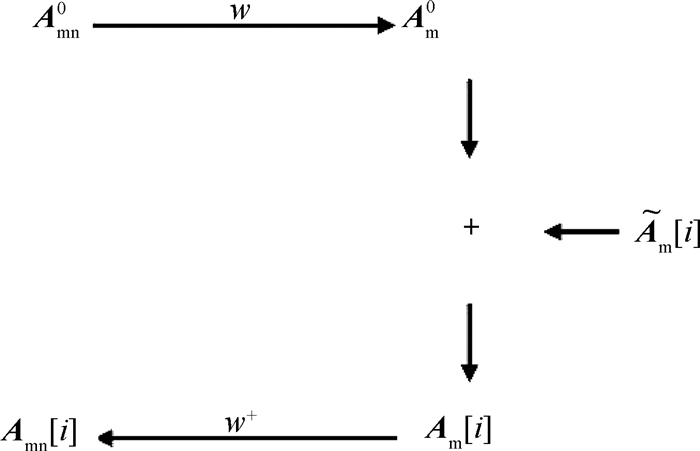
|
Fig. 3 Schematic illustration of the computer simulation |
(1)基于给定的径向模态幅值Amn0,可以数值构造出不同测点位置处,即(xj, rk) j=1, …, Nx; k=1, …, Nr处的周向模态幅值Am0。
(2)对于第ith次测量,叠加到位置(xj, rk)处的周向模态幅值摄动定义为
| $ {{\tilde A}_m}\left( {{x_j},{r_k},\left[ i \right]} \right) = {\sigma _{{A_m}}}{a_{jk}}\left[ i \right]{{\rm{e}}^{{\rm{i}}{b_{jk}}\left[ i \right]2{\rm{ \mathsf{ π} }}}} $ | (20) |
其中σAm是周向模态幅值的标准偏差,ajk[i]和 bjk[i]都是实数,它们对时间的依赖关系服从高斯分布并分别在[0, 1]均衡分布。
(3)对于每次测量i,径向模态幅值Amn[i]可以通过求解伪逆矩阵Wm+得到。
经过Navg次平均后,计算的准确性可以通过求解公式(19)或者计算每个径向模态的标准偏差σAmn来确定。
4 阵列设计优化通过上节介绍可知,阵列设计形状对求解的精度有很重要的影响。本文研究了4种阵列设计方案(如图 4所示),阵列用前缀A表示,不同方案用拉丁字母加以区分。通常实验测量段都设计在风扇进口段,因此四种阵列的轮毂比都设为η=0,其中A-Ⅰ和A-Ⅲ方案中传声器总个数Nx∙Nr=14而A-Ⅱ和A-Ⅳ方案中传声器总个数Nx∙Nr=24,其详细说明如下:
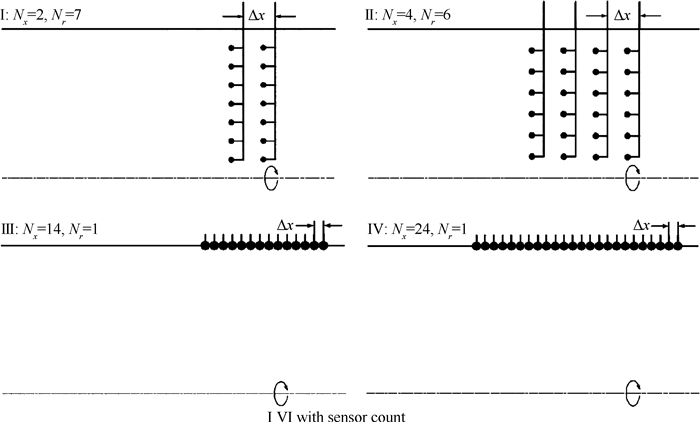
|
Fig. 4 Sensor arrangements Ⅰ-Ⅵ with sensor count NxNr = 14(left), NxNr = 24(right) |
(1)阵列方案A-Ⅰ由径向耙式阵列组成,轴向测量位置Nx=2。每个径向阵列都有Nr个等径向间距排布的传声器组成,其径向间距Δr和径向位置rj定义为
| $ {r_j} = j\Delta r,\Delta r = \frac{R}{{{N_r} + 1}} $ | (21) |
(2)阵列方案A-Ⅱ由四排径向阵列组成,其中Nx=4个轴向测量位置是等间距的,即Δx=const,每个径向阵列含有Nr个等Δr分布的传感器。径向位置和间距Δr定义与A-Ⅰ相同,都依照公式(21)。
(3)阵列方案A-Ⅲ由环壁面的麦克风阵列组成,轴向有Nx个等间距布置的测点,轴向间距为Δx。径向测量位置Nr=1。
(4)阵列方案A-Ⅳ与Ⅲ类似,都是在外机匣壁面上布置传声器,只是总的传声器个数不同。对于所有阵列方案,其轴向测点位置数Nx或者径向测点数Nr都是固定的,其中方案A-Ⅰ和A-Ⅲ由相同个数Nx∙Nr=14的传声器组成,方案A-Ⅱ和A-Ⅳ的传声器个数Nx∙Nr=24。
它们区别在于一种是轴向环壁面布置的传声器阵列,另一种是径向耙式阵列。因此余下惟一一个四种阵列的公用参数Δx。下面将研究阵列间距Δx对矩阵条件数的影响,以及最佳布置方案。考虑到周向测点数Nφ,模拟中假设阵列都安装在旋转测量段上,测量段可以沿周向定角度旋转360°。所有的模拟中都假设周向有足够多的测点,以满足任意周向模态阶数的模态分解都满足奈奎斯特定理(公式(15))。基于数学原理,径向阵列与轴向阵列相比有优势。因为参考公式(3),径向阵列中不同径向位置处测量的模态幅值不同,而轴向阵列中不同轴向位置处模态幅值相同但其相位有差异。因此模态分解中基于幅值不同(径向阵列)的算法比基于相位不同(轴向阵列)的算法数值更加稳定。但对于实际实验测量,例如在风扇进口段对管道内声场进行测量,径向传声器阵列中一个或多个传感器的尾迹与声源(例如转子)进行干涉,这会改变原始的声场结构,并激发出额外的噪声。尤其对于直径尺寸小的实验台,耙式阵列会引起气流堵塞,这实质上会改变叶轮机械的工作状态点。对于轴向阵列(例如A-Ⅲ和A Ⅳ),这两个缺点都可规避。数值研究的频率范围都是0≤kR≤35,最多可截通11个径向模态,这些模态分别向顺流和逆流方向传播。模拟中首先计算出图 5中四种阵列其对应的条件数结果,在给定误差限后,可以得到对应于各个阵列的最佳轴向间距Δxopt,使得模态分解可以在既定的误差限范围内推进到最大频率max(kR)处。
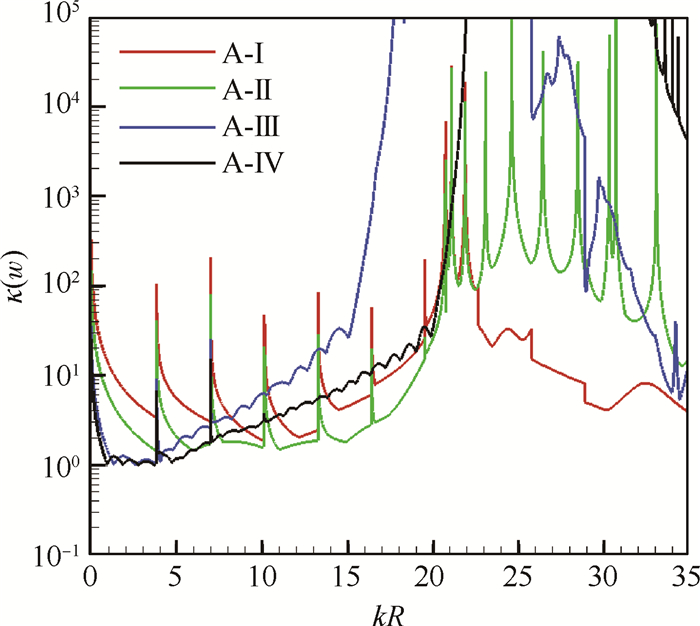
4.1 m=0模态条件数图 5分别给出了四种阵列设计方案在周向模态m=0时条件数κ(w)的结果。选择对模态m=0进行分析是因为该模态相比其它模态可以截通更多的径向模态。结果表明条件数κ(w)非常依赖于阵列的轴向间距Δx/R以及频率kR。对比四种阵列的条件数结果可以发现较大条件数对应的频率kR和Δx/R大体上是一致的,而A-Ⅰ阵列看起来更优于另外三种阵列。深入研究后可以发现较大的条件数κ(w)是由于阵列对轴向方向的声波相位差测量不足导致的。不同于径向模态特征函数的正交性(公式(6)所示),轴向波数并不正交,因此较大条件数会出现在
| $ \begin{array}{l} \left( {{\alpha _{mn}} - {\alpha _{m\nu }}} \right)k\Delta x = s \cdot 2{\rm{ \mathsf{ π} }}\\ \left( {{\alpha _{mn}} + {\alpha _{m\nu }}} \right)k\Delta x = s \cdot 2{\rm{ \mathsf{ π} }} \end{array} $ | (22) |

|
Fig. 5 Condition number κ(w) of model matrix Wm using sensor arrangements A-Ⅰ to A-Ⅳ |
式中s为整数。原理上随着频率增加,公式(21)对应的组合(kR和Δx/R)个数增加,这是因为截通的径向模态波个数Nrad增加以及模态的截通因子αmn趋近于1导致的。然而,四种阵列关于公式(22)的关联关系是不同的,更准确的说,它依赖于Nr/Nrad。
(1)当Nr/Nrad ≥ 1时,径向模态特征函数正交特性被很好的模拟出来,因此n≠ν的模态组合对条件数κ(w)没有贡献。因而这种条件下,公式(22)只和n=ν径向模态相关,这样较大的矩阵条件数只和少量的组合有关(kR和Δx/R)。这种情况对应于A-Ⅰ中kR<kR0, 6和A-Ⅱ中kR<kR0, 5。
(2)当Nr/Nrad<1时,根据公式(22),更多的n≠ν模态组合会对条件数κ(w)产生贡献,这样就会导致高条件数对应的组合(kR和Δx/R)变多。这种情况对应于阵列A-Ⅲ和A-Ⅳ(如图 6所示)。
|
Fig. 6 Condition number of four arrays using the optimized sensor interval Δx= Δxopt |
当频率接近模态截通频率时,轴向波数kmn±接近为0(当Ma≪1时),这时模态的波长接近无穷大,对于这种模态理论上需要在轴向很远的间隔处布置传声器才能进行模态测量。对于A-Ⅰ和A-Ⅱ方案,其轴向测量点数少,当Δx较小时,就会导致一个严重的问题。如图 5所示,在kR ≈ fc, mn时A-Ⅰ和A-Ⅱ的条件数会激增。图 6给出了最佳轴向间距Δxopt时四种阵列的条件数结果。结果表明径向耙在低频时表现不好,也就是在模态截通比较低时条件数较大,尤其是在频率靠近截通频率时,条件数会增加两个量级左右。而且用于安装径向传声器的支撑部件产生的尾迹会影响到声压信号采集进而降低采集信号的信噪比。因此轴向阵列在实际应用中变得很有优势,下节将对轴向阵列进行细致研究。
4.2 m=0模态相对精度和最佳轴向间距矩阵条件数κ(w)只能反映模态分解时整体的误差上限,为了更深入研究,这里用公式(19)推导出的相对精度来研究模态分解的可靠性,其定义是
| $ {\left\| {{{\tilde A}_{mn}}} \right\|_{{\rm{rel}}}}: = \frac{{\left\| {{{\tilde A}_{mn}}} \right\|}}{{\left\| {{A_{mn}}} \right\|}}\frac{{\left\| {{A_m}} \right\|}}{{\left\| {{{\tilde A}_m}} \right\|}} $ | (23) |
计算中
数值模拟按照图 3所示的步骤进行,模态幅值以及加入的扰动值设置如表 3所示。其中顺流传播的模态为85dB,逆流传播的模态为75dB,这里仅研究轴向阵列,即A-Ⅳ类型的阵列。
|
|
Table 3 Design parameters of artificial sound fields |
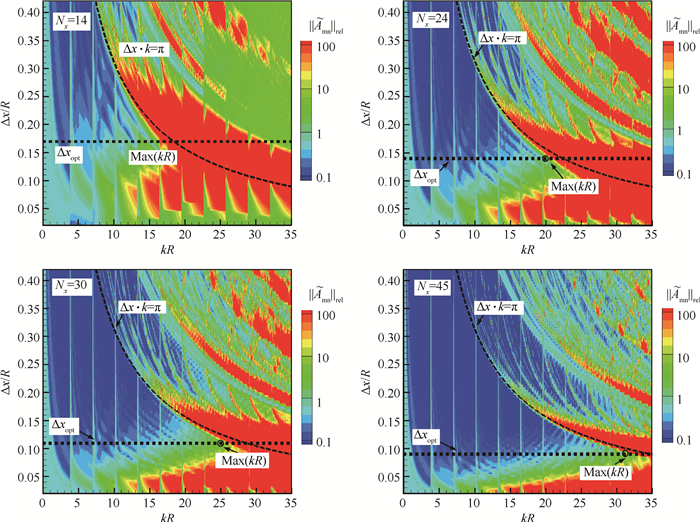
图 7给出不同个数传声器组成的轴向阵列的相对精度结果可以看出与条件数的结果类似,
|
Fig. 7 Relative accuracy results of four kinds of axial arrays |
|
|
Table 4 Optimum sensor interval and maximum resolving frequency |
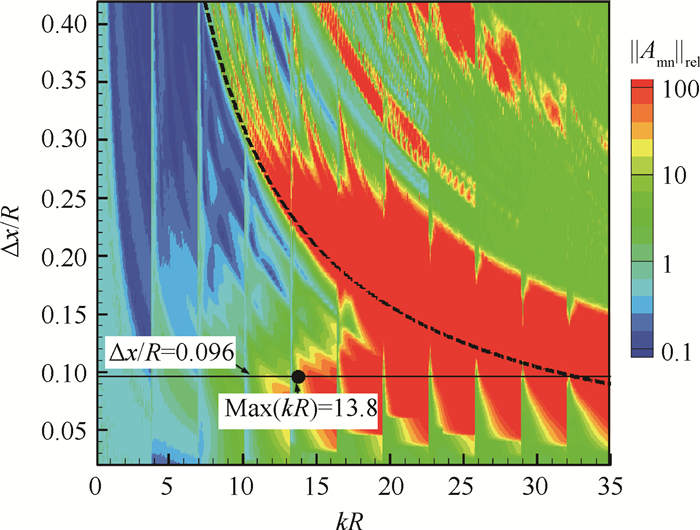
前面章节通过数值方法研究了不同阵列设计方案对管道模态分解精度的影响。结果表明轴向阵列在低频时优于径向耙式阵列。因此在实验设计中采用了旋转轴向阵列对管道内声场进行测量。阵列由14个等间距的传声器组成。根据实验中阵列的真实轴向间距Δx/R=0.096,图 8给出了
|
Fig. 8 Relative accuracy of experimental realistic array |
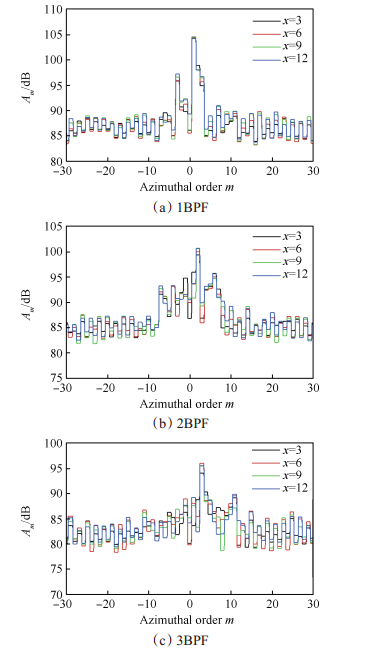
图 9展示的是公式(14)计算出的叶片通过频率BPF及其谐频处的各阶周向模态功率分布结果,用Am表示,单位为dB。根据奈奎斯特采样定理,60个周向测点可以分辨的周向模态范围是-30到+30。实验中总共测量了14个轴向位置的声压信息,分解出的周向模态结果按照气流方向分别用x=1~14依次标识,为了更清晰和简明地展示单音噪声模态识别结果,这里仅给出了4个轴向位置的周向模态结果,即:x=3, 6, 9, 12。可以看出不同频率处,截通的模态在功率分布中占主导地位,这与理论是相符的。其中转静干涉模态在各转子通过频率处能量级最大,1BPF处m=1模态的声功率为105.4dB,2BPF处m=2模态的声功率为100.5dB,3BPF处m=3模态的声功率为95.5dB。由于各轴向位置测点采集的声压是由不同模态声波以复数形式叠加而成的,因此各个轴向位置测量出的模态幅值会有所区别。图中可以看出主导模态受此影响最小,其它非主导模态因阶数m的不同受影响程度有所区别,其中最大偏差可达4dB。这从侧面也反映出在管道单音噪声测量中,仅进行周向模态分解是远远不足的,需要进一步分析其径向模态信息。
|
Fig. 9 Sound power distribution of circumferential modes at BPFs |
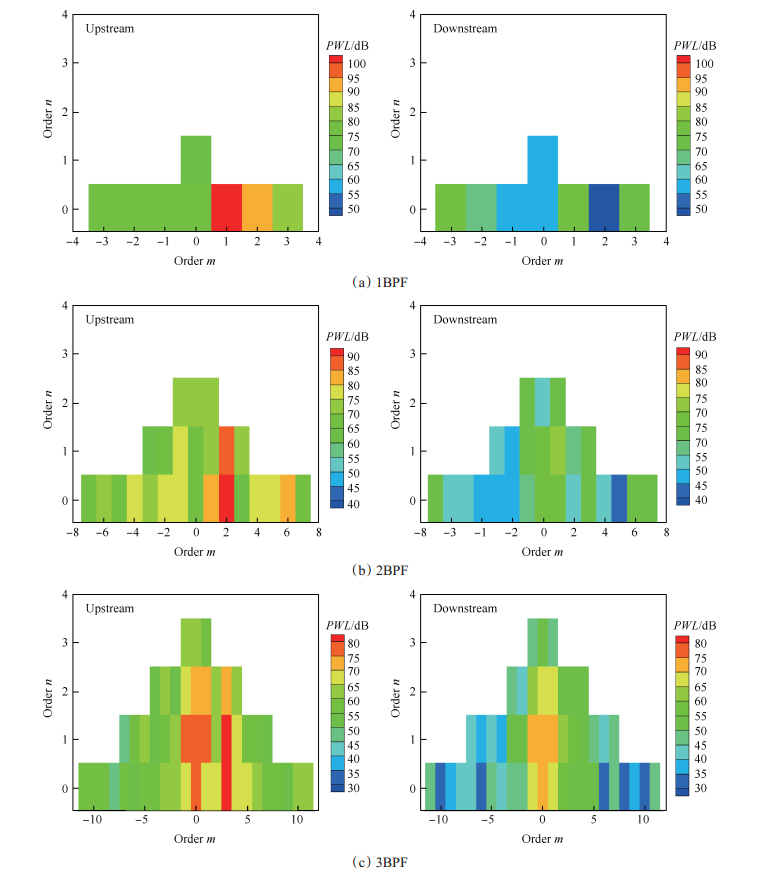
图 10给出了BPF及其谐频处向上游和下游传播的径向模态声功率结果,用PWL表示,单位为dB。向上游传播(Upstream)的模态波能量高于向下游传播(Downstream)的模态波。对于在管道进口进行声学测量,向上游传播的声波是入射波,而向下游传播的是反射波,图中可以看出入射波比反射波高10dB左右。在向上游传播的模态声功率结果中(图 9左侧),可以看出转静干涉模态是其主导模态(转静干涉模态阶数参考表 2),比其它模态高出10dB以上。在3BPF时,转静干涉模态主导性减弱,平面波增强,尤其是(0,1)模态。对比各BPF处的主导模态可知,随着谐波数增加,主导模态的声功率减弱,例如1BPF处的(1,0)模态声功率为104.8dB,而2BPF处的(2,0)模态声功率为93.9dB。在向下游传播的模态声功率结果中(图 9右侧),可以发现模态分布并没有明显的规律,反射声波中已不受风扇的影响。实验测量的模态信息可以用来指导管道声衬设计或者通过声传播模型推算出远场的噪声结果。
|
Fig. 10 Modal sound power propagating upstream and downstream at different BPF |
(1)通过系数矩阵条件数分析,研究了不同阵列在径向模态分解方面的适用性和局限性,以及在模态分解过程的误差传递特性。数值和实验结果表明径向耙不适合研究低频噪声,尤其是当频率接近模态截通频率时其传递函数的条件数大于100,轴向阵列在低频时表现良好,其条件数小于10。
(2)利用旋转轴向阵列对管道模态进行分解时,其求解精度严重依赖于测点的轴向间距。当测点个数给定时,轴向间距和最大求解频率在一定范围内成反比规律。
(3)通过改变轴向阵列的测点间距,可以提高模态分解时的精度并拓宽可求解的频率范围。当给定测点间距,在一定误差限内可以确定出模态分解频率范围。
(4)实验研究结果表明NPU-Fan的入射声波的能量比反射声波大,其差别最大可达10dB。在入射声波中,转静干涉模态是叶片通过频率及其谐频处的主导模态。
| [1] |
乔渭阳. 航空发动机气动声学[M]. 北京: 北京航空航天大学出版社, 2010.
(  0) 0) |
| [2] |
王良锋, 乔渭阳, 纪良, 等. 风扇进口噪声预测模型的改进[J]. 推进技术, 2015, 36(2): 226-231. (WANG Liang-feng, QIAO Wei-yang, JI Liang, et al. An Improved Prediction Model for Fan Inlet Noise[J]. Journal of Propulsion Technology, 2015, 36(2): 226-231.)
(  0) 0) |
| [3] |
乔渭阳, 李文兰. 飞机螺旋桨噪声的数值计算[J]. 推进技术, 1992(5): 44-49. (QIAO Wei-yang, LI Wen-lan. The Numerical Calculation of Aircraft Propeller Noise[J]. Journal of Propulsion Technology, 1992(5): 44-49.)
(  0) 0) |
| [4] |
何敬玉, 李晓东. 锯齿型喷口抑制热喷流噪声的实验研究[J]. 推进技术, 2015, 36(2): 167-174. (HE Jing-yu, LI Xiao-dong. Investigation into Hot Jet Noise Reduction Mechanisms of Chevron Nozzles[J]. Journal of Propulsion Technology, 2015, 36(2): 167-174.)
(  0) 0) |
| [5] |
Bolleter U, Crocker M J. Theory and Measurement of Modal Spectra in Hard-Walled Cylindrical Ducts[J]. Journal of the Acoustical Society of America, 1972, 51: 1439-1447. DOI:10.1121/1.1912994
(  0) 0) |
| [6] |
Bolleter U, Cohen R, WANG J. Design Considerations for an in-Duct Sound Power Measuring System[J]. Journal of Sound and Vibration, 1973, 28(4): 669-685. DOI:10.1016/S0022-460X(73)80142-7
(  0) 0) |
| [7] |
Moore C J. Measurement of Radial and Circumferential Modes in Annular and Circular Ducts[J]. Journal of Sound and Vibration, 1979, 62(2): 235-256. DOI:10.1016/0022-460X(79)90024-5
(  0) 0) |
| [8] |
Joppa P D. Acoustic Mode Measurements in the Inlet of a Turbofan Engine[J]. Journal of Aircraft, 1987, 24(9).
(  0) 0) |
| [9] |
Heidelberg L, Hall D G. Inlet Acoustic Mode Measurements Using a Continuously Rotating Rake[J]. Journal of Aircraft, 1996, 32(4).
(  0) 0) |
| [10] |
Holste F, Neise W. Noise Source Identification in a Profane Model by Means of Acoustical Near Field Measurements[J]. Journal of Sound and Vibration, 1997, 203(4): 641-665. DOI:10.1006/jsvi.1996.0890
(  0) 0) |
| [11] |
Enghardt L, Zhang Y, Neise W. Experimental Verification of a Radial Mode Analysis Technique Using WallFlush Mounted Sensors[C]. Berlin: 137th Regular Meeting of the Acoustical Society of America, 1999. https://www.researchgate.net/publication/224801936_Experimental_verification_of_a_radial_mode_analysis_technique_using_wall-flush_mounted_sensors
(  0) 0) |
| [12] |
Lan J H, Premo J W, Sutliff D L. Inlet Mode Measurements with an Inflow Control Device Microphone Array [R]. AIAA 2002-2563. https://arc.aiaa.org/doi/abs/10.2514/6.2002-2563
(  0) 0) |
| [13] |
Sutliff D L. Rotating Turbofan Duct Mode Measurement System[R]. NASA-TM-213828, 2005. http://www.researchgate.net/publication/24339817_Rotating_rake_turbofan_duct_mode_measurement_system
(  0) 0) |
| [14] |
Farassat F, Nark D M, Thomas R H. The Detection of Radiated Modes from Ducted Fan Engines[R]. AIAA 2001-2138. https://arc.aiaa.org/doi/abs/10.2514/6.2001-2138
(  0) 0) |
| [15] |
Tapken U, Enghardt L. Optimization of Sensor Arrays for Radial Mode Analysis in Flow Ducts[R]. AIAA 2006-2638. http://www.researchgate.net/publication/224985606_Optimisation_of_sensor_arrays_for_radial_mode_analysis_in_flow_ducts
(  0) 0) |
| [16] |
Enghardt L, Tapken U, Neise W, et al. Active Control of Fan Noise from High-Bypass Aeroengines: Experimental Results[J]. The Aeronautical Journal of the Royal Aeronautical Society, 2002, 106(3).
(  0) 0) |
| [17] |
Enghardt L, Tapken U, Kornow O, et al. Acoustic Mode Decomposition of Compressor Noise under Consideration of Radial Flow Profiles[R]. AIAA 2005-2833. https://www.researchgate.net/publication/224797831_Acoustic_Mode_Decomposition_of_Compressor_Noise_under_Consideration_of_Radial_Flow_Profiles
(  0) 0) |
| [18] |
Enghardt L, Tapken U, Neise W, et al. Turbine Blade/ Vane Interaction Noise: Acoustic Mode Analysis Using In-duct Sensor Rakes[R]. AIAA 2001-2153. http://arc.aiaa.org/doi/abs/10.2514/6.2001-2153
(  0) 0) |
| [19] |
Tapken U, Bauers R, Neuhaus L, et al. A New Modular Fan Rig Noise Test and Radial Mode Detection Capability[R]. AIAA 2011-2897. https://arc.aiaa.org/doi/abs/10.2514/6.2011-2897
(  0) 0) |
| [20] |
Dahl M D, Hixon R, Sutliff D L. Further Development of Rotating Rake Mode Measurement Data Analysis[R]. AIAA 2013-2246. http://arc.aiaa.org/doi/abs/10.2514/6.2013-2246?mi=8ebqhb&af=R&contents=articlesChapters&countTerms=true&field1=Contrib&target=default&text1=Dahl%2C+Milo
(  0) 0) |
| [21] |
Taddei F, Lucia M D, Torzo D, et al. A Comparison Between Radial Rakes of Sensors and Axial Arrays of Microphones for the Experimental Investigation of Tone Noise in LPTs[R]. AIAA 2013-2245. http://arc.aiaa.org/doi/abs/10.2514/6.2013-2245
(  0) 0) |
| [22] |
Spitalny M, Tapken U. Radial Mode Analysis of Ducted Sound Fields with Sensor Rakes and Wall Flush Sensor Arrays under Consideration of a Radial Flow Profile[R]. AIAA 2016-3037. http://www.researchgate.net/publication/303601964_Radial_Mode_Analysis_of_Ducted_Sound_Fields_with_Sensor_Rakes_and_Wall_Flush_Sensor_Arrays_under_Consideration_of_a_Radial_Flow_Profile
(  0) 0) |
| [23] |
Nelson P A, Yoon S H. Estimation of Acoustic Source Strength by Inverse Methods: Part Ⅰ, Conditioning of the Inverse Problem[J]. Journal of Sound and Vibration, 2000, 233(4): 639-664. DOI:10.1006/jsvi.1999.2837
(  0) 0) |
| [24] |
Kim Y, Nelson P A. Estimation of Acoustic Source Strength within a Cylindrical Duct by Inverse Methods[J]. Journal of Sound and Vibration, 2004, 275(1): 391-41.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

