2. 中国空气动力研究与发展中心 高超中心,四川 绵阳 621000
2. Air-breathing Hypersonic Technology Research Center, China Aerodynamics Research and Development Center, Mianyang 621000, China
飞行器模型在脉冲燃烧风洞中进行测力试验时,风洞启动产生的高速气流会对测力系统产生一个瞬态冲击,从而使系统产生瞬态振动,由于脉冲风洞试验时间短[1~3],仅有100~300ms,在试验过程中振动不能衰减完全,从而影响测力试验数据的准确性。此外,模型振动严重时还会危及试验设备和人员的安全,缩短设备的使用寿命,造成系统故障率上升[4]。
国内外对风洞测力系统减振技术开展了大量研究[4~14]。梁鉴等[4]利用增加阻尼以降低振动的方法并且在不改变风洞现有结构的前提下设计了一套抑振装置,该装置工作后有效的抑制了模型的纵向振动,振动幅值降低了一个量级。Igoe W B等[5]通过在飞行器模型内安装被动式阻尼器来抑制模型的振动,取得了一定的效果。佘重禧等[6]建立了飞行器模型降阶后的有限元模型,并基于一种简化的H混合灵敏度控制方法,实现了模型低频大幅俯仰振动的主动抑制,并采用仿真的方式验证了模型振动抑制的效果。王学等[7]在飞行器模型内部安装压电陶瓷堆作动器,通过作动器产生的激励力来降低飞行器模型的振动强度,其中控制系统利用天平实时测力数据作为反馈信号,该研究还对比了压电陶瓷安装在不同位置时的抑振效果。刘巍等[8]提出了一种基于叠堆式压电陶瓷作动器的模型主动抑振策略。通过实时测试飞行器模型的振动,基于PD调节器的控制系统依据此信号输出控制信号给抑振器。地面试验表明,抑振器具有提高支杆系统阻尼的能力,对风洞模型在俯仰和偏航两个方向上的抑振效果明显。陈卫东等[9]采用主动控制原理设计了一套模型抑振装置。将电磁式作动器装载于试验模型的内部空腔,基于学习控制算法对测力系统的振动进行实时的控制,并通过地面试验验证了抑振装置的有效性。S.Balakrishna[10~12]等在飞行器模型内安装压电陶瓷作动器并与测力天平构成闭环控制系统,天平信号为控制系统提供反馈信号,控制系统向压电陶瓷作动器发送控制信号,压电陶瓷作动器产生激振力,从而使得飞行器模型的振动得到衰减。Pereira[13]等设计了一套阻尼系统并安装在飞行器模型内,该阻尼系统通过压电作动器来对飞行器模型的振动进行抑制,并通过实验验证了该阻尼系统的有效性。Shuai Li[14]等选择对支架进行优化来改善测力系统整机动态特性,从而达到降低测力系统振动强度的效果。
通过对已有文献分析发现,目前对风洞测力系统抑振措施的研究主要集中于振动的主动或被动控制,通过动态特性优化来改善测力系统动态特性的研究较少,在较少的此类研究中,动态特性优化又主要集中于对零部件的优化,而对结合部进行优化的方法尚未见报道。本文提出了一种通过结合部优化来改善测力系统整机动态特性从而降低系统振动强度的方法。首先,基于Ansys建立了测力系统整机动力学模型,其中采用弹簧-阻尼模型来描述结合部的动态特性,并根据Yoshimura法计算出弹簧-阻尼单元的刚度系数和阻尼系数。在准确建立整机有限元模型的基础上,对其进行理论模态分析,计算测力系统中各零部件和结合部在各阶模态下的应变能密度分布,通过对比零部件和结合部的应变能密度大小来揭示结合部动态特性对测力系统整机动态特性的影响程度,最后通过结合部动态特性优化来实现测力系统整机动态特性的提升。
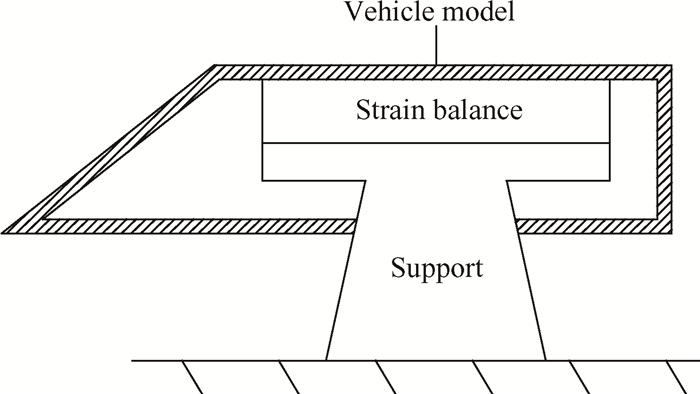
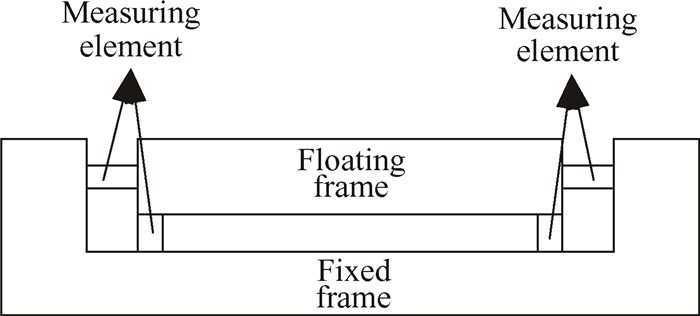
2 测力系统概述本文的研究对象为某脉冲燃烧风洞测力系统。该测力系统的结构简图如图 1所示,主要由飞行器模型,天平和支架组成。天平、飞行器模型与支架间均采用16个M16的螺钉进行连接。其中测力天平为盒式应变天平,其结构简图如图 2所示,由浮动框、固定框和弹性测量元件组成,弹性测量元件将浮动框和固定框连接成一整体。工作时风洞产生的气流作用在飞行器模型上产生气动力,使得天平浮动框与固定框发生相对位移,粘贴于测量元件上的箔式应变计产生形变,从而导致电阻发生变化,惠斯通电桥将电阻的变化转变为电压输出,此即测力系统的测试原理。
|
Fig. 1 Diagram of force measuring system |
|
Fig. 2 Instruction diagram of strain balance |
脉冲燃烧风洞测力试验过程中,风洞启动产生的高速气流会对测力系统产生瞬态冲击从而诱发测力系统发生瞬态振动,由于测试时间短,在有效试验时间内振动不能衰减完全,此时天平测量元件处的位移x(t)为瞬态振动所引起的位移x1(t)与气动力作用下所产生的位移x2(t)的综合x(t)= x1(t)+ x2(t),根据应变天平测试原理F(t)= K·x(t),其中F(t)为辨识出的气动力,x(t)为天平元件在试验过程中的位移,K为常数,通过天平静态标定试验获得。由此可知,测力系统的瞬态振动会对天平测试精度产生不可忽视的影响,振动强度越大,误差越大。
根据模态理论的相关知识,测力系统各点的振动响应由激励力频率范围内的模态数与模态振型共同决定,改善测力系统动态特性(包括:提高各阶模态固有频率与降低频响特性曲线在各阶模态处的幅值)有助于降低天平测量元件处的振动响应,从而达到提高测力系统测试精度的目的。
4 基于结合部优化的整机动态性能优化结合部指的是零部件间相互接触并传递位移与载荷的部位。机床动力学领域的大量研究表明[15],结合部动态特性对整机动态特性有着重要影响,对于风洞测力系统而言,从本质上看,其与机床一样,均为组合体,因此测力系统中的结合部动态特性对系统整机动态特性理应存在重要影响,通过结合部的优化能够有效改善测力系统整机动态特性。然而,目前关于测力系统结合部动态特性对整机动态特性影响的研究尚未见报道,因此本文首先基于Ansys研究了测力系统中结合部动态特性对整机动态特性的影响。
4.1 脉冲风洞测力系统有限元建模 4.1.1 测力系统几何模型的简化测力系统中包含许多微小结构,例如孔,倒角和圆角等,它们对整机动态特性影响很小,但在有限元分析中会明显增加网格数量,增大计算量,因此,对整机模型进行合理的简化能有效降低计算成本,提高计算效率。本研究按照以下原则对测力系统进行简化:
(1) 忽略结构中的小倒角和圆角。
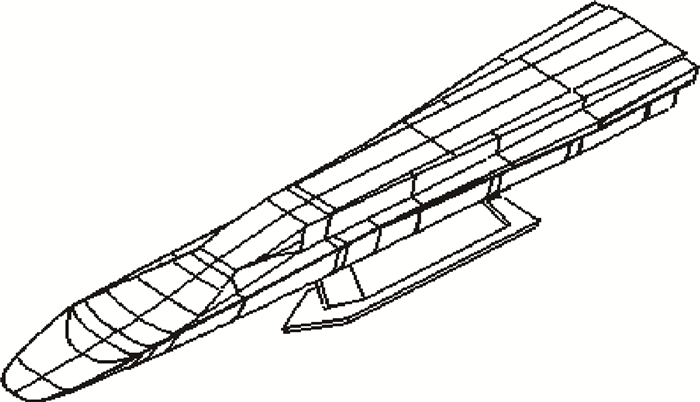
(2) 删除结构中的小定位孔及螺纹孔等细小特征。简化后的模型如图 3所示。
|
Fig. 3 Simplified model of force measuring system |
测力系统是由各零部件通过结合部连接而成的,因此测力系统的动力学建模包括单一零部件的建模和结合部的建模。
4.1.2.1 单一零部件建模测力系统的主要零部件有飞行器模型,应变天平和支架。飞行器模型选用不锈钢加工,天平材料为00Ni18Co8Mo5TiAl,模型支架为碳钢,上述材料的主要参数如表 1所示。在Ansys中采用20节点的Solid186单元和10节点的Solid187单元分别对飞行器模型,天平和支架进行网格划分。共得到88455个单元,181626个节点。
|
|
Table 1 Material Properties |
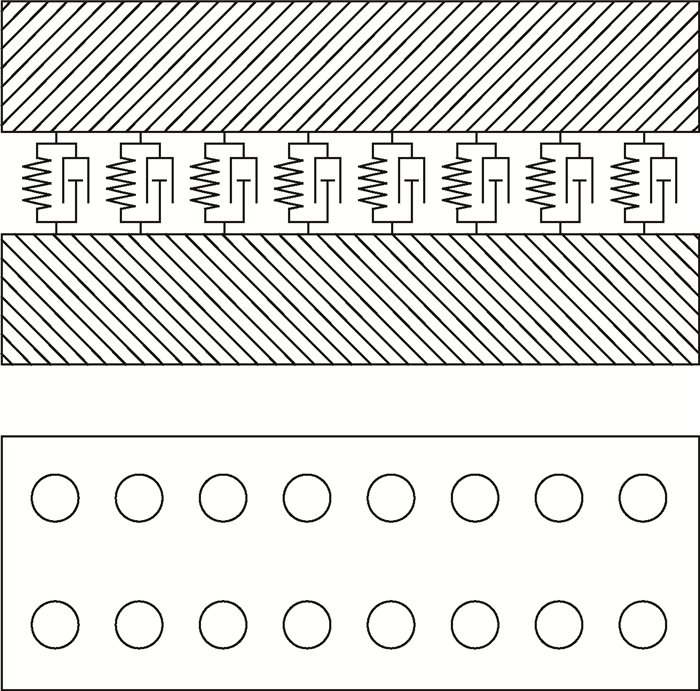
研究表明,结合部的阻尼,刚度分别占整体阻尼与刚度的90%和60%以上[15],因此在测力系统动力学建模时必须正确描述结合部的动态特性。在测力系统中对整机动态特性起主要作用的结合部为飞行器模型-天平螺钉固定结合部,天平-支架螺钉固定结合部。由于结合部表现出即存储能量又释放能量的特点[16],因此本文采用弹簧-阻尼模型来描述测力系统中主要结合部的动态特性,对系统动态特性影响较小的结合部在Ansys中采用粘接处理。在结合部中每一个螺钉位置用一个法向弹簧阻尼单元和两个切向弹簧阻尼单元描述,结合部的弹簧-阻尼模型如图 4所示,其中圆圈代表螺钉的位置。
|
Fig. 4 Spring damping model of joint part |
弹簧阻尼单元中的刚度和阻尼系数采用理论计算的方法获得,计算流程为:首先根据Yoshimura法获得结合面单位面积的刚度系数和阻尼系数;其次,对结合面上单位面积的刚度系数和阻尼系数求积分得到结合部整体刚度系数和阻尼系数;最后,将其均分给所有弹簧-阻尼单元,就得到了每个弹簧-阻尼单元中的刚度系数和阻尼系数。结合部整体刚度系数和阻尼系数计算公式[17]如下:
| $ {{\mathit{K}}_{\rm{n}}}\rm{=}\int{{{\mathit{k}}_{\rm{n}}}\rm{(}{{\mathit{p}}_{\rm{n}}}\rm{)d}\mathit{s}} $ | (1) |
| $ {{\mathit{K}}_{\rm{t}}}\rm{=}\int{{{\mathit{k}}_{\rm{t}}}\rm{(}{{\mathit{p}}_{\rm{n}}}\rm{)d}\mathit{s}} $ | (2) |
| $ {{\mathit{C}}_{\rm{n}}}\rm{=}\int{{{\mathit{c}}_{\rm{n}}}\rm{(}{{\mathit{p}}_{\rm{n}}}\rm{)d}\mathit{s}} $ | (3) |
| $ {{\mathit{C}}_{\rm{t}}}\rm{=}\int{{{\mathit{c}}_{\rm{t}}}\rm{(}{{\mathit{p}}_{\rm{n}}}\rm{)d}\mathit{s}} $ | (4) |
式中Kn,Kt,Cn,Ct分别为某一结合部的法向总刚度、法向总阻尼系数,切向总刚度、切向总阻尼系数;pn为结合部面压;kn(pn),cn(pn),kt(pn),ct(pn)为某一结合面上单位接触面积的法向刚度、阻尼系数和单位接触面积的切向刚度、阻尼系数。
其中结合部面压可由计算公式(5),(6)获得
| $ {{\mathit{p}}_{\rm{n}}}\rm{=}\frac{\rm{2}\mathit{T}}{\rm{tan(}\mathit{\varphi }\rm{+}{{\mathit{\rho }}_{\mathit{V}}}\rm{)}{{\mathit{d}}_{\rm{2}}}\rm{+2}\mathit{\mu r}} $ | (5) |
| $ \mathit{r}\rm{=}\frac{\mathit{D}_{\rm{W}}^{3}\rm{-}\mathit{d}_{0}^{3}}{\rm{3(}\mathit{D}_{\rm{W}}^{2}\rm{-}\mathit{d}_{0}^{2}\rm{)}} $ | (6) |
式中d2为螺纹中径;φ为螺纹升角;ρV为螺纹当量摩擦角;μ为螺母与被连接件支撑面间的摩擦因数;DW为六角螺母直径;d0为螺钉中径;T为螺钉的预紧力矩。
由公式(5),(6)计算出结合面面压,通过查询文献[18]可以得到结合面单位接触面积的刚度与阻尼系数,由公式(1)~(4)求出结合部总刚度系数和总阻尼系数。以飞行器模型-天平螺钉固定结合部,天平-支架螺钉固定结合部为例,根据设计要求计算出飞行器模型-天平螺钉固定结合部与天平-支架螺钉固定结合部的结合面面压分别为8.95MPa,2.4MPa,结合部中各结合面的粗糙度均为3.2 μm,基于结合面压查询文献[18]得到的单位接触面积的刚度与阻尼系数分别如表 2所示,计算得到的单个弹簧阻尼单元的刚度系数和阻尼系数如表 3所示。
|
|
Table 2 Basic parameters of the joint part/(k/(N/m3); c/(N·s/m3)) |
|
|
Table 3 Stiffness coefficient and damping coefficient of spring-damp element/(K/(N/m); C/(N/(m·s))) |
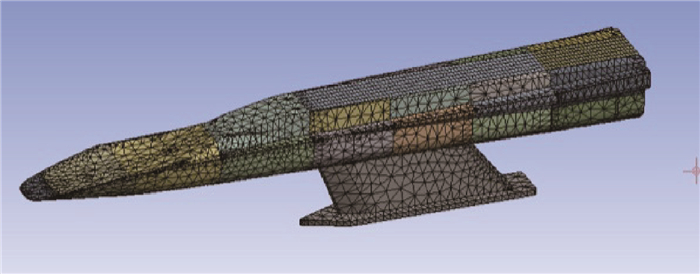
综合所有单一整体零部件的有限元模型与结合部的弹簧阻尼模型,得到测力系统整机动力学模型如图 5所示。其中支架与地面的连接采用完全固定的约束方式。
|
Fig. 5 Finite element model of force measuring system |
本文通过对比零部件与结合部在各阶模态下的应变能密度大小,揭示结合部的动态特性对整机动态特性的影响。结构在外力作用下产生弹性变形时,在结构内部将积蓄应变能,每单位体积物体内所积蓄的应变能称为应变能密度,计算公式为
| $ \mathit{E}_{\mathit{s}}^{\mathit{r}}\rm{=}\frac{{{\rm{(}\mathit{A}_{\mathit{s}}^{\mathit{r}}\rm{)}}^{\rm{T}}}{{\mathit{\boldsymbol{K}}}_{\mathit{s}}}\rm{(}\mathit{A}_{\mathit{s}}^{\mathit{r}}\rm{)}}{{{\mathit{V}}_{\mathit{s}}}} $ | (7) |
式中Esr为结构S在r阶模态下的应变能密度;Asr为结构S中所有自由度在r阶模态下的振型;(Asr)T为Asr的转置向量;Ks为结构S的刚度矩阵;Vs为结构S的体积;
由应变能密度可以直观的看出测力系统在各阶模态下振动时的应变能分布,若某个由N个零部件组成的系统,其中第S个结构的应变能密度均高于其它零部件的应变能密度,表明该零部件为整机刚度最为薄弱处,因此优化该结构的刚度比优化其它结构的刚度能更为有效地改善系统的动态特性,由此说明它对整机动态特性存在重要影响。
4.2.1 整机动态特性影响因素对比不同的飞行器模型、天平与支架组成了不同的测力系统,由此可知,不同测力系统中结合部动态特性对整机动态特性的影响程度也不相同,为了揭示在普遍情况下结合部动态特性对测力系统整机动态特性的影响,笔者分别研究了在飞行器模型、天平与支架动态特性发生改变的前提下,结合部动态特性对整机动态特性的影响程度。零部件的动态特性是由其刚度分布、质量分布和阻尼分布决定的,研究表明[15],组合体90%以上的阻尼来源于结合部,零部件自身的结构阻尼相比于结合部处的阻尼可以忽略不计,因此本研究不考虑零部件的结构阻尼。不同的测力系统其零部件的动态特性均不同,可以通过在不改变零部件形状的条件下改变其弹性模量、密度来模拟不同测力系统中零部件动态特性的变化。综上所述,笔者采用对测力系统中结合部应变能密度和零部件应变能密度进行比较的方法,分别研究了飞行器模型、天平与支架的弹性模量和密度变化情况下,结合部对测力系统整机动态特性的影响程度。
分别改变飞行器模型、天平与支架的弹性模量和密度,并且每次只改变一个零部件中的某一个参数,总共得到23种分析方案,采用Ansys有限元分析软件对所有方案的前五阶模态进行分析,根据公式(7)计算测力系统在各阶模态下所有零部件的平均应变能密度和结合部的应变能密度,如表 4~9所示。通过观察发现,随着飞行器模型弹性模量的增大,零部件和结合部处的应变能密度在任意模态下均不断增大,并且在任意方案中,结合部的应变能密度要大于零部件,只有第四阶模态下结合部处的应变能密度要小于零部件。当改变飞行器模型的密度时,如表 5所示,随着飞行器模型密度的增大,零部件和结合部处的应变能密度在任意模态下不断减小,并且在任意方案中,结合部的应变能密度要大于零部件,只有第四阶模态下结合部处的应变能密度要小于零部件。通过上述分析可以说明,对于不同的飞行器模型所组成的测力系统,结合部均为整机刚度最为薄弱的地方,使得整机出现低频振动,并且增大了测力系统振动的幅度。如表 6-9所示,当分别改变天平与支架的弹性模量和密度时,系统应变能密度分布展现出了与表 4-5相同的规律性。通过观察发现在任意方案中,结合部的应变能密度均要大于结合部处的应变能密度,只有第四阶模态下结合部处的应变能密度要小于零部件。综上所述,在大多数的风洞测力系统中,结合部均为整机中刚度最为薄弱的地方,因此,通过改善结合部动态特性相较于其它零部件而言能更为有效地提升测力系统整机动态特性,然而现有的研究只是对单一零部件的动态特性进行改善以此来提高整机的动态特性。
|
|
Table 4 Strain energy density distribution of force-measuring system after modifying aircraft elasticity modulus |
|
|
Table 5 Strain energy density distribution of force-measuring system after modifying aircraft density |
|
|
Table 6 Strain energy density distribution of force-measuring system after modifying strain balance elasticity modulus |
|
|
Table 7 Strain energy density distribution of force-measuring system after modifying strain balance density |
|
|
Table 8 Strain energy density distribution of force-measuring system after modifying support elasticity modulus |
|
|
Table 9 Strain energy density distribution of force-measuring system after modifying support density |
根据上节研究得到的结论,以应变能密度最大的结合部作为整机动态特性优化的部位。由Yoshimura法可知,结合部的刚度与接触面面压、粗糙度、材料及面积有关,由于设计要求的限制,结合面粗糙度、材料及面积只能在很小的范围内进行优化,效果有限,因此本文选用接触面面压作为优化变量来改善结合部的刚度,从而达到优化测力系统整机动态特性的目的,其中结合部的面压可以通过调整螺钉的预紧力矩来实现。本研究以结合部的接触面压为优化变量列出表 10所示的9组优化方案。采用Yoshimura法计算每组方案下的弹簧-阻尼单元刚度系数和阻尼系数并将其带入到Ansys中进行计算,分析发现,第9组优化方案下的结合部应变能密度改善最为明显,因此选用第9组方案为结合部最终优选方案。
|
|
Table 10 Optimization scheme of joint |
对优化前后的测力系统有限元模型进行模态分析,表 11列出了优化前后整机前五阶模态的比较结果,从表中可以看出优化后的测力系统各阶固有频率比优化前均有较明显提高。
|
|
Table 11 Comparison between each order natural frequency of force-measuring system before and after optimization |
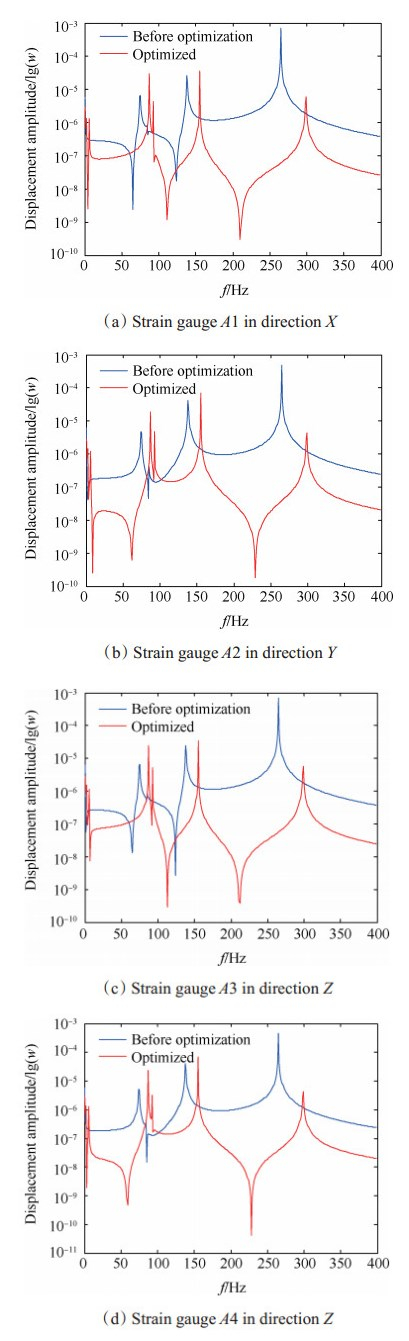
分别对优化前后的测力系统整机模型进行谐响应分析,提取应变天平中应变片粘贴处的频响函数,它是反映测力系统整机振动强度的重要指标,应变片在天平中的所在位置A1, A2, A3, A4如图 6所示。由于测力系统所测得力指的是飞行器模型重心处的集中力,这是因为做飞行器飞行动力学分析时需要将其看成是刚体,并将面力形式的气动力等效成作用在飞行器重心处的集中力。风洞测力试验的目的是给出飞行器模型在各种飞行条件下其重心处所受的集中力,基于此在设计时给予了飞行器模型较高的刚度,尽量让其传力特性接近于刚体的传力特性,所以,可以将飞行器模型近似成一个刚体,因此在飞行器模型重心处的XYZ方向依次施加0~400Hz的正弦扫频激励力。通过计算,飞行器模型重心在笛卡尔坐标系中的位置如表 12所示。由于飞行器模型的重心并不在飞行器上,因此将重心沿X,Y,Z方向投影至飞行器模型上,如图 7中的A,B,C三点。分别在此三点处施加幅值为1kN,激振频率为0~400Hz的简谐力,其中A点施加X方向的激振力,B点施加Y方向的激振力,C点施加Z方向上的激振力,对测力系统进行整机谐响应分析,并提取天平中各应变片粘贴位置的位移幅频特性曲线,对比优化前后天平中各应变片的位移幅频特性曲线如图 8所示,由于篇幅限制,本文只选取了A1处X方向、A2处Y方向、A3处Z方向与及A4处Z方向的位移幅频特性曲线作为展示。在图 8(a),(d)中w分别表示应变计粘贴处A1~A4沿各自的激振力方向做简谐振动时的幅值,单位为m。

|
Fig. 6 Paste position of foil strain gauge |
|
|
Table 12 Barycentric coordinate of vehicle model |

|
Fig. 7 Projection of exciting force point |
|
Fig. 8 Displacement amplitude frequency characteristic curve of strain gauge A1, A2, A3, A4 comparison between force-measuring system before and after optimization |
通过对图 8的观察发现,优化后天平所有应变片A1,A2,A3,A4处的位移幅频特性曲线的幅值要比优化前有明显的降低。采用优化前后A1,A2,A3,A4处的位移幅频特性曲线与横坐标轴(频率)所围成面积的改变量来描述位移幅频特性曲线的综合改变程度,计算公式如(8)所示。其中S1,S2分别表示优化前后位移幅频特性曲线与横坐标轴(频率)所围成的面积,Δ表示优化前后测力系统中A1,A2,A3,A4处位移幅频特性曲线的综合改变程度。基于公式(8)计算出A1,A2,A3,A4在X,Y,Z方向的位移幅频特性曲线综合改变程度如表 13所示,从中分析发现,A1,A2,A3,A4处沿X,Y,Z方向优化后的位移幅频特性曲线幅值比优化前均降低了15%以上,由此可以说明,优化后测力系统整机动态性能较优化前得到明显的改善。
| $ \mathit{\Delta }\rm{=}\frac{{{\mathit{S}}_{\rm{1}}}\rm{-}{{\mathit{S}}_{\rm{2}}}}{{{\mathit{S}}_{\rm{1}}}}\times \rm{100 }\% $ | (8) |
|
|
Table 13 Degree of amplitude-frequency response curve change between force-measuring system before and after optimization(%) |
从表 11可以看出,结合部优化后各阶模态频率比优化前都有明显的增大,其中第一阶模态频率提高达到16.7%。
5 结论通过对结果分析,可以得出以下结论:
(1) 测力系统整机应变能密度分布分析发现:结合部处的应变能密度要远大于其余零部件,而应变能密度越大代表该处刚度越薄弱,说明对结合部进行动态特性优化能有效地改善整机动态特性,同时也说明结合部的动态特性对整机的动态特性有重要的影响。
(2) 以飞行器模型-天平,天平-支架结合部中的接触面压为优化变量对测力系统进行动态特性优化,对比优化前后测力系统前五阶固有频率可以发现:优化后测力系统各阶固有频率相较于优化前有明显的提高,最高提高了16.7%。对优化前后的测力系统进行了谐响应分析,提取天平中应变片粘贴处的位移幅频特性曲线并进行对比,发现优化后所有应变片粘贴处的位移幅频特性曲线幅值相较于优化前均有明显的降低,均降低了15%以上,由此说明测力系统整机动态特性得到了较好的改善,从而验证了所提出的基于结合部优化的整机动态特性优化方法的可行性与有效性。
| [1] |
乐嘉陵. 吸气式高超声速技术研究进展[J]. 推进技术, 2010, 31(6): 641-649. (LE Jia-ling. Progress in Air-Breathing Hypersonic Technology[J]. Journal of Propulsion Technology, 2010, 31(6): 641-649.)
(  0) 0) |
| [2] |
刘伟雄, 谭宇, 毛雄兵, 等. 一种新运行方式脉冲燃烧风洞研制及初步应用[J]. 实验流体力学, 2007, 21(4): 59-64. (  0) 0) |
| [3] |
王振锋, 白菡尘, 李向东. 脉冲燃烧风洞点式油流技术在压缩拐角流动显示中的应用[J]. 推进技术, 2014, 35(11): 1455-1460. (WANG Zhen-feng, BAI Han-chen, LI Xiang-dong. Application of Oil Flow Visualization Technique in a Pulse Type High Temperature Wind Tunnel to Visualize Compression Corner Flow[J]. Journal of Propulsion Technology, 2014, 35(11): 1455-1460.)
(  0) 0) |
| [4] |
梁鉴, 张卫国, 王勋年, 等. 4m×3m风洞无人机模型振动抑制系统研制[J]. 实验流体力学, 2007, 21(4): 65-70. (  0) 0) |
| [5] |
Capone F J, Igoe W B. Reduction of Wind-TunnelModel Vibration by Means of a Tuned Damped Vibration Absorber Installed in the Model[R]. NASA TM-1968.
(  0) 0) |
| [6] |
佘重禧, 陈卫东, 邵敏强. 跨声速风洞测力模型的降阶及[H∞]减振控制[J]. 噪声与振动控制, 2014, 34(1): 67-71. (  0) 0) |
| [7] |
王学, 陈陆军, 黄勇, 等. 低速风洞模型振动主动控制仿真研究[J]. 振动与冲击, 2014, 33(5): 14-19. (  0) 0) |
| [8] |
刘巍, 毕晓丹, 贾振元, 等. 风洞模型主动抑振器的设计与实验[J]. 光学精密工程, 2015, 23(10): 2895-2901. (  0) 0) |
| [9] |
陈卫东, 邵敏强, 杨兴华, 等. 跨声速风洞测力模型主动减振系统的试验研究[J]. 振动工程学报, 2007, 20(1): 91-96. (  0) 0) |
| [10] |
Balakrishna S, Houlden H, Butler D, et al. Development of a Wind Tunnel Active Vibration Reduction System[C]. Reno: 45th AIAA Aerospace Sciences Meeting and Exhibit, 2007.
(  0) 0) |
| [11] |
Balakrishna S, Butler D, White E, et al. Active Damping of Sting Vibrations in Transonic Wind Tunnel Testing [C]. Reno: 46th AIAA Aerospace Sciences Meeting and Exhibit, 2008.
(  0) 0) |
| [12] |
Rivers M B, Balakrishna S. NASA Common Research Model Test Envelope Extension with Active Sting Damping at NTF[C]. Atlanta: 32nd AIAA Applied Aerodynam ics Conference, 2014.
(  0) 0) |
| [13] |
Pereira J L. Development of an Active Damping System for Use with a Single Strut Mount[C]. San Diego: 54th AIAA Aerospace Sciences Meeting, 2016.
(  0) 0) |
| [14] |
Li S, Liu D, Li Q. The Optimal Design of a Wind Tunnel Model Sting System Based on the CFD Method[J]. International Journal of Heat & Technology, 2015, 33(4): 137-144.
(  0) 0) |
| [15] |
Zhang G P, Huang Y M, Shi W H, et al. Predicting Dynamic Behaviours of a Whole Machine Tool Structure Based on Computer-Aided Engineering[J]. International Journal of Machine Tools and Manufacture, 2003, 43(7): 699-706. DOI:10.1016/S0890-6955(03)00026-9
(  0) 0) |
| [16] |
邓聪颖, 殷国富, 肖红. 基于能量分布的机床整机动态特性优化方法[J]. 振动、测试与诊断, 2015, 35(6): 1083-1089. (  0) 0) |
| [17] |
廖伯瑜, 周新民, 尹志宏. 现代机械动力学及其工程应用:建模, 分析, 仿真, 修改, 控制, 优化[M]. 北京: 机械工业出版社, 2004.
(  0) 0) |
| [18] |
学良. 机械结合面动态特性及应用[M]. 北京: 中国科学技术出版社, 2002.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

