航空发动机轮盘经常受到具有平均应力或平均应变的非对称循环载荷。现有很多研究[1~5]表明,平均应力和平均应变对疲劳寿命有明显的影响。从裂纹扩展的角度来看,正平均应力使裂纹张开并促进裂纹扩展,而负平均应力使裂纹闭合并阻碍裂纹扩展,且在长寿命区平均应力影响较大,而在短寿命区影响较小[6]。平均应变的出现则相当于对构件施加了预应变,会在某些情况下消耗材料的一部分有效延性,缩短其疲劳寿命。已有试验结果表明,非弹性的预应变会对疲劳寿命产生明显的影响[7]。对于这种由于平均应变的出现而使结构产生显著损伤的现象,研究人员提出了多种解释[8]:一种解释是大的预应变可以形成微小裂纹,而这种裂纹在后续的载荷作用下进行扩展;还有一种解释是材料的这些非弹性预应变使屈服点消失并引起软化,然后由于循环塑性应变的增大而使材料损伤加快。
涡轮盘常经受较大载荷,部分危险点明显进入屈服,需要采用应变寿命模型[9, 10]进行疲劳寿命预估。对于平均应力和平均应变对低周疲劳寿命的影响,已有很多学者都提出了相应的疲劳寿命模型。Morrow认为平均应力对由弹性应变主控的长寿命区有明显的影响,而对于由塑性应变主控的短寿命区则因应力松弛等原因影响较小,可忽略不计,从而提出了Morrow弹性修正模型[11]。可以预测,由于Morrow弹性修正模型的假设条件导致其在计算低周疲劳时精度不高。Manson和Halford提出弹性分量与塑性分量均应被修正以充分考虑平均应力效应的M-H修正模型[12],但在使用中发现该模型在塑性应变主控的短寿命区预测结果偏危险[13]。Smith等提出了SWT平均应力修正模型[3],该模型采用σmaxεa作为损伤参量,认为只要σmaxεa相同,不同组合的σmax和εa对应于相同的Nf。SWT模型从能量的角度考虑了平均应力对疲劳寿命的影响,对灰铸铁、碳素钢、低合金钢等预测效果较好[14, 15],但在短寿命区预测结果偏保守[16]。Dowling将Walker模型与Manson-Coffin公式结合,提出了一种考虑平均应力影响的应变寿命模型[17],但该模型需首先由应力疲劳试验数据拟合得到平均应力影响敏感度参数γ,然后再采用应变疲劳试验数据拟合模型其余待定参数,对试验数据要求较高,且过程较为繁琐。
为了更准确地描述平均应变对疲劳寿命的影响,本文基于Manson-Coffin公式提出了一个考虑应变比(或平均应变)影响的应变寿命新模型。该模型不仅考虑了应变比对疲劳寿命的影响,同时也考虑了应变比对疲劳寿命的影响随寿命的改变而变化的现象。对至少具有两种不同应变比下的疲劳试验数据采用多元线性回归分别拟合弹性分量和塑性分量的相关参数,该模型可计算试验数据应变比覆盖范围内任意应变比下的疲劳寿命。为了验证、对比该模型的精度,分别采用CC450不锈钢、SAE1045钢以及GH4133合金的光滑试棒和中心孔拉伸试件的疲劳试验结果与四种考虑平均应力和平均应变影响的疲劳寿命模型的计算结果作对比,并进行了分析说明。
2 常用考虑平均应力影响的应变寿命模型众所周知,Manson-Coffin公式中的参数由应变比R=-1时的疲劳试验数据拟合得到,从而适用于计算εm = 0时的疲劳寿命。然而,当构件经受非对称载荷从而在危险部位存在平均应变时,便不能再直接使用Manson-Coffin公式,需要进行一定的修正。目前工程中常用的考虑平均应力修正的应变寿命模型有:Morrow弹性修正模型、Manson-Halford修正模型(后简称M-H模型)、SWT修正模型以及Walker修正模型[17]。
Morrow弹性修正模型是在Manson-Coffin公式的基础上对弹性部分进行了平均应力修正,如式(1)所示。M-H修正模型则对弹性分量和塑性分量均进行了修正,如式(2)所示。SWT模型由Basquin公式与Manson-Coffin公式得到,如式(3)所示。Walker应变寿命模型将Walker应力寿命公式与Manson-Coffin公式相结合,如式(4)所示,其中γ为与材料相关的待定参量,需要通过不同应力比下的应力疲劳数据拟合得到,式中R为应力比。
| $ {\mathit{\varepsilon }_{\rm{a}}}{\rm{ = }}\frac{{{{\mathit{\sigma '}}_{\rm{f}}}{\rm{ - }}{\mathit{\sigma }_{\rm{m}}}}}{\mathit{E}}{{\rm{(2}}{\mathit{N}_{\rm{f}}}{\rm{)}}^\mathit{b}}{\rm{ + }}{{\mathit{\varepsilon '}}_{\rm{f}}}{{\rm{(2}}{\mathit{N}_{\rm{f}}}{\rm{)}}^\mathit{c}} $ | (1) |
| $ {{\mathit{\varepsilon }}_{\rm{a}}}\rm{=}\frac{{{{\mathit{{\sigma }'}}}_{\rm{f}}}\rm{-}{{\mathit{\sigma }}_{\rm{m}}}}{\mathit{E}}{{\rm{(2}{{\mathit{N}}_{\rm{f}}}\rm{)}}^{\mathit{b}}}\rm{+}{{{\mathit{{\varepsilon }'}}}_{\rm{f}}}{{\left( \frac{{{{\mathit{{\sigma }'}}}_{\rm{f}}}\rm{-}{{\mathit{\sigma }}_{\rm{m}}}}{{{{\mathit{{\sigma }'}}}_{\rm{f}}}} \right)}^{{}^{\mathit{c}}\!\!\diagup\!\!{}_{\mathit{b}}\;}}{{\rm{(2}{{\mathit{N}}_{\rm{f}}}\rm{)}}^{\mathit{c}}} $ | (2) |
| $ {\mathit{\sigma }_{{\rm{max}}}}{\mathit{\varepsilon }_{\rm{a}}}{\rm{ = }}\frac{{\mathit{\sigma '}_{\rm{f}}^2}}{\mathit{E}}{{\rm{(2}}{\mathit{N}_{\rm{f}}}{\rm{)}}^{{\rm{2}}\mathit{b}}}{\rm{ + }}{{\mathit{\sigma '}}_{\rm{f}}}{{\mathit{\varepsilon '}}_{\rm{f}}}{{\rm{(2}}{\mathit{N}_{\rm{f}}}{\rm{)}}^{\mathit{b}{\rm{ + }}\mathit{c}}} $ | (3) |
| $ {\mathit{\varepsilon }_{\rm{a}}}{\rm{ = }}\frac{{{{\mathit{\sigma '}}_{\rm{f}}}}}{\mathit{E}}{\left( {\frac{{1 - \mathit{R}}}{2}} \right)^{{\rm{1 - }}\mathit{\gamma }}}{{\rm{(2}}{\mathit{N}_{\rm{f}}}{\rm{)}}^\mathit{b}}{\rm{ + }}{{\mathit{\varepsilon '}}_{\rm{f}}}{\left( {\frac{{1 - \mathit{R}}}{2}} \right)^{\mathit{c}{\rm{(1 - }}\mathit{\gamma }{\rm{)}}/\mathit{b}}}{{\rm{(2}}{\mathit{N}_{\rm{f}}}{\rm{)}}^\mathit{c}} $ | (4) |
尽管第2节中列举了多位学者所提出的考虑平均应力影响的应变寿命模型,但在使用中发现这些模型在部分情况下疲劳寿命的预测精度难以满足工程需求,均存在一定的局限性。同时,通过对疲劳试验数据研究发现,在长寿命区时平均应力和平均应变对疲劳寿命影响较大,而在短寿命区影响则相对较小[10],也就是说平均应力和平均应变对疲劳寿命的影响随着寿命的减小而降低。然而上述模型均未能反映该现象。
Manson-Coffin公式是最常用的计算低周疲劳的应变寿命模型。本文在Manson-Coffin公式的基础上分别拟合弹性分量和塑性分量与疲劳寿命的关系时,均添加了应变比项和应变比与疲劳寿命的交叉项,如式(5)和式(6)所示,以考虑应变比对疲劳寿命的影响以及该影响随疲劳寿命而变化的现象。分别对式(5)和式(6)进行多元线性回归以确定各待定参数,从而可得到一种能考虑应变比影响以及其影响随寿命而变化的应变寿命模型,如式(7)所示。
| $ \begin{array}{l} {\rm{lg}}\;{\mathit{\varepsilon }_{{\rm{ea}}}}{\rm{ = }}{\mathit{b}_{\rm{e}}}{\rm{ + }}{\mathit{k}_{{\rm{e1}}}}{\rm{lg(2}}{\mathit{N}_{\rm{f}}}{\rm{) + }}{\mathit{k}_{{\rm{e2}}}}{\rm{lg}}\left( {\frac{{1 - \mathit{R}}}{2}} \right){\rm{ + }}\\ \;\;\;\;\;\;\;\;\;\;\;\;{\mathit{k}_{{\rm{e3}}}}{\rm{lg(2}}{\mathit{N}_{\rm{f}}}{\rm{)lg}}\left( {\frac{{1 - \mathit{R}}}{2}} \right) \end{array} $ | (5) |
| $ \begin{array}{l} {\rm{lg}}\;{\mathit{\varepsilon }_{{\rm{pa}}}}{\rm{ = }}{\mathit{b}_{\rm{p}}}{\rm{ + }}{\mathit{k}_{{\rm{p1}}}}{\rm{lg(2}}{\mathit{N}_{\rm{f}}}{\rm{) + }}{\mathit{k}_{{\rm{p2}}}}{\rm{lg}}\left( {\frac{{1 - \mathit{R}}}{2}} \right){\rm{ + }}\\ \;\;\;\;\;\;\;\;\;\;\;\;{\mathit{k}_{{\rm{p3}}}}{\rm{lg(2}}{\mathit{N}_{\rm{f}}}{\rm{)lg}}\left( {\frac{{1 - \mathit{R}}}{2}} \right) \end{array} $ | (6) |
| $ \begin{array}{l} {\mathit{\varepsilon }_{\rm{a}}}{\rm{ = }}{\mathit{\varepsilon }_{{\rm{ea}}}}{\rm{ + }}{\mathit{\varepsilon }_{{\rm{pa}}}}{\rm{ = 1}}{{\rm{0}}^{{\mathit{b}_{\rm{e}}}}}{\rm{(2}}{\mathit{N}_{\rm{f}}}{\rm{)}}^{\mathit{k}_{{\rm{e1}}}}{\left( {\frac{{1 - \mathit{R}}}{2}} \right)^{{\mathit{k}_{{\rm{e2}}}}{\rm{ + }}{\mathit{k}_{{\rm{e3}}}}{\rm{lg(2}}{\mathit{N}_{\rm{f}}}{\rm{)}}}}{\rm{ + }}\\ \;\;\;\;\;{\rm{1}}{{\rm{0}}^{{\mathit{b}_{\rm{p}}}}}{{\rm{(2}}{\mathit{N}_{\rm{f}}}{\rm{)}}^{{\mathit{k}_{{\rm{p1}}}}}}{\left( {\frac{{1 - \mathit{R}}}{2}} \right)^{{\mathit{k}_{{\rm{p2}}}}{\rm{ + }}{\mathit{k}_{{\rm{p3}}}}{\rm{lg(2}}{\mathit{N}_{\rm{f}}}{\rm{)}}}} \end{array} $ | (7) |
式中R为应变比,εea,εpa以及εa分别为弹性应变幅、塑性应变幅和总应变幅,be,ke1等8个参量均为与材料相关的拟合参量。式(7)中虽然有8个待定参量,看似复杂,实际上这8个参量均可通过式(5)和式(6)中的多元线性拟合确定,且拟合过程和Manson-Coffin公式中的4个参量的确定方法相似。由式(7)可以看出,应变比对弹性分量的影响与塑性分量的影响不同,且都随着疲劳寿命的变化而变化。
4 新应变寿命模型的验证本文新模型中参数的确定需要至少两组不同应变比下的疲劳试验结果,而现有的应变疲劳试验多数仅在R=-1下进行,具有多组应变比的疲劳试验数据非常有限。为了验证新应变寿命模型的预测精度,本文从已有文献[5, 18, 19]中找到CC450不锈钢、SAE1045钢以及GH4133材料的光滑试棒和中心孔拉伸试件的疲劳试验结果,将其与上述考虑平均应力和平均应变影响的各寿命模型预测结果进行对比分析。由于试验数据不充足,本文无法确定Walker模型中的平均应力影响敏感度参数γ,因此下文中不对Walker修正模型进行寿命计算、对比与分析。
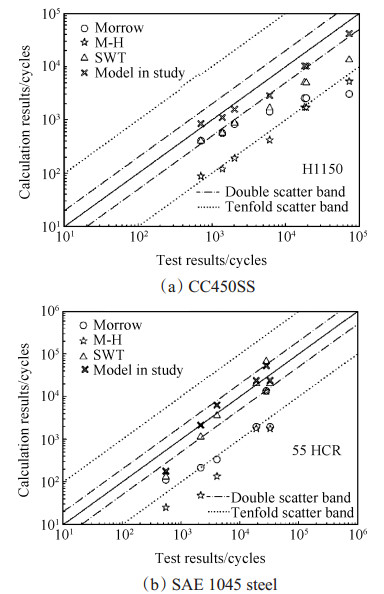
4.1 CC450不锈钢、SAE1045钢疲劳寿命计算结果及验证从已查阅文献中发现CC450不锈钢[18]和SAE1045钢[5]均具有R=0.5,R=0和R=-1三组应变比下的疲劳试验数据。本文采用R=-1组的疲劳试验数据拟合Manson-Coffin方程中的参数,并结合包含平均应力信息的应力参量分别用Morrow弹性修正模型、M-H修正模型和SWT模型计算R=0组的疲劳寿命,并与试验结果进行对比。采用R=0.5和R=-1两组应变比下的疲劳试验数据通过多元线性拟合确定本文新模型中的待定参数,以此计算R=0组的疲劳寿命,并与试验结果以及前述三种方法的计算结果进行对比分析。CC450不锈钢和SAE1045钢在R=0时的各模型疲劳寿命预估结果与试验结果对比分别如图 1所示。
|
Fig. 1 Comparison of fatigue lives calculated by various models with test results for CC450 stainless steel and SAE 1045 steel |
从图 1可以看出,无论是对CC450不锈钢还是SAE1045钢,本文新模型的预测结果精度均最高,基本都分布在2倍分散带内。对于CC450不锈钢,Morrow模型和SWT模型的预测结果相近,均偏安全,且两者均在短寿命区的预测精度较高,而在长寿命时预测精度下降,其预测误差约在2~10倍分散带内;M-H模型的预测结果则明显小于疲劳试验结果,误差分布在10倍分散带左右。对于SAE1045钢,Morrow模型和M-H模型的预测误差均较大,最大误差为试验结果的10倍以上;SWT模型的预测结果相对较好,误差分布在4倍分散带内;同时可以看出,Morrow模型的预测精度在短寿命时较高,而在长寿命时误差增大,这与CC450不锈钢的情况类似。
4.2 GH4133光滑试棒疲劳寿命计算结果及验证试验所用GH4133光滑试棒为直径6mm的标准轴向疲劳拉伸试棒,在250℃下以三角波进行加载,加载频率f=0.33Hz。GH4133材料的基本材料参数如表 1所示。从文献[19]中GH4133材料在R=-1以及R=0.44时的低周疲劳试验数据可以得到MansonCoffin公式与本文新模型中的各参数,如表 2所示。8件光滑试棒均按照应变控制方式加载,最大应变εmax = 1.3426%,最小应变εmin =0.4671%[19]。采用各应变寿命模型计算该载荷下光滑试棒的疲劳寿命,并与试验结果的中位寿命N50%相对比。光滑试棒的疲劳试验结果、各应变寿命模型计算结果以及与试验结果中位寿命的误差如表 3所示。
|
|
Table 1 Main material properties for GH4133 superalloy at 250℃ |
|
|
Table 2 Parameters in Manson-Coffin equation and the new model in this study Parameters |
|
|
Table 3 Experimental and estimated results of various candidate fatigue life calculation models of standard test bars |
从表 3可以看出,M-H修正模型和SWT修正模型均明显低估光滑试棒的疲劳寿命,预测结果偏安全,且M-H模型的预测精度高于SWT模型。Morrow弹性修正模型的预测结果稍大于试验结果,预测结果偏危险。本文新模型对光滑试棒的疲劳寿命预测结果与试验结果最为接近,误差仅有0.25%,效果很好。
4.3 GH4133中心孔拉伸件疲劳寿命计算结果及验证GH4133材料中心孔拉伸件是一个考核部位圆孔与两边加载孔相垂直的拉伸试件,且两边加载孔均与试件中心具有0.1mm的偏心距。试件长90mm,宽23mm,厚20mm,其余细节尺寸见文献[19]。试验过程中,两边加载孔通过销钉与疲劳机连接进行加载,加载波形为三角波,加载频率0.5Hz。
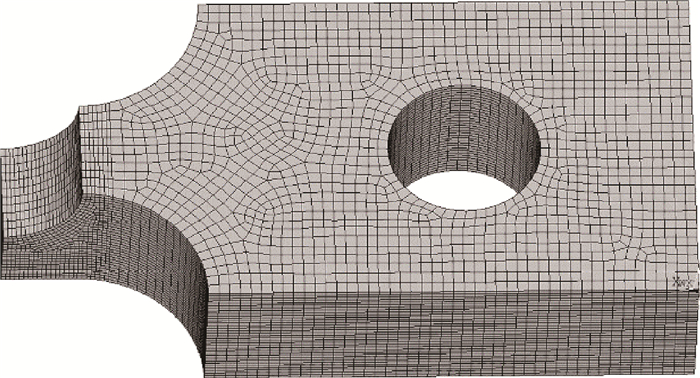
采用ANSYS软件的Solide186单元对中心孔拉伸试件进行有限元分析,共分59304个单元,246665个节点,采用随动强化模型进行弹塑性分析。GH4133中心孔拉伸试件的有限元模型以及有限元计算结果分别如图 2和图 3所示。从图 3可以看出,中心孔边具有一定的应力集中,使得孔边应变较大,但应变沿孔边法向逐渐衰减,且由于孔边危险部位已经进入塑性区,卸载后孔边存在明显的残余应变。
|
Fig. 2 1/4 FE model of the tension specimen with centerhole |

|
Fig. 3 First principle strain of the tension specimen with center-hole |
由图 3可以看出,加载条件下中心孔边的最大应变为1.4%,卸载时残余应变为0.46%,显然在加卸载过程中该孔边存在正平均应变。因此计算该试件的疲劳寿命时需要考虑平均应变对疲劳寿命的影响。中心孔拉伸试件的疲劳试验结果、各应变寿命模型预估结果以及与试验中值寿命的误差见表 4。
|
|
Table 4 Experimental and estimated results of various candidate fatigue life calculation models for tension specimen with center-hole |
同光滑试棒的计算结果相似,M-H修正模型以及SWT修正模型的计算寿命仍然低于中心孔拉伸试件的试验结果,且M-H模型的精度较高。Morrow弹性修正模型的计算结果偏高,同时精度也较高。本文新模型的计算结果偏低,但也与试验结果最为接近。
5 讨论 5.1 各种考虑平均应力效应寿命模型的对比通过采用各考虑平均应力和平均应变影响的应变寿命模型计算CC450不锈钢、SAE1045钢和GH4133材料的光滑试棒以及中心孔拉伸试件的疲劳寿命并与试验结果对比,可以看出,本文新模型的预测精度最高:对CC450不锈钢和SAE1045钢的预测精度基本在2倍分散带内,对GH4133高温合金光滑试棒疲劳寿命的预测结果与试验结果基本相同,而对中心孔拉伸试件的预测结果仅比试验结果小3.67%,表现出了很好的预测有平均应变影响的疲劳寿命的能力。同时,尽管Morrow模型和M-H模型在计算GH4133材料的疲劳寿命时表现出较高的精度,但在预测CC450不锈钢和SAE1045钢时均产生了很大的误差,说明这两种方法在计算不同材料的疲劳寿命时稳定性较差。SWT模型无论在预测CC450不锈钢、SAE1045钢还是GH4133高温合金的疲劳寿命时,其预测精度均可接受,且具有较好的稳定性,因此在疲劳试验数据相对缺乏(仅有R=-1时的疲劳数据)时,SWT模型可作为一种有效的疲劳寿命计算模型。
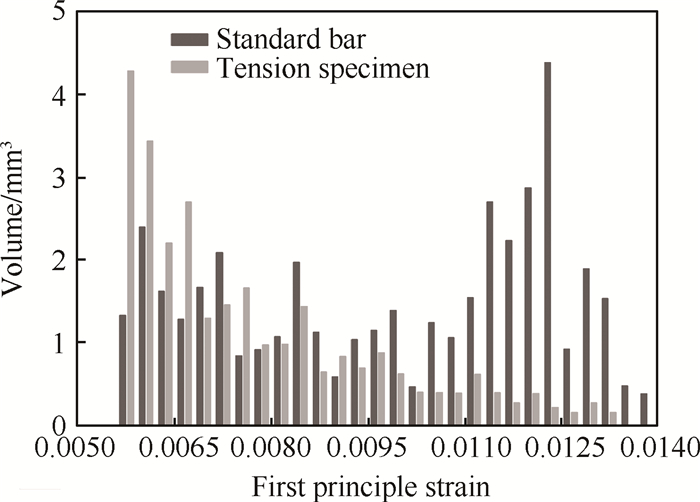
一般而言,构件的疲劳破坏具有明显的体积效应,即在相同的循环应力应变状态下,危险体积越大,构件越容易发生破坏。图 4展示了中心孔拉伸试件与光滑试棒在最危险点加卸载应变状态相同的情况下的危险体积对比(仅考虑应变较大的危险区域)。可以看出,由于中心孔拉伸试件存在应力集中,而光滑试棒的应变分布相对比较均匀,导致中心孔附近大应变区危险体积明显小于光滑试棒的危险体积;而在应变较小区域,中心孔拉伸试件的危险体积又大于光滑试棒。从疲劳破坏的机理来看,大应变区对构件的疲劳破坏起主要影响,而小应变区的作用则相对有限。因此,从体积效应可以推断,中心孔拉伸试件的疲劳寿命应该大于与其最危险点加卸载应变状态相同的光滑试棒。由于本文上述四种寿命模型均基于光滑试棒的疲劳试验数据,并未考虑体积效应,因此计算所得结果为对应载荷状态下的光滑试棒的疲劳寿命。本文模型对中心孔试件疲劳寿命的计算结果低于试验结果,与上述分析相符。相比而言,Morrow弹性修正模型的计算结果大于试验结果,预测结果偏危险。
|
Fig. 4 Comparison of dangerous volumes from standard bar and tension specimen with vertical center-hole |
从上文的计算及分析结果来看,本文新模型具有较高的疲劳寿命预测精度。因此本文模型可作为一种比较可靠的考虑应变比影响的疲劳寿命计算模型。为了进一步研究应变比对疲劳寿命的影响,在本文模型的基础上,以GH4133材料光滑试棒为例,计算了其在不同的应变幅下应变比从R=-1变化到R=0.5的疲劳寿命,如图 5所示。图 5以应变比R为横坐标,以任意应变比下的疲劳寿命Nf与该应变幅下应变比R=-1时(即对称载荷下)的疲劳寿命Nf, -1的比值为纵坐标,以体现应变比对疲劳寿命的影响。从图 5可以看出,在相同的应变幅下,随着应变比的增大,平均应变对疲劳寿命的影响增大。同时,在大载荷下平均应变对疲劳寿命的影响较小,而小载荷下平均应变对疲劳寿命的影响较大。

|
Fig. 5 Effects of strain ratio on fatigue life at various strain amplitudes |
通过对考虑应变比影响的非对称应变寿命模型研究,得到以下结论:
(1) Morrow弹性修正模型和M-H修正模型的预测精度随材料而变化,稳定性较差;SWT模型的预测精度一般,但具有较好的稳定性。
(2) 本文新模型对CC450不锈钢、SAE1045钢的预测结果基本分布在2倍分散带内;对GH4133高温合金的光滑试棒疲劳寿命的预测结果与试验结果仅相差0.25%,两者基本相同;对中心孔拉伸试件的疲劳寿命预测结果比试验结果小3.67%,展示出很好的考虑应变比影响的疲劳寿命预测能力。
(3) 本文新模型需要至少两组不同应变比下的疲劳试验数据进行多元线性拟合以确定模型参数,对试验数据要求较高;在仅有R=-1下的试验数据时,建议使用SWT修正模型。
(4) 在应变幅相同的情况下,随着应变比的增大,平均应变对疲劳寿命的影响增大;同时,在大载荷下平均应变对疲劳寿命的影响相对较小,反之亦然。
(5) 轮盘盘心低循环疲劳应变特征为,首次加载危险点进入屈服,弹性卸载后危险点存在残余应变,且后续加载应变幅基本不变,因此盘心危险部位一般具有正的平均应变和应变比。循环应力应变曲线塑性段斜率越“平”,首次加载进入屈服越深,卸载后应变比越大,从而平均应变对疲劳寿命的影响越大。当然首次加载进入屈服越深,也意味着载荷较大,应变幅相应增大,从而部分减小了平均应变对疲劳寿命的影响。
| [1] |
Ince A. A Mean Stress Correction Model for Tensile and Compressive Mean Stress Fatigue Loadings[J]. Fatigue & Fracture of Engineering Materials & Structures, 2016, 39: 1-10.
(  0) 0) |
| [2] |
Kujawski D. On Deviatoric Interpretation of Neuber's Rule and the SWT Parameter[J]. Theoretical & Applied Fracture Mechanics, 2014, 67: 95-102.
(  0) 0) |
| [3] |
Zhu Shun-Peng, Qiang Lei. Mean Stress Effect Correction in Strain Energy-Based Fatigue Life Prediction of Metals[J]. International Journal of Damage Mechanics, 2016(1): 1-23.
(  0) 0) |
| [4] |
Walker K. The Effect of Stress Ratio during Crack Propagation and Fatigue for 2024-T3 and 7075-T6 Aluminum[R]. ASTM STP 462.
(  0) 0) |
| [5] |
Wehner T, Fatemi A. Effects of Mean Stress on Fatigue Behavior of a Hardened Carbon Steel[J]. International Journal of Fracture, 1991, 13(3): 241-248.
(  0) 0) |
| [6] |
Yung-Li Lee, M E Barkey, Hong-Tae Kang. Metal Fatigue Analysis Handbook: Practical Problem-Solving Techniques for Computer-Aided Engineering[M]. UK: Butterworth Heinemann Ltd, 2012.
(  0) 0) |
| [7] |
米丰. 平均应变对某航空铝合金力学行为影响与随机疲劳寿命预测研究[D]. 杭州: 浙江大学, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10335-1014173380.htm
(  0) 0) |
| [8] |
桑多尔著BI, 俞炯亮译. 循环应力与循环应变的基本原理[M]. 北京: 科学出版社, 1985.
(  0) 0) |
| [9] |
牟园伟, 陆山. 轮盘低周疲劳概率寿命预估模型[J]. 推进技术, 2012, 33(2): 288-292. (MOU Yuan-wei, LU Shan. Low Cycle Fatigue Probabilistic Life Prediction Models for Fan Disk[J]. Journal of Propulsion Technology, 2012, 33(2): 288-292.)
(  0) 0) |
| [10] |
商体松, 赵明, 陈养惠. 基于三参数幂函数的低周疲劳寿命预测方法研究[J]. 推进技术, 2015, 36(6): 907-911. (SHANG Ti-song, ZHAO Ming, CHEN Yang-hui. Low Cycle Fatigue Life Prediction Method Based on Three Parameter Power Function[J]. Journal of Propulsion Technology, 2015, 36(6): 907-911.)
(  0) 0) |
| [11] |
Socie D F, Morrow J D. Review of Contemporary Approaches to Fatigue Damage Analysis[C]. New York: Risk and Failure Analysis for Improved Performance and Reliability, 1980.
(  0) 0) |
| [12] |
Manson S S, Halford G R. Practical Implementation of the Double Linear Damage Rule and Damage Curve Approach for Treating Cumulative Fatigue Damage[J]. International Journal of Fracture, 1981, 17: 169-172. DOI:10.1007/BF00053519
(  0) 0) |
| [13] |
Ince A, Glinka G. A Modification of Morrow and SmithWatson-Topper Mean Stress Correction Models[J]. Fatigue & Fracture of Engineering Materials & Structures, 2011, 34: 854-867.
(  0) 0) |
| [14] |
Fash J, Socie D F. Fatigue Behavior and Mean Effects in Grey Cast Iron[J]. International Journal of Fatigue, 1982, 4(3): 137-142. DOI:10.1016/0142-1123(82)90040-8
(  0) 0) |
| [15] |
Forsett P, Blasarin A. Fatigue Behavior of Microalloyed Steels for Hot-Forged Mechanical Components[J]. International Journal of Fatigue, 1988, 10(3): 153-161. DOI:10.1016/0142-1123(88)90057-6
(  0) 0) |
| [16] |
Koh S K, Stephens R I. Mean Stress Effects on Low Cycle Fatigue for a High Strength Steel[J]. Fatigue & Fracture of Engineering Materials & Structures, 1991, 14: 413-428.
(  0) 0) |
| [17] |
Dowling N E. Mean Stress Effects in Strain-Life Fatigue[J]. Fatigue & Fracture of Engineering Materials & Structures, 2009, 32: 1004-1019.
(  0) 0) |
| [18] |
Lin C K, Chu C C. Mean Stress Effects on Low-Cycle Fatigue for a Precipitation-Hardening Martensitic Stainless Steel in Different Tempers[J]. Fatigue & Fracture of Engineering Materials & Structures, 2000, 23: 545-553.
(  0) 0) |
| [19] |
鲁华平. 涡轮盘低周疲劳寿命可靠性分析及试验评估[D]. 西安: 西北工业大学, 2005. http://cdmd.cnki.com.cn/Article/CDMD-10699-2005064406.htm
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

