航空套齿结构因具有承载能力高、定心性能好、对轴和毂的强度削弱小、结构紧凑等优点,广泛应用于航空发动机结构设计[1]。为了获得更好的气动性能,高压涡轮、高压压气机轴的连接多采用刚性套齿结构限制涡轮转子绕轴线的摆动。而随着加工精度的提高以及转子动力学设计水平的提高,越来越多的高性能发动机的低压涡轮轴与低压压气机轴的连接也采用了刚性套齿结构,如V2500、PW4000系列发动机等。此外,在F101,F404,F110和CFM56等军民用发动机的低压涡轮转子与风扇转子间也普遍采用了刚性套齿结构联轴器。在现代航空发动机整机结构系统设计中,转速的不断提高和结构刚度的不断降低,对转子连接结构力学特征稳定性要求越来越严格[2]。套齿结构的装配特征参数与载荷特征参数对套齿结构的刚度特性与接触状态等力学特征的稳定性有着显著的影响。
目前,国内外对于装配尺寸链及配合公差的分析与稳健性优化发展已比较成熟,主要集中于机械在非运转状态下装配尺寸链及公差配合关系[3~6]。由于没有考虑运转状态下的各零件的变形的影响,静态装配关系设计一般不涉及力学模型,只需建立相应的数学模型,所以问题本身并不十分复杂。但是,当机械处于运转状态下,零件的形状会因受力作用或者温度变化而改变,进而导致各零件之间的装配关系也发生改变,所以针对套齿结构在运转状态下进行动态装配关系的设计很有必要。
当载荷参数、材料参数由于运转、加工等因素呈现不确定性时,装配特征参数也会呈现不确定性。在结构概率分析研究方面,响应面方法能够大大提高结构不确定性设计的计算效率,是复杂结构不确定性设计向工程领域转化的基础。近年来,随着Kriging模型、人工神经网络模型、支持向量机模型、极值响应面模型等在结构概率分析、设计的研究中广泛的应用,结构不确定性优化设计理论与方法研究也在不断深入,从概率方法发展到非概率方法,从单一学科不确定性设计发展到多学科不确定性设计。
本文针对航空发动机套齿结构这一典型连接结构的装配关系,对套齿结构进行了力学特征分析,包括刚度特性分析与接触状态分析,选取了定位面配合紧度与齿侧间隙为装配特征参数。通过有限元方法,计算出套齿结构装配特征参数随载荷特征参数的时变性。建立套齿结构装配特征参数与载荷参数、材料参数的Kriging模型,进行概率分析。建立当量装配质量损失模型,采用果蝇优化算法对套齿结构装配特征参数进行了稳健性优化设计。
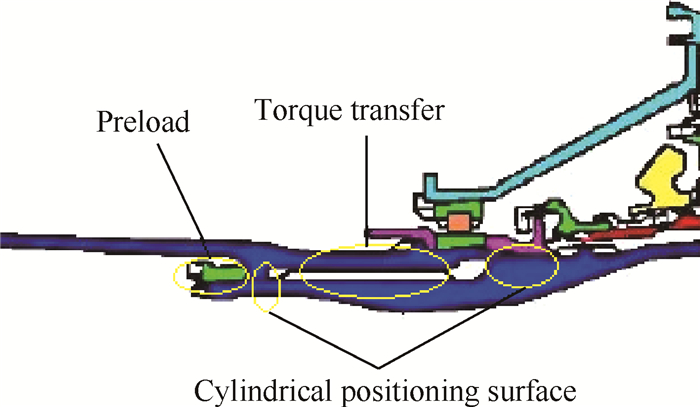
2 套齿结构力学特征分析常用于发动机轴—轴和轴—盘连接的套齿,如图 1所示,其结构力学特征是圆柱面采用一定的紧度配合定心,套齿传递扭矩、大螺母压紧限制两连接轴沿轴向的相对位移,提高连接刚性。从连接刚度方面考虑,定位面配合紧度、定位间距、接触面积等参数都会对套齿连接结构刚度有影响,进而影响转子系统的动力特性,其中尤以定位面配合紧度影响为甚[7]。从套齿结构工程技术要求以及配合质量的方面考虑,齿侧间隙是影响装配状态的关键特征参数[8]。
|
Fig. 1 Spline structure |
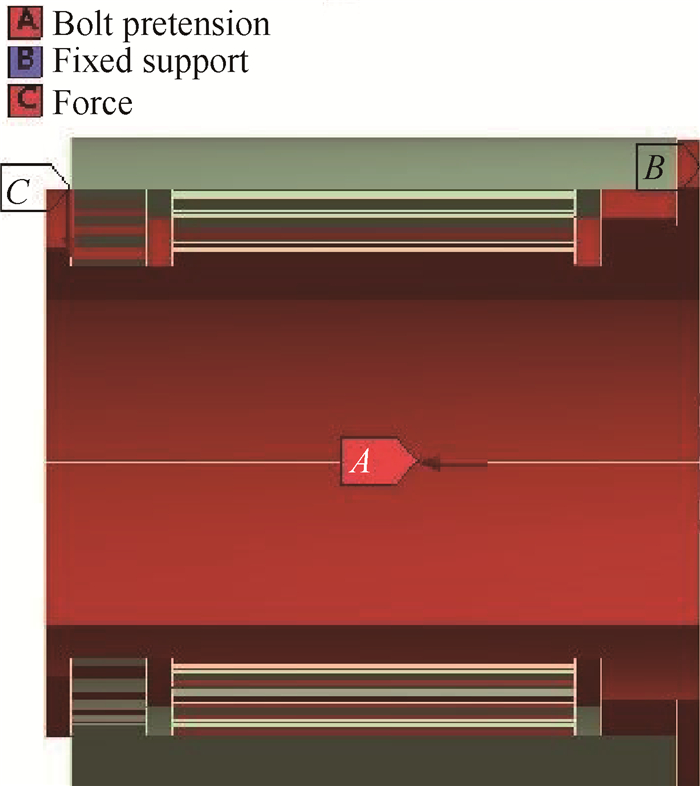
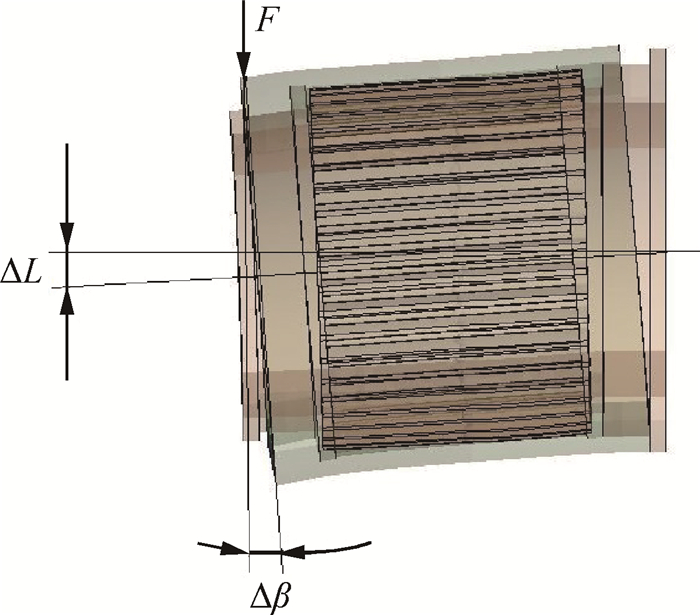
套齿结构连接发动机涡轮轴与压气机轴,主轴的弯曲变形由挠度和转角体现。由于套齿结构存在接触,使得整个轴段存在非连续性,刚度采用整体度量比较适宜。线刚度描述套齿结构抵抗挠度位移的能力,定义为载荷与线位移之比; 角刚度描述套齿结构抵抗角变形的能力,定义为载荷与角位移之比。如图 2、图 3所示,在内套齿一端面B加固定约束,外套齿的另一端面C加力载荷,内套齿内轴面A施加预紧力,得到线刚度为F/ΔL; 角刚度为F/Δβ。这里所研究套齿结构的角刚度与线刚度具有相关性,所以只需研究线刚度与定位面配合紧度的关系。
|
Fig. 2 Spline structure under load |
|
Fig. 3 Stiffness calculation of spline structure |
其它参数不变,分别设定位面配合紧度为0.05,0.10,0.15,0.20mm,计算套齿端面沿着力的方向垂向变形,结果如图 4所示。沿着力F的方向定义为负值,变形的绝对值表征变形量的大小。可以看出,在同样的约束条件下,施加同样的载荷,随着配合紧度的增大,变形量逐渐减少。

|
Fig. 4 Deformation of spline structure |
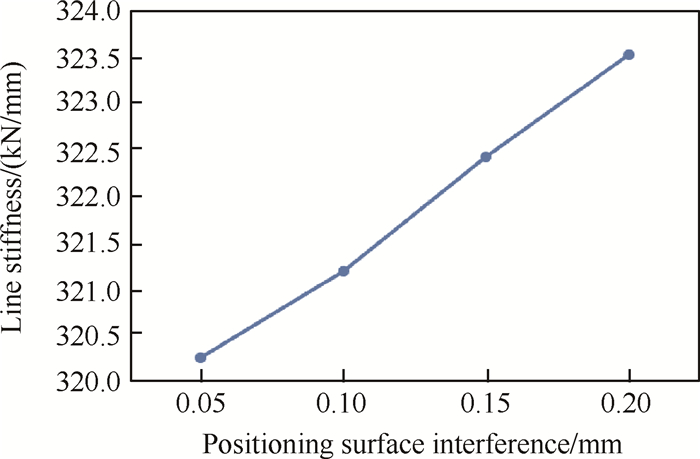
如图 5所示,施加相同载荷,套齿连接刚度随着定位面配合紧度的增大而增大。现有研究表明,增大套齿定位面配合紧度还可以提高套齿结构工作稳定性。
|
Fig. 5 Relation of stiffness and positioning surface interference |
套齿承受弯曲载荷的时候,啮合齿会产生较大的接触应力,应力集中效应在接触面上会很明显。套齿结构的接触状态分析用接触面的应力分布与接触应力最大值来表征。
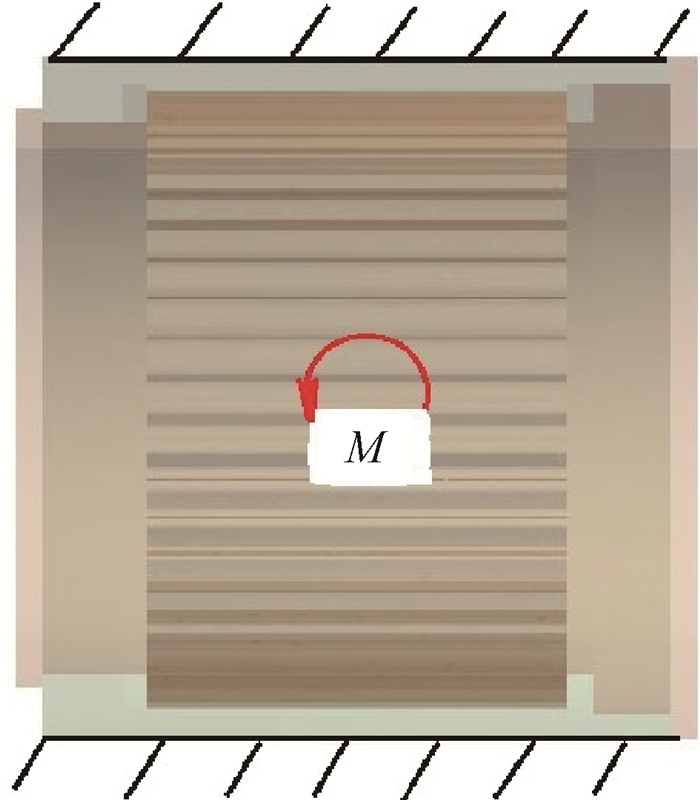
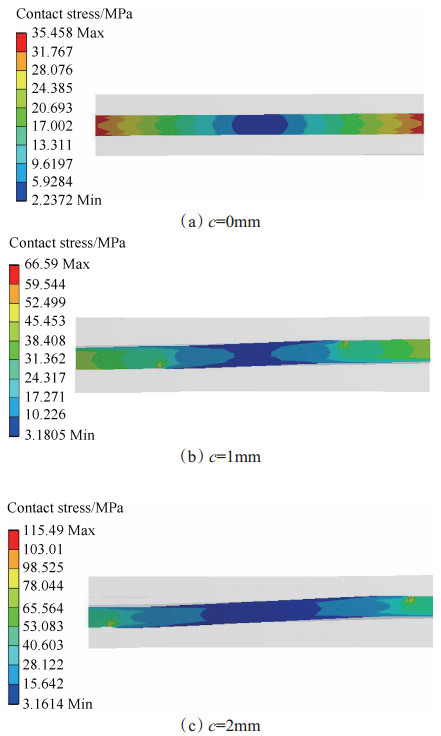
如图 6所示,将外套齿固定,内套齿施加相同弯矩M,齿侧间隙分别为0,1,2mm,垂直于倾角方向的齿接触应力最大,啮合齿的截面应力分布与接触应力最大值如图 7所示。
|
Fig. 6 Contact state of spline structure |
|
Fig. 7 Contact stress |
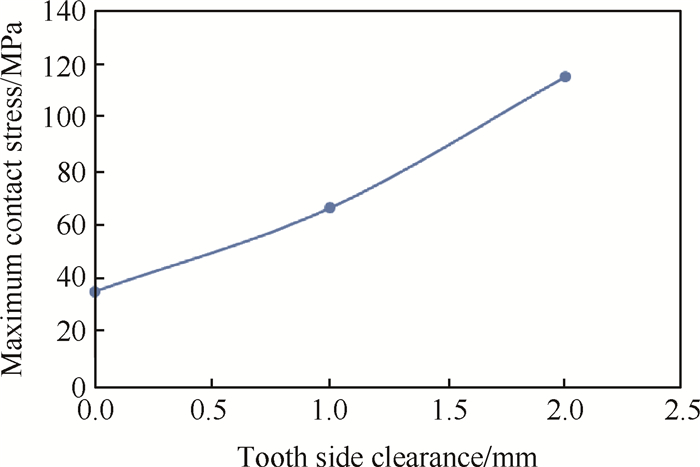
相同载荷与约束条件下,接触应力最大值与齿侧间隙的关系如图 8所示。
|
Fig. 8 Relation between maximum contact stress and tooth side clearance |
可见齿侧间隙越大,啮合齿接触应力越大,产生应力集中。
2.3 装配特征参数分析通过对套齿连接结构进行力学分析,选取齿侧间隙c与定位面配合紧度Δ作为套齿结构动态装配特征参数。航空发动机套齿结构的动态装配特征参数设计对转子装配的复杂度与运转的稳定性具有双刃剑效应。齿侧间隙过大使啮合齿面接触状态不理想,出现应力集中,使得接触应力增大,同时也会造成转子振动变化加大[9],使发动机性能下降; 齿侧间隙过小造成装配困难。圆柱定位面配合紧度过大,使得装配困难并造成装配应力过大; 定位面配合紧度过小,会使套齿连接刚度减小,降低发动机工作的稳定性。套齿结构在受到机械载荷、热载荷发生变形的情况下,动态齿侧间隙和动态定位面配合紧度的装配涉及到内套齿与外套齿之间的协同装配,其装配关系直接决定着发动机转子系统的稳定性和可靠性。因此,选取套齿结构齿侧间隙与定位面配合紧度为套齿装配特征参数,研究装配特征参数在机械载荷、热载荷的作用下随时间变化的规律。
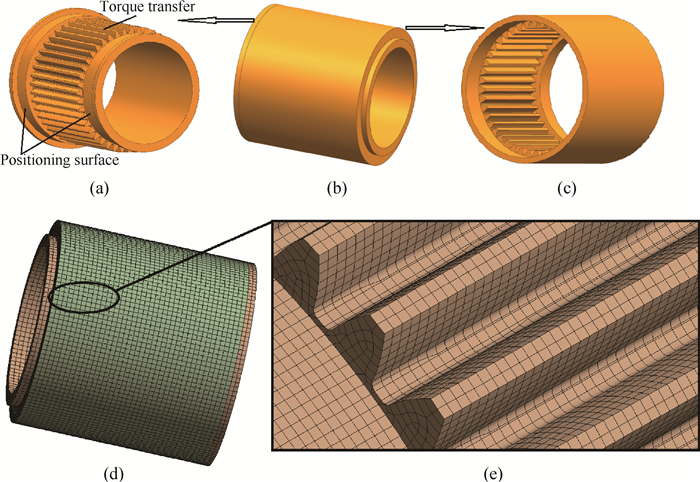
3 动态装配关系时变特性研究 3.1 有限元模型选取发动机高压涡轮轴与压气机轴的套齿联轴器,采用UG建立三维模型,ANSYS建立有限元模型如图 9所示。根据设计手册选取套齿初始装配特征参数:初始齿侧间隙c0=0.1 mm; 初始定位面配合紧度Δ0=18μm。在套齿端面施加扭矩,内外套齿施加转速,内轴面添加预紧力模拟大螺母锁紧,依据结构的尺寸以及所处的安装位置,整体施加均匀温度载荷,固定轴向、周向的自由度,防止产生刚体位移。
|
Fig. 9 Structure model and FE model:(a) external spline, (b) assembly, (c) internal spline, (d) FE model, (e) tooth mesh refinement |
套齿结构所用材料1Cr11Ni2W2MoV的材料性能数据[10]如表 1所示,根据表中数据定义了套齿结构的材料属性。
|
|
Table 1 Material properties of 1Cr11Ni2W2MoV |
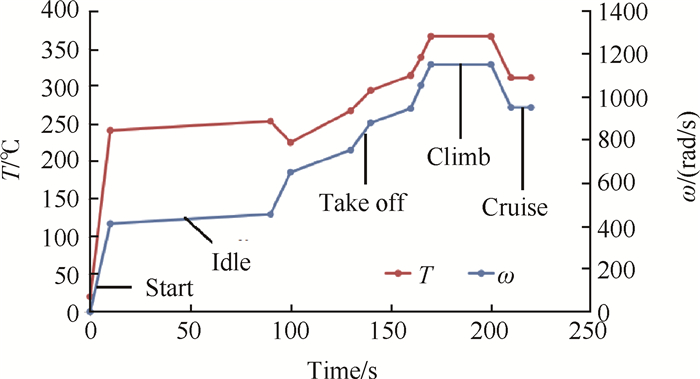
截取航空发动机典型飞行剖面中启动—慢车—起飞—爬升—巡航这一段为计算范围[11~14],选取其中的12个样本点为计算点,绘制温度T、转速ω的载荷谱如图 10所示。
|
Fig. 10 Aero engine flight profile load spectrum |
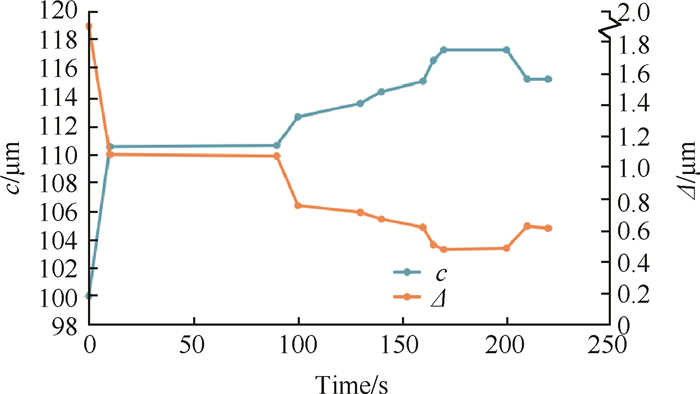
按照载荷谱对有限元模型进行加载,经过对装配对象的仿真计算,得到动态下套齿配合的齿侧间隙c(t)与定位面配合紧度Δ(t)随时间的变化规律,如图 11所示。
|
Fig. 11 Curve of assembly characteristic parameters |
由以上的计算结果可知,在发动机启动—爬升这一阶段里,随着温度、转速升高,c(t)也随之增加,而Δ(t)在减小; 在爬升过程中,c(t)达到了最大,造成啮合齿面接触应力达到最大,而Δ(t)达到了最小值,此时套齿刚度下降,使得转子运转的稳定性降低; 由爬升进入到巡航状态时,c(t)有所减小,Δ(t)也有所增大。因此,套齿结构的配合关系危险时刻是在爬升阶段,热载荷、离心载荷达到最大的时候发生,即t=170s。
将t=170s这一点作为计算点进行概率分析和稳健性优化设计。在t=170s时,套齿结构的动态齿侧间隙和动态定位面配合紧度的分布云图如图 12、所示,齿侧间隙ct=111.724×μm,定位面配合紧度Δt=0.4773μm。对于云图进行说明:数值为正表示过盈,数值为负表示间隙。轴孔配合中,云图中的配合紧度是以轴孔半径之差计量的,而通常所说的配合紧度是以为轴孔直径之差计量的,所以图例的2倍即为实际配合紧度,以下相同,不再赘述。由云图可知,齿侧间隙的分布比较均匀,定位面配合紧度的分布以中间带比较大,向两侧减小,在端部,由于受预紧力的影响而增大。

|
Fig. 12 Simulation results of dynamic tooth side clearance |

|
Fig. 13 Simulation results of dynamic positioning surface interference |
影响航空发动机套齿结构动态齿侧间隙与动态定位面配合紧度的随机输入变量选取转速ω、扭矩M、温度T、密度ρ和弹性模量E。所选取的随机变量及其抽样统计特征如表 2所示,假设表中参数相互独立,均服从正态分布。
|
|
Table 2 Random input parameters for probability analysis |
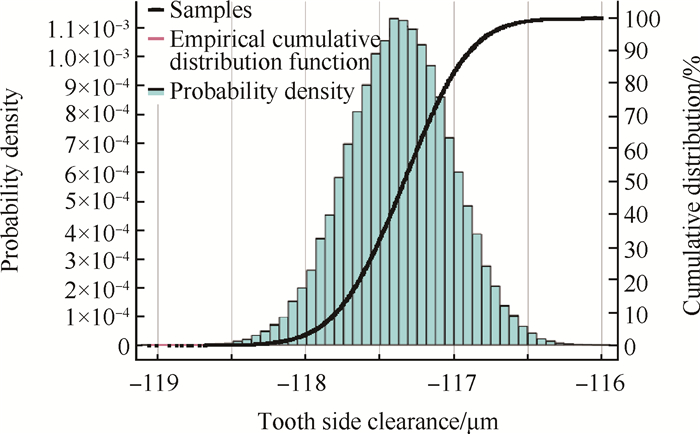
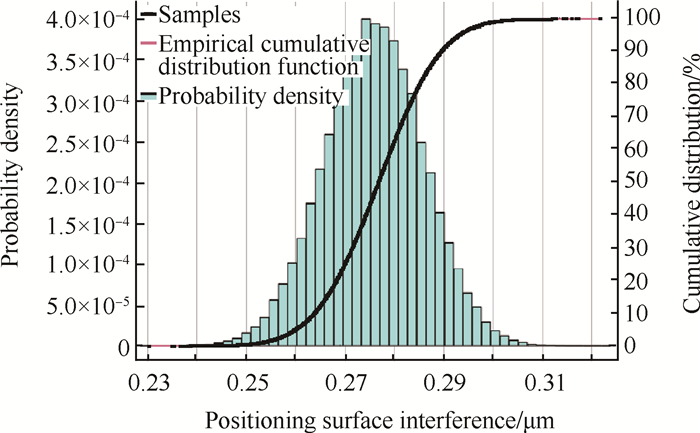
在处理杂非线性问题上Kriging模型相对于神经网络模型和支持向量机模型有着精度和效率上的优势[15]。所以,利用Kriging插值模型,构造结构概率分析的响应面模型。选用拉丁超立方抽样(LHS),借助响应面模型进行1.0×105次抽样,获得套齿结构概率响应分析结果,输出分布直方图及概率分布曲线如图 14和15所示。
|
Fig. 14 Probability distribution of dynamic tooth side clearance |
|
Fig. 15 Probability distribution of dynamic positioning surface interference |
齿侧间隙的均值为117.34μm,标准差为0.35294μm; 定位面配合紧度的均值为0.55358μm,标准差为2.0068×10-5 mm。而3.2节中对套齿结构齿侧间隙与定位面配合紧度的确定性分析结果为齿侧间隙ct=111.724μm,定位面配合紧度Δt=0.4773μm。两种方法分析的装配特征参数的结果有一定的偏差。这是因为确定性分析只经过一次计算具有一定的盲目性,而概率分析经过十万次计算的计算结果相对符合实际,比较精确。
5 稳健性优化设计稳健性设计方法是近年来发展起来的一种工程设计方法,其指导思想是利用输入参数发生微小变差对输出参数影响的不敏感性对产品的质量、性能和成本综合考虑做出最佳设计,从而提高产品质量,降低成本[16],在航空工程中也得到了很好的应用[17~19]。本文建立当量装配质量损失模型对动态下套齿结构装配特征参数进行稳健性优化。
果蝇优化算法(Fruit Fly Optimization Algorithm,FOA)由中国台湾学者潘文超[20]提出的一种新方法,基于果蝇觅食行为而推演出的寻求全局优化的算法。将其原理用于优化算法中,可以避免优化结果陷入局部最优,而且收敛速度快,收到了很好的效果[21]。所以,采用果蝇优化算法对套齿动态装配特征参数进行稳健性优化设计。
5.1 当量装配质量损失模型为了使套齿结构动态装配特征参数对于干扰因素不敏感,同时使得动态齿侧间隙和动态定位面配合紧度尽可能接近目标值,构造装配质量损失模型,通过对两个装配特征量的权衡比重组成装配质量损失函数函数S,装配特征参数偏离目标值的程度越大、分散度越大,则装配质量损失越大
| $ \mathit{S}{\rm{=}}{\mathit{\omega }_{\rm{1}}}{\rm{[(}}{\mathit{\mu }_{\rm{c}}}{\rm{-}}{\mathit{c}_{\rm{g}}}{{\rm{)}}^{\rm{2}}}{\rm{+}}\mathit{\sigma }_{\rm{c}}^2{\rm{]+}}{\mathit{\omega }_{\rm{2}}}{\rm{[(}}{\mathit{\mu }_\mathit{\Delta }}{\rm{-}}{{\rm{\Delta }}_{\rm{g}}}{{\rm{)}}^{\rm{2}}}{\rm{+}}\mathit{\sigma }_\mathit{\Delta }^2{\rm{]}} $ | (1) |
式中ω1, ω2为非负权重系数,满足ω1+ω2=1,根据实际设计考虑的侧重点权衡选取合适的值,这里取齿侧间隙与定位面配合紧度同等程度的优化,取ω1=0.5,如果侧重于优化齿侧间隙可以调整ω1,使之增大,在优化过程中逐步调整至合适的值。对于齿侧间隙与定位面配合紧度来说,动态下的齿侧间隙变大,定位面配合紧度变小,优化的目的是对动态下齿侧间隙的最小值与定位面配合进度的最大值寻优,初始装配值是在现有的加工装配水平下所能达到的最为理想的装配状态,即齿侧间隙最小而定位面配合紧度最大,所以选取cg初始装配的齿侧间隙值,cg=0.1mm,Δg为初始装配的定位面配合紧度值,Δg=0.018 mm,寻优结果能够尽可能向目标值移动。μc, σc为动态齿侧间隙的均值、标准差,μΔ, σΔ为动态定位面配合紧度的均值、标准差。
动态装配特征参数不是一个固定的量值,不同连接结构的装配特征参数也不同。由于装配参数本身的量级不同、加工难易程度、运行状态等造成分散性不同,连接结构装配质量损失差异很大,不具有可比性和通用性。为了更好地描述稳健性优化的效果,现引入一个无量纲量“当量装配质量损失”的概念。当量装配质量损失定义如下
| $ {\mathit{S}_{\rm{r}}}{\rm{=}}\frac{\mathit{S}}{{{\mathit{S}_{\rm{t}}}}} $ | (2) |
Sr为当量装配质量损失,St为t=170s危险点装配质量损失
| $ {\mathit{S}_{\rm{t}}}{\rm{=}}{\mathit{\omega }_{\rm{1}}}{\rm{[(}}{\mathit{\mu }_{{\mathit{c}_{\rm{t}}}}}{\rm{-}}{\mathit{c}_{\rm{g}}}{{\rm{)}}^{\rm{2}}}{\rm{+}}\mathit{\sigma }_{{\mathit{c}_{\rm{t}}}}^2{\rm{]+}}{\mathit{\omega }_{\rm{2}}}{\rm{[(}}{\mathit{\mu }_{{\mathit{\Delta }_{\rm{t}}}}}{\rm{-}}{\mathit{\Delta }_{\rm{g}}}{{\rm{)}}^{\rm{2}}}{\rm{+}}\mathit{\sigma }_{{\mathit{\Delta }_{\rm{t}}}}^2{\rm{]}} $ | (3) |
当0 ≤ Sr<1时,说明起到了优化效果,越接近于零,优化效果越好。
5.2 稳健性优化随机变量的选取在影响套齿结构装配特征参数的输入变量中,一类是噪声变量,这类随机变量在发动机运行过程中不可以或者不便于对其进行控制,只能作为随机输入参数而不能视为待优化参数,扭矩M、密度ρ、弹性模量E属于这类随机变量,记作z =(M, ρ, E)。另外一类是可控变量,在发动机运行的动态过程中可以对其进行主动控制,因此能够作为待优化的参数,可以通过改变其数值来进行寻优,转速ω、温度T属于这类变量,记作x =(ω, T)。通过以上对各参数的灵敏度分析可知,通过优化转速和温度能够达到很好的效果。
考虑到航空发动机的性能要求,转速均值μω的取值范围为[1100, 1200],温度均值μT的取值范围为[350, 390],各输入变量的概率分布情况如表 3所示。各随机变量的分布构成概率空间(Ω, C, P); Ω为随机事件,C为事件的全体,P为事件发生的概率。
|
|
Table 3 Random input parameters for robustness design |
基于当量装配质量损失模型,采用FOA对套齿结构动态装配特征参数进行稳健性优化,目标函数是对当量装配质量损失的最小值进行寻优,约束条件使得各随机变量均在概率空间内。其具体表达式如式(4)所示
| $ \left\{ \begin{array}{l} {\rm{min}}\;\;\;\;\;{\mathit{S}_{\rm{r}}}\\ {\rm{s}}{\rm{.t}}{\rm{.}}\mathit{x}{\rm{, }}\mathit{z} \in {\rm{(}}\mathit{\Omega }{\rm{, }}\mathit{C}{\rm{, }}\mathit{P}{\rm{)}} \end{array} \right. $ | (4) |
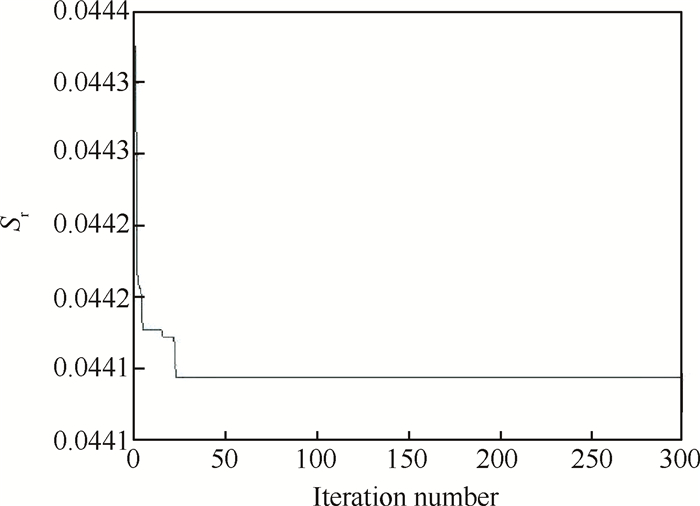
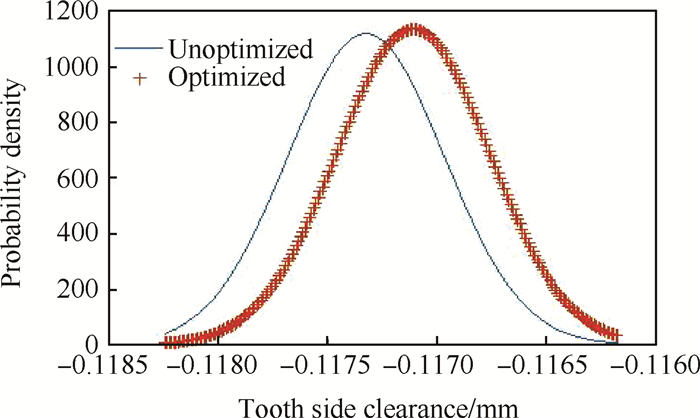
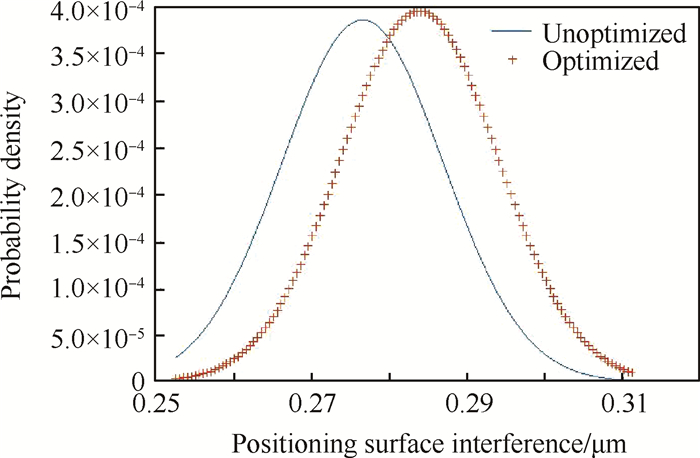
优化过程如图 16所示。可知,在种群迭代到第25代时,目标函数开始收敛。优化前与优化后的概率密度函数分布如图 17、18所示。优化后的ct相对优化前减小,Δt相对优化前增大,ct与Δt的分散性相比之前都有所减小。
|
Fig. 16 Robust optimization process |
|
Fig. 17 Probability density function distribution of dynamic tooth side clearance before and after optimization |
|
Fig. 18 Probability density function distribution of dynamic positioning surface interference before and after optimization |
套齿结构优化前后动态装配特征参数、设计变量与当量装配质量损失数据对比如表 4所示。
|
|
Table 4 Comparison of data before and after optimization |
由表可知,优化后的当量装配质量损失为0.0441,而且各动态装配特征参数向目标值趋近,并且随外载荷及材料参数的波动减小,降低了对随机变量的敏感度,提高了套齿结构动态下配合关系抵抗参数波动干扰能力,使套齿结构动态装配特征参数的设计具有稳健性。
6 结论通过本文研究,得出以下结论:
(1) 增大定位面配合紧度有利于提高套齿结构刚度,增大齿侧间隙有利于降低接触齿面的应力值。计算套齿结构装配特征参数时变特性,得出了齿侧间隙与定位面配合紧度随时间变化的规律,找到了t=170s这一时刻作为计算点进行概率分析与稳健性优化设计。
(2) 通过对装配特征参数进行概率分析,得到了概率分布特征,相比于一次确定性的计算,经过十万次计算的计算结果相对符合实际,比较精确。
(3) 通过对套齿结构装配特征参数稳健性优化设计,当量装配质量损失降为0.041,齿侧间隙减小同时定位面配合紧度增大,并且这两个装配特征参数的标准差都减小,降低了对随机变量的敏感度,提高了连接结构动态下配合关系抵抗参数波动干扰能力,达到了稳健性优化设计的目标。
| [1] |
陈光. 航空发动机结构设计分析[M]. 北京: 北京航空航天大学出版社, 2014, 349-393.
(  0) 0) |
| [2] |
李其汉, 王延荣. 航空发动机结构强度设计问题[M]. 上海: 上海交通大学出版社, 2014, 340-350.
(  0) 0) |
| [3] |
王瑜, 翟文杰, 吴伟国, 等. 公差稳健优化设计的研究[J]. 计算机集成制造系统, 2007, 13(11): 2081-2085. (  0) 0) |
| [4] |
茅健, 曹衍龙. 一种公差敏感稳健性的设计方法[J]. 上海工程技术大学学报, 2011(6). (  0) 0) |
| [5] |
Zhang J, Li S P, Bao N S, et al. A Robust Design Approach to Determination of Tolerance of Mechanical Products[J]. Manufacturing Technology, 2010, 59(1): 195-198.
(  0) 0) |
| [6] |
Siva Kumar M, Islam M N, Lenin N, et al. Optimum Tolerance Synthesis for Complex Assembly with Alternative Process Selection Using Lagrange Multiplier Method[J]. International Journal of Engineering, 2010, 3(4): 380-402.
(  0) 0) |
| [7] |
李俊慧, 洪杰. 转子连接结构动力学设计方法与实验研究[D]. 北京: 北京航空航天大学, 2009.
(  0) 0) |
| [8] |
刘永福. 航空发动机构造[M]. 北京: 国防工业出版社, 1995, 194-201.
(  0) 0) |
| [9] |
孙义冈, 陈耿, 李伟华. 齿套联轴器对汽轮机轴系振动的影响[J]. 动力工程, 1991, 11(6): 21-23. (  0) 0) |
| [10] |
航空发动机设计手册总编委会. 航空发动机设计手册. (第18分册), 叶片轮盘及主轴强度分析[M]. 北京: 航空工业出版社, 2001, 371-376.
(  0) 0) |
| [11] |
Annette E N, Christoph W M, Stehan S. Modeling and Validation of the Thermal Effects on Gas Turbine Transients[J]. Journal of Engineering for Gas Turbines and Power, 2005, 127(3): 564-572. DOI:10.1115/1.1850495
(  0) 0) |
| [12] |
Pilidis P, Maccallum N R L. Models for Predicting Tip Clearance Changes in Gas Turbines[R]. NASA, N83-29258.
(  0) 0) |
| [13] |
Lattime S B, Steinetz B M. Turbine Engine Clearance Control Systems: Current Practices and Future Directions[J]. Journal of Propulsion and Power, 2004, 20(2): 302-311. DOI:10.2514/1.9255
(  0) 0) |
| [14] |
费成巍, 白广忱, 赵合阳, 等. 高压涡轮叶尖径向运行间隙概率设计[J]. 北京航空航天大学学报, 2013, 39(3): 305-309. (  0) 0) |
| [15] |
陈志英, 任远, 白广忱, 等. 粒子群优化的Kriging近似模型及其在可靠性分析中的应用[J]. 航空动力学报, 2011, 26(7): 1522-1530. (  0) 0) |
| [16] |
陈立周. 稳健设计[M]. 北京: 机械工业出版社, 1999, 2-67.
(  0) 0) |
| [17] |
贺谦, 李元生, 温志勋, 等. 涡轮叶片多学科可靠性及稳健设计优化[J]. 推进技术, 2010, 31(2): 193-197. (HE Qian, LI Yuan-sheng, WEN Zhi-xun, et al. Multidisciplinary Reliability and Robust Design Optimization for Turbine Blades[J]. Journal of Propulsion Technology, 2010, 31(2): 193-197.)
(  0) 0) |
| [18] |
韩小宝, 王仲生. 航空发动机鲁棒线性变参数滤波器设计[J]. 推进技术, 2009, 30(2): 209-212. (HAN Xiao-bao, WANG Zhong-sheng. Robust Linear Variable Parameter Filter Design for Aeroengine[J]. Journal of Propulsion Technology, 2009, 30(2): 209-212.)
(  0) 0) |
| [19] |
鲍文, 常军涛, 马照祥, 等. 涡扇发动机转速鲁棒控制器设计及试验[J]. 推进技术, 2005, 26(2): 158-161. (BAO Wen, CHANG Jun-tao, MA Zhao-xiang, et al. Turbofan Engine Speed Controller Design and Test[J]. Journal of Propulsion Technology, 2005, 26(2): 158-161.)
(  0) 0) |
| [20] |
Pan W T. A New Fruit Fly Optimization Algorithm: Taking the Financial Distress Model as an Example[J]. Knowledge Based Systems, 2012, 26(2): 69-74.
(  0) 0) |
| [21] |
周平, 白广忱. 基于神经网络与果蝇优化算法的涡轮叶片低循环疲劳寿命健壮性设计[J]. 航空动力学报, 2013, 28(5): 1013-1018. (  0) 0) |
 2018, Vol. 39
2018, Vol. 39

