现代战争中的电子对抗,各种雷达探测技术、雷达制导武器的快速发展,使得飞行器尾向隐身成为提高飞机生存力的重要因素[1]。喷管作为典型电大腔体结构,是飞机尾向强雷达散射源,对飞机的整体雷达散射截面(RCS)贡献巨大。因此,对喷管的RCS特性进行计算分析具有重要的军事意义。
近年来,相关学者已经开始重视并开展了该方面的研究[2~10]。文献[2~7]分别对轴对称喷管、二元喷管以及球型收敛喷管的RCS特性进行了数值模拟,结论表明,二元喷管的宽高比[4]以及喷管的出口形状[3]对喷管的RCS有影响;合理的雷达吸波材料涂覆方案可以有效缩减RCS,并降低吸波材料的使用量[7]。李岳峰等[8]、郭宵等[9]以及高翔等[10],分别对S形进排气系统的RCS特性进行了计算分析,结论表明S形进气系统的进口形状[8],排气系统的出口宽高比[9]对系统的RCS有较大影响;而合理的介质涂覆方案可以有效地抑制系统的RCS,同时兼顾经济性、重量,并且涂覆方便[10]。
区别于上述研究对象,本文着力于新型加有塞锥的排气系统的RCS特性数值模拟和分析。塞式喷管可以通过改变塞锥的几何形状以及轴向位置来调节喷管的喉道与出口面积,使得发动机能在不同的工况下正常工作;塞锥与喷管壁的相互配合还可以实现发动机的矢量和反推功能;在航天领域,塞式喷管因其高度补偿能力可被用于可重复使用单级入轨火箭发动机;因而塞式喷管受到了航空航天领域众多研究者的关注[11~14]。国内外先后有Hiley等[15]、Banken等[16]、Chu等[17]、戴梧叶等[18]、王长辉等[19]以及陈俊[20]对塞式喷管的气动和红外辐射特性开展了数值和试验方面的大量研究工作,结果表明,塞锥的存在确实会降低喷管的效率至90%~96%[18, 19],但塞式喷管的高补偿特性[18, 19]以及塞锥对喷管内部热部件的有效遮挡使其在红外隐身方面产生的优势[20]都使得塞式喷管在航空航天领域有着独特的使用价值。根据几何学和物理学知识推断,喷管内塞锥的存在极有可能有效遮挡喷管内的各种镜面反射回波,从而削弱喷管对飞机总的RCS的贡献,有利于军用飞机的雷达隐身;因而对塞式喷管的雷达隐身研究也有着重要的军事意义。
本文以涡扇发动机尾喷管为参考,设计了轴对称塞式喷管,采用物理光学迭代法(IPO)[2, 21]和等效边缘电磁流方法(EEC)[22, 23]对喷管腔体散射场和棱边绕射场进行计算分析,研究了不同锥度的塞锥对喷管RCS特性的影响。
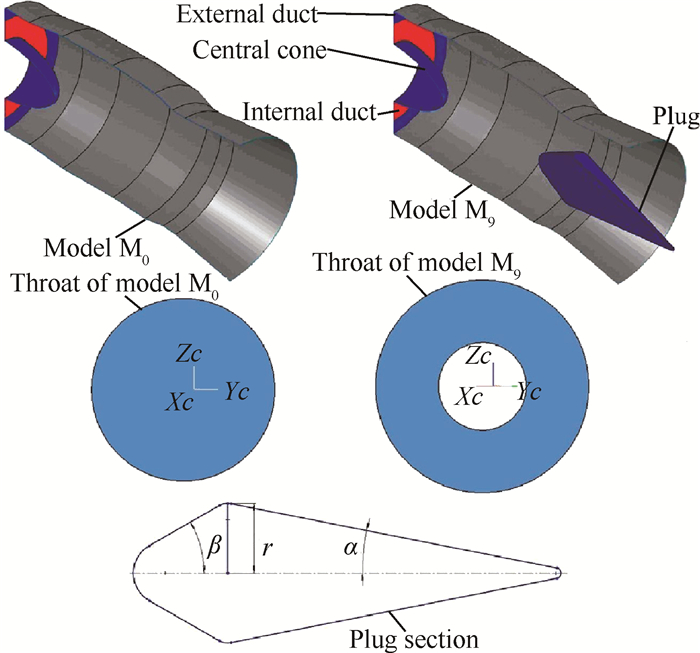
2 物理模型和计算方法 2.1 物理模型以涡扇发动机尾喷管为蓝本,改型设计了九型塞式喷管。为了与基准喷管进行比较分析,塞式喷管的喉道和出口流通面积保持与原喷管一致,塞锥由前锥与后锥组合光滑过渡而成。本文根据参考文献[20]中塞锥几何参数对气动和红外特性影响分析以及本课题组在喷管后部几何形状对电磁散射特性影响方面的研究,塞锥设计参数选择为:塞锥前锥半锥顶角β固定为30°,塞锥半径比固定为0.5(塞锥最大半径r与内涵进口半径R之比)[20],塞锥后锥半锥顶角α分别为7.5°,10°,11.25°,13°,15°,17°,18.75°,20°,22.5°。所有喷管分别编号,不加塞锥的轴对称喷管编为M0号,依次随α的递增,喷管编号为M1~M9,如表 1所示。图 1为原始喷管与加塞喷管的对比,以及塞锥剖面的示意图。
|
|
Table 1 RCS comparison of different plug nozzles |
|
Fig. 1 Illustration of original nozzle, plug nozzle and the plug section |
本文的电磁散射特性采用自主开发程序进行计算。程序主要采用物理光学迭代法(IPO)对腔体雷达散射特性进行模拟,采用等效边缘电磁流方法(EEC)对喷管棱边绕射场进行模拟。
由于喷管的进口端有高速旋转涡轮,仅有少量的电磁波能够穿越涡轮,因此可将进口端视为壁面,作短路处理,即喷管作为单端开口腔体进行计算。
2.2.1 物理光学迭代法(IPO)物理光学迭代法是分析腔体散射特性的一种行之有效的高频近似方法,这种方法能够有效模拟目标对电磁波的多次反射,从金属表面的磁场积分方程出发,进行迭代求解出表面电流的分布,进而求解其电磁散射特性。
2.2.2 等效边缘电磁流方法(EEC)等效边缘电磁流法的概念是将边缘等效为电(磁)流源[24]。这种方法主要是将等效边缘电(磁)流与边缘绕射场联系起来,用前者的辐射场来近似焦散区边缘绕射场,从而求解焦散处的场值。其基本思路是假设在环绕表面奇异性(边缘回路)的各点处存在线电流I和线磁流M,通过远场辐射积分形式对I和M求和,得到绕射场场值。
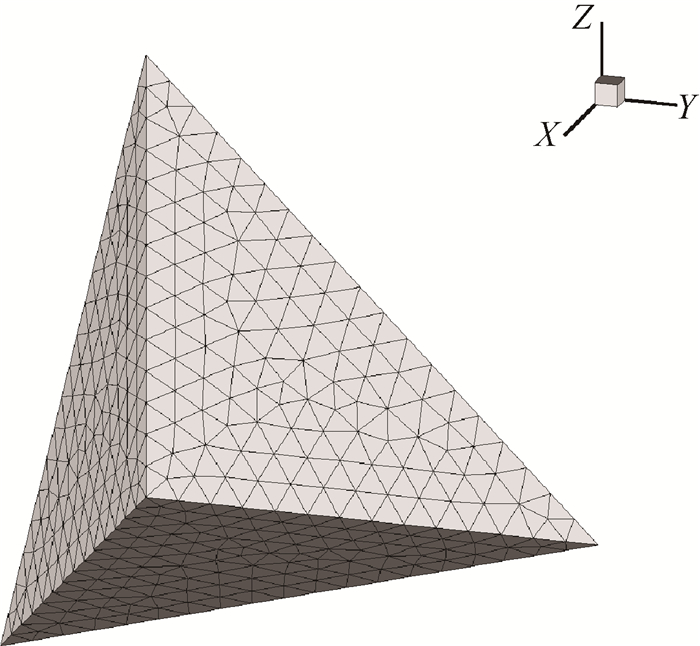
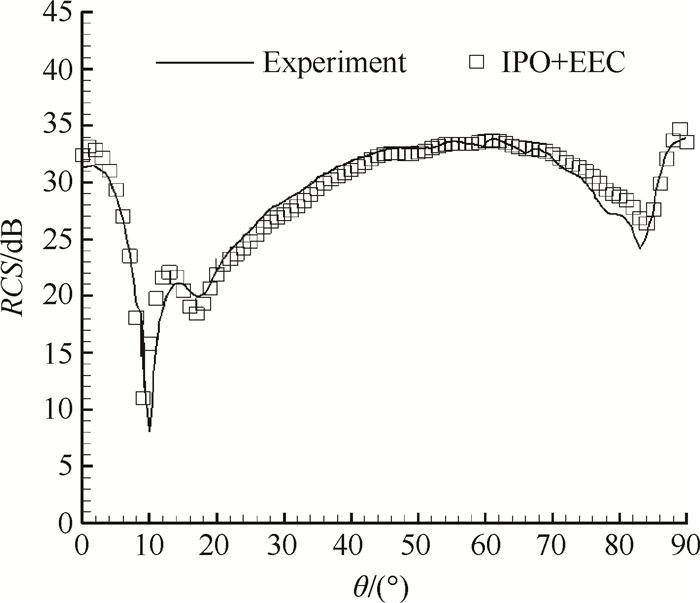
2.2.3 程序校验为了验证本文计算方法的正确性,以文献[25]中三角形三面角反射器为对象,计算其电磁散射特性,并与实验数据[25]对比。图 2所示为该模型形状及网格划分,组成其顶角的三个棱边长度均为5λ,其中λ为入射波长。图 3是其水平极化方式下总场RCS计算结果与相应实验数据的对比曲线,由图可以看出,使用本程序计算的结果与文献中实验数据吻合相当好。
|
Fig. 2 Geometry and mesh of triangle trihedral corner reflector |
|
Fig. 3 RCS of trihedral corner reflector(experimental data from Ref. [25]) |
本文计算了十种模型的RCS,包括原喷管和九种加塞喷管,腔体内壁均视为理想导电体。计算的重点仰俯角[1]范围为-40°~40°,其中正值表示俯视照射,负值表示仰视照射。入射波波长为λ(物理模型特征尺寸10λ),计算分析了水平极化和垂直极化两种极化方式下,不同形状塞锥对喷管单站RCS特性的影响规律。
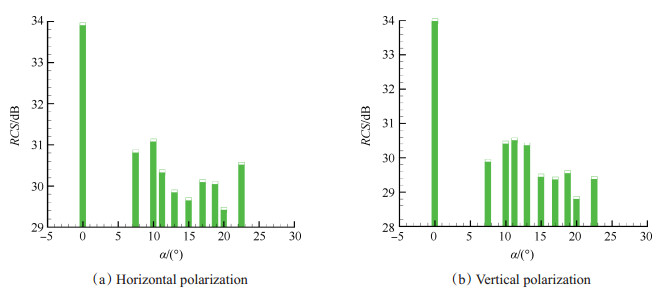
3.1 各模型RCS均值分析表 1是加不同形状塞锥的喷管雷达散射总场RCS在-40°~40°仰俯角范围内的算术平均值以及各模型喷管RCS均值相对原喷管的减小百分率,其中M0号模型为不加塞锥原始尺寸喷管。由表可以看出,在两种极化方式下,所有加塞喷管都比原喷管的RCS值有所减小。这主要是因为塞锥在某些仰俯角范围内有效遮挡了喷管进口处简化平面的镜面反射回波,从而使得加塞锥喷管的RCS均值比不加塞锥的小。图 4是两种极化方式下喷管的总场RCS均值随α增大的变化柱状图。由图可以看出,两种极化方式下,加塞锥都能有效降低喷管的RCS,并且在两种不同极化方式下,喷管模型M8(α=20°)的RCS减缩效果均最好:与原喷管相比,水平极化方式下可减小4.48dB,减小13.2%;垂直极化方式下可减小5.18dB,减小15.2%。
|
Fig. 4 Averaged RCS of different plug nozzles |
图 5是M0~M9模型总场RCS随仰俯角的变化曲线,其中黑色加粗曲线为原喷管的RCS分布。从图中可以看出,各模型的RCS总场曲线基本不按0°仰俯角对称,原因是该型喷管具有5°安装角。从图中还可看出,在0°仰俯角附近,所有喷管模型RCS都会出现一个较强且较宽的波峰,这是因为在0°仰俯角附近,雷达入射波会在涡轮端壁面形成很强的垂直入射镜面反射波,因此在此仰俯角范围内喷管RCS值较大。另外,在0°仰俯角附近,加塞锥的各型喷管RCS值较不加塞锥喷管略有增大。这是因为加塞锥在0°仰俯角附近不仅不能有效遮挡涡轮端壁面的强镜面反射,而且由于塞锥与喷管壁面的耦合作用,散射回波加强,使得RCS值更高。为了更清楚地了解其雷达散射特性,本文取两种极化方式下0°仰俯角附近RCS峰值最大(在水平极化和垂直极化方式下分别比原喷管增大8.14%,11.77%)的M1模型与原始喷管模型M0进行比较。

|
Fig. 5 RCS of different models |
图 6分别为水平极化与垂直极化0°仰俯角时喷管壁面感应电流面密度(Φ)分布云图。从图中可以看出,加塞锥导致原中心锥表面感应电流密度局部变大,由此可见,由于塞锥与喷管壁面多次反射耦合作用,使得喷管中心锥上的感应电流密度增大,从而造成其回波也相应增大,导致喷管0°仰俯角时的RCS值比不加塞锥喷管略大。由图 5可看出,加塞锥模型在重点仰俯角范围内几乎都能达到减缩喷管RCS的目的:对于两种不同极化方式,在多个仰俯角的波峰处,幅值都有大幅度的降低;同时在多个仰俯角处也有相对原型喷管RCS值低得多的波谷,这与均值特征一致。

|
Fig. 6 Induction current comparison of model M1 and original one |
从均值表中可以看出,塞式喷管M8(α=20°)在两种极化方式下RCS均最小。为此,取M8模型与原始喷管进行比较分析。图 7为M0,M8模型总场RCS随仰俯角变化曲线。由于M8模型塞锥末端并未超出喷口,因此M0与M8模型喷管出口边缘形状、尺寸均一致,计算结果也表明两者的出口边缘绕射场RCS数值相同,因而在总场中其变化原因主要是喷管腔体散射场的差别。

|
Fig. 7 RCS comparison of model M8 and original one |
从图中可以看出,在-10°~-22°以及19°~40°仰俯角内,水平极化方式下减缩效果较明显;在-9°~-31°以及1°~37°仰俯角内,垂直极化方式下减缩效果较明显。这主要是因为在这些角度范围内,塞锥的存在有效遮挡了涡轮端壁的镜面反射回波,从而降低了这些方向的RCS。但也存在某些角度由于塞锥与喷管壁面的耦合作用而使得回波加强,如图 7(a)所示的0°~-9°,图 7(b)所示的-32°~-34°,0°附近以及40°附近,喷管M8的RCS大于原始喷管M0。但总体而言,在大多数仰俯角内,加塞锥后喷管的RCS得到了有效的减缩。
4 结论通过本文研究,得到以下结论:
(1) 本文采用物理光学迭代法和等效边缘电磁流法对腔体和棱边的散射特性进行耦合计算。与文献中三角形三面角反射器的实验结果对比验证表明计算方法可靠。
(2) 塞式喷管能够有效降低喷管的雷达散射截面,但在0°仰俯角附近会有局部的升高,在水平极化和垂直极化方式下RCS值分别最大增大8.14%,11.77%;在本文所有塞式喷管算例中,后锥半锥顶角20°的塞式喷管RCS均值减缩效果最好,与原喷管相比,水平和垂直两种极化方式下,在-40°~40°仰俯角范围内RCS算术平均值可分别减小13.2%,15.2%。
| [1] |
张考, 马东立. 军用飞机生存力与隐身设计[M]. 北京: 国防工业出版社, 2002.
(  0) 0) |
| [2] |
杨涛, 杨青真, 李岳峰. 轴对称及二元喷管RCS的数值模拟研究[J]. 航空动力学报, 2011, 26(8): 1819-1823. (  0) 0) |
| [3] |
陈立海, 杨青真, 陈玲玲, 等. 不同喷口修形的二元收敛喷管RCS数值模拟[J]. 航空动力学报, 2012, 27(3): 513-520. (  0) 0) |
| [4] |
高翔, 杨青真, 母鸿瑞, 等. 不同宽高比的二元喷管电磁散射特性数值研究[J]. 推进技术, 2014, 35(6): 735-741. (GAO Xiang, YANG Qing-zhen, MU Hong-rui, et al. Numerical Simulation of Radar Scattering Characteristics for 2-D Nozzles with Different Aspect Ratios[J]. Journal of Propulsion Technology, 2014, 35(6): 735-741.)
(  0) 0) |
| [5] |
CuiJinhui, Shang Shoutang, Yang Qingzhen, et al. Numerical Simulation of RCS for a Spherical Convergent Flap Nozzle with a Non-Rectangular Divergent Duct[C]. Korea: 30th Congress of the International Council of the Aeronautical Sciences, 2016.
(  0) 0) |
| [6] |
杨胜男, 尚守堂, 邵万仁, 等. 球面收敛二元喷管电磁散射特性[J]. 航空动力学报, 2015, 30(12): 2983-2991. (  0) 0) |
| [7] |
郭霄, 杨青真, 施永强, 等. 介质涂覆位置对球面收敛喷管电磁散射特性影响[J]. 航空学报, 2017, 38(4): 1-9. (  0) 0) |
| [8] |
李岳锋, 杨青真, 高翔, 等. 基于迭代物理光学和等效边缘电流方法的S形进气道雷达散射截面研究[J]. 推进技术, 2013, 34(5): 577-582. (LI Yue-feng, YANG Qing-zhen, GAO Xiang, et al. Investigation on Radar Cross-Section of S-Shaped Inlets Using IPO and EEC Method[J]. Journal of Propulsion Technology, 2013, 34(5): 577-582.)
(  0) 0) |
| [9] |
郭霄, 杨青真, 李岳锋, 等. 大宽高比S形二元喷管电磁散射特性研究[J]. 电子设计工程, 2014, 22(12): 13-17. DOI:10.3969/j.issn.1674-6236.2014.12.004 (  0) 0) |
| [10] |
高翔, 施永强, 杨青真, 等. 介质涂覆位置对双S弯排气系统电磁散射特性影响研究[J]. 物理学报, 2015, 64(2): 1-10. (  0) 0) |
| [11] |
Harmon T. System Engineer and Integration Strategy on the X-33 Linear Aerospike Engine[R]. AIAA 97-3317.
(  0) 0) |
| [12] |
Aguilar R. Real Time Simulation of the X-33 Aerospike Engine[R]. AIAA 2001-3562.
(  0) 0) |
| [13] |
Zebbiche T. Supersonic Plug Nozzle Design[R]. AIAA 2005-4490.
(  0) 0) |
| [14] |
Georgiadis N J, DallBello T W, Trefny C J, et al. Aerodynamic Design and Analysis of High Performance Nozzles for Mach 4 Accelerator Vehicles[R]. AIAA 200616.
(  0) 0) |
| [15] |
Hiley P E, Wallace H W, Booz D E. Study of Noz-Axi-symmetric Nozzles Installed in Advanced Fighter Aircraft[R]. AIAA 75-1316.
(  0) 0) |
| [16] |
Ban ken G J, Cornette W M, Gleason K M. Investigation of Infrared Characteristics of Three Generic Nozzle Concepts[R]. AIAA 80-1 1 60.
(  0) 0) |
| [17] |
Chu C W, Der J J, Wun W. A Simple 2D-Nozzle Plume for IR Analysis[R]. AIAA 80-1808.
(  0) 0) |
| [18] |
戴梧叶, 刘宇, 马彬. 塞式喷管三维流场的数值模拟[J]. 北京航空航天大学学报, 2002, 28(5): 601-604. (  0) 0) |
| [19] |
王长辉, 刘宇, 覃粒子. 塞式喷管设计和性能验证[J]. 空气动力学学报, 2008, 26(2): 139-144. (  0) 0) |
| [20] |
陈俊. 涡扇发动机塞式喷管气动与红外辐射特性研究[D]. 南京: 南京航空航天大学, 2011.
(  0) 0) |
| [21] |
Basteiro F, Rodriguez J L, Burkholder R J. An Interactive Physical Optics Approach for Analyzing the Electromagnetic Scattering by Large Open-Ended Cavities[J]. IEEE Transaction on Antennas and Propagation, 1995, 43(4): 356-361. DOI:10.1109/8.376032
(  0) 0) |
| [22] |
Michaeli A. Equivalent Edge Currents for Arbitrary Aspects of Observation[J]. IEEE Transaction on Antennas and Propagation, 1984, 32(3): 252-258. DOI:10.1109/TAP.1984.1143303
(  0) 0) |
| [23] |
Michaeli A. Elimination of Infinities in Equivalent Edge Currents, Part Ⅰ: Fringe Current Components[J]. IEEE Transaction Antennas and Propagation, 1986, 34(7): 912-918. DOI:10.1109/TAP.1986.1143913
(  0) 0) |
| [24] |
汪茂光. 几何绕射理论[M]. 西安: 西北电讯工程学院出版社, 1985.
(  0) 0) |
| [25] |
Polycarpou Anastasis C, Balanis Constantine A, Birtcher Craig R. Radar Cross Section of Trihedral Corner Reflectors Using PO and MEC[J]. Annals of Telecommunications, 1995, 50(5): 510-516.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39


