压气机作为燃气轮机的主要部件,对总体性能有着重要影响。而叶顶间隙造成的泄漏流是内部损失的主要原因之一。在转子正常工作中,磨损,腐蚀,污垢等都会引起叶顶间隙变化,从而影响压气机性能[1, 2]。除此之外,叶顶间隙的泄漏效应会加剧压气机内部流动的非定常特性,导致其下游静子承受较大的周期性载荷,形成周期振动。若此振动频率与静子的固有频率相接近,很有可能引起共振,导致振动幅值较大,可在短时间内引起叶片疲劳甚至损坏。且静子的振动可进一步影响其下游转子的性能参数,所以需要对其进行研究并评估不同情况下的影响。
近年来,大量学者对叶顶间隙相关内容进行研究,主要研究热点集中于叶顶间隙泄漏流在压气机失速过程中的作用,泄漏流诱导产生的轴向及周向压力波的转播,叶顶间隙对压气机性能的影响以及叶顶间隙非定常泄漏诱导产生的叶片振动问题[3, 4]。这些方面并不是相互独立的,而是密切相关的。本文主要对后两个方面进行研究。
关于叶顶间隙对性能的影响。孙海鸥[5],王祥锋等[2]采用商业软件对动叶叶顶间隙变化对压气机性能的影响进行了相关研究。得出叶顶间隙增大时压气机的效率、压比等出现明显的降低,且不同间隙对性能降低程度的影响也不同。杨静[6]等对扭叶片叶栅的叶顶间隙泄漏流进行了数值模拟,得到了类似结论,并解释了损失机理。他们发现随着间隙增大,叶顶泄漏涡与上通道涡的掺混作用使叶片上端区能量损失逐渐增加。此外,很多学者对叶顶间隙的非定常特性也做了相关的研究。杜娟[7]对跨声速轴流压气机非定常机理进行研究,发现随着叶顶间隙增大,发生叶顶泄漏的工况流量也增大,且转子非定常波动触发机理为叶片两侧压差与叶顶泄漏之间的动态循环过程。邓向阳[8]等采用数值方法研究了非定常叶顶间隙流的流动特征和频率特性,指出叶顶泄漏涡的非定常波动为其瞬态空间位置、尺度和形态的周期性变化。吴艳辉[9]采用了实验与数值对比的方法研究了压气机转子叶顶间隙二次流机理,指出二次涡向下游的运动影响了叶顶载荷的分布,从而导致了叶顶出现了周期性的自维持非定常流动,与杜娟结论类似。
对于叶顶间隙诱导引发的激振力及振动响应方面,早期,柴山等[10]对燃气轮机叶片由间隙引起的激振力从理论的角度进行计算分析。王虎,孙爱俊等[11, 12]对于固定静叶尾迹下动叶的振动响应进行研究,介绍并验证了弱耦合振动响应的计算方法。赵书军[13]对固定静叶的压气机中动叶的非定常扰动频率及气动激振力进行分析,得出分离涡、二次涡等为引起非定常激振力的主要原因,且可以根据振动分析得到可能引发共振的工作范围。此外文献[14]对全周动叶表面的非定常激振力进行研究,发现在相对较小的叶顶间隙下,靠近动叶前缘有部分非定常激振力较大。
上述研究大多集中于转子的响应上,且前排都是固定静子或无静子,没有考虑到在轴流压气机中静子的前排也会对静子产生影响,使其振动变形并影响静子尾迹以至于影响后面级流场,导致分析结果的不准确。若能评估在不同情况下静子振动响应的大小,便可根据其结果在压气机后面级的分析中设置静子动网格或对来流添加相应的扰动参数,使结果更加接近真实流场,以提高分析的准确性。所以对静子非定常激振力及振动响应的研究十分有必要。而本文主要对压气机级中转子叶顶间隙这一参数的变化对静子非定常流场、气动激振力以及振动响应的影响进行分析。
2 振动响应方法本节主要介绍由非定常激振力所造成的振动响应的计算方法。本文所采用的方法是解耦方法[15]。利用商业软件NUMECA和ANSYS来计算非定常流动及固体的振动响应。
2.1 方法流程为了研究不同叶顶间隙下的激振力与振动响应,首先要确定CFD网格以及有限元网格(Finite Element,FE)。再利用商业软件NUMECA FINE-TURBO中的约化法对压气机级进行非定常数值模拟,得到三维的非定常流场结果,同时也得到了静子表面的非定常静压分布。然后利用快速傅里叶变换对非定常结果进行频谱分析,将时域结果转变为频域结果,再根据不同频率对应的幅值,将振幅较大的前几阶关键频率和对应载荷进行提取,并利用这些载荷来近似模拟原流场。随后通过CFD-FE插值,得到叶片固体网格表面的载荷,再以谐波的形式加载求解不同阶载荷对应的谐响应结果。最后,利用ANSYS对静子叶片进行模态计算,与上述结果进行对比分析。此外,谐响应方法中涉及到的阻尼包括气动阻尼与结构阻尼,由于本文重点在于叶顶间隙变化的影响,所以根据调研,总的阻尼比可假设为0.02。方法总结如图 1。

|
Fig. 1 Vibration response process under unsteady excitation |
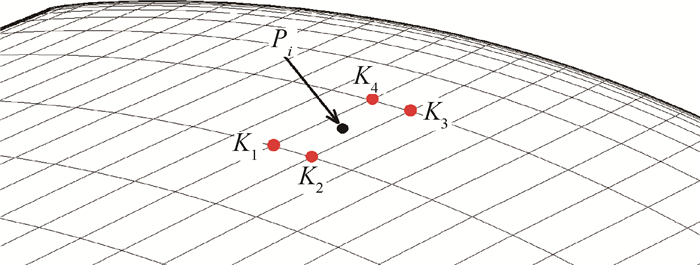
众所周知,由于流体和固体网格的不匹配,通常不能直接将流体网格上的结果加载到固体有限元网格上。所以分阶的非定常静压数据需要通过插值来加载到有限元网格上。本文利用一种简化的径向基函数方法进行插值,如图 2所示,利用带权插值方法进行插值,设距待插值的目标点的距离大小作为插值权重,相距越近权重越大。
|
Fig. 2 Interpolation method |
如图 2,这里Pi为固体网格上待插值点,而图中为其对应在流体网格上的位置,Kj为流体网格上距离Pi最近的几个点。插值函数如式(1),(2)所示。
| $ S = \sum\limits_{j = 0}^n {\left| {{P_i}- {K_j}} \right|} $ | (1) |
| $ D\left( {{P_i}} \right) = \frac{{\sum\limits_{j = 0}^n {\left[{\frac{{S-\left| {{P_i}-{K_j}} \right|}}{S} \times D\left( {{K_j}} \right)} \right]} }}{{\sum\limits_{j = 0}^n {\frac{{S- \left| {{P_i}- {K_j}} \right|}}{S}} }} $ | (2) |
式中D(Pi)是Pi处的数据,|Pi-Kj|为Pi和Kj两点间的距离,且距离越小权重越大。所以,可通过式(1),(2)的计算将流体网格上的数据插值到固体网格上。
2.3 谐响应分析谐响应分析方法主要应用于对连续周期载荷下物体的振动分析,方便设计人员通过振动结果来考虑共振、疲劳和寿命等相关问题。本文中,在流固插值结束之后,预先提取出的前几阶谐波压力载荷便可加载到固体有限元网格上,然后进一步进行谐响应分析。
首先考虑总的结构动力学系统方程式(3)
| $ \left[\mathit{\boldsymbol{M}} \right]\left\{ {\mathit{\boldsymbol{\ddot x}}} \right\} + \left[\mathit{\boldsymbol{C}} \right]\left\{ {\dot x} \right\} + \left[\mathit{\boldsymbol{K}} \right]\left\{ x \right\} = \left\{ {{F_{{\rm{aero}}}}} \right\} $ | (3) |
式中Faero为气动激振力。[M],[C],[K]分别为质量矩阵、阻尼矩阵和刚度矩阵。而非定常激振力可以通过快速傅里叶变化分解成若干阶谐波如式(4)
| $ {F_{{\rm{aero}}}} = \sum\limits_{n = 1}^\infty {{F_n}} \sin \left( {n\mathit{\Omega }t + {\varphi _n}} \right) $ | (4) |
式中φn为对应相位,Ω为分解得到的不同非定常谐波频率,由于转子转动的周期性,Ω一般会受到转子叶片数、转速和其他一些扰动的影响。本文只提取对应振幅较大的前几阶谐波力,然后分别加载到静子叶片表面,进行谐响应分析。
3 数值方法NASA Stage35具有典型压气机级的气动参数及特性,很多研究都以此为对象展开,本文仅对其设计点进行分析,其基本参数见表 1。
|
|
Table 1 Basic design parameter of NASA stage35 |
对于压气机不同叶顶间隙研究,通常在设计叶顶间隙的基础上,还需分别考虑较小和较大叶顶间隙情况。而由公开文献[2, 17],一般在0.5到2倍设计间隙范围变化,可较全面反应叶顶变化的影响。又由于本文以叶顶间隙为单一变量,主要是对机理的研究,等距分布较易于找到随叶顶变化激振力及叶片振动的变化规律[5]。综合考虑本文研究重点及计算资源限制等因素,本文将叶顶间隙按照大小分为4组,以标准叶顶间隙0.408mm为基础,分别取0.5,1,1.5,2倍4组,进行分组计算并对比结果,详见表 2。
|
|
Table 2 Tip-clearance scheme |
本文利用商业软件AutoGrid5划分网格,选择O4H拓扑结构以确定网格质量。由于选择约化法作为非定常计算方法,所以需要对叶片数稍作调整,使静子叶片数为48,这样以来静子的缩略比为46/48=95.8%[1]。而对应的转子静子叶片比为3:4。流道网格如图 3所示。通过网格无关性验证后得到合适的总网格数约为2.4×106,y+=0.9。对NASA stage 35设计点进行计算,所对应的边界条件如表 3所示,其中气体种类为理想气体。

|
Fig. 3 50% span blade-to-blade mesh topology |
|
|
Table 3 Boundary condition |
NUMECA软件提供的湍流模型有Baldwin-Lo max(B-L)模型、Spalart-Allmaras(S-A)模型和各种类型的k-ε模型。S-A模型,是一方程的湍流模型,它可以认为是B-L代数模型和两方程模型之间的桥梁。S-A模型近几年来非常受欢迎,因为它通用性强以及可以处理复杂流动,包含了丰富的经验信息,具有良好的鲁棒性和数值收敛性[18, 19]。与B-L模型相比,它的一个最大的优点就湍流涡粘性场是总是连续的,适合本文中对小涡的周期性分析。与k-ε模型相比它的主要优点是通用性强以及对CPU和内存资源的占用少。所以本文的计算中,雷诺应力的求解采用的是S-A模型。
本文由于主要分析上游转子不同叶顶间隙对下游静子叶片的影响,所以仅对静子进行固体有限元网格划分。如图 4所示,利用商业软件ANSYS APDL进行划分,由于要对三维叶片进行分析,固体结构单元类型选为solid 186,总有限元网格数为1680。而有限元分析对应的三个基本材料参数的设定分别为密度7800 kg/m3,杨氏模量2 × 1011Pa,泊松比0.3。除此之外,静子叶片有限元的边界条件还包括叶片上下表面的无位移约束及面载荷。此处载荷是由流体诱导产生激振力所导致的气动载荷,而如图 4,流体表面有2695个网格点,所以不能直接加载,需利用插值进行加载,插值方法如前文所述。最后再利用AN SYS APDL进行编程,循环加载求解即可。

|
Fig. 4 CFD mesh and FE mesh of stator |
叶顶间隙主要在两个方面对压气机性能有所影响,一是造成流动阻塞,二是间隙的泄漏损失,随着叶顶间隙增大,叶间泄漏增大,和主流掺混,会导致效率及压比下降。由图 5可知,在相同流量的条件下,随着动叶叶顶间隙的增大,效率和压比都有所下降。而在流量为20.65kg/s时,效率与压比分别为0.843和1.789与公开文献[16]中NASA stage35计算结果较吻合,所以计算方法可信。在标准工况下,间隙每增大0.35%弦长,效率和压比分别下降约0.33%和0.28%。和文献中[5]相比较大,主要原因是文献[5]中采取的是3排叶片,总的效率和压比较小,所以下降比例较小。

|
Fig. 5 Pressure ratio and efficiency of 4 tip-clearance |
在非定常计算的基础上,着重对静子表面的气流激振力进行分析。本文中的振动响应主要由周期性气流激振力所引起,所以需要通过压力变化的幅值来进行加载。压力幅值的计算公式如式(5)
| $ p' = \max \left( {\left| {p- \bar p} \right|} \right) $ | (5) |
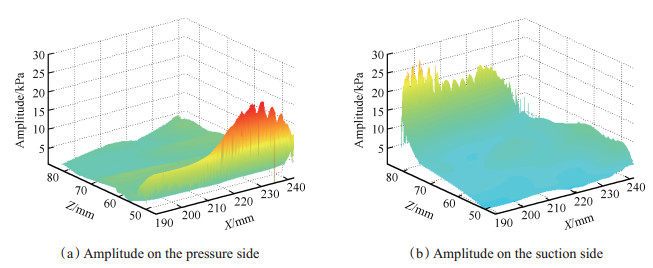
p是时间平均压力,p是随时间变化的压力,p′则为最大振幅。非定常的几种不同的压力幅值分布类似,所以这里仅以方案1为代表分析激振力分布情况,如图 6。
|
Fig. 6 Static pressure distribution of pressure and suction side(scheme 1) |
由图 6(a)可知,叶顶前缘的压力幅值相对较大,尤其在70%叶高处。沿流线方向压力减小,趋于平稳。而对于吸力面压力分布,如图 6(b),总体压力较小,沿着流线方向,在尾缘有较明显上升。
为了分析非定常激振力机理,对于非定常流场,本文取90%叶高的截面进行流场分析。由非定常结果可知,每过40个时间步长,静叶表面有一个新的涡产生并移动到下游尾缘。即计算周期T的1/3,约为96.96μs。而根据转子的转速和叶片数,可以计算出叶片通过频率(BPF),如公式(6)。VR表示转速
| $ {f_{{\rm{BPF}}}} = \frac{{{V_{\rm{R}}}- {N_{{\rm{rotor}}}}}}{{60}} = 10313.2\;{\rm{Hz}} $ | (6) |
通过计算可知低速涡的频率十分接近叶片通过频率,所以可以推断出周期性低速涡是叶片激振力产生的主要原因之一。
以方案1为例,首先给出初始时刻转静相对位置以及转动方向,如图 7所示,叶片从(0/12)T变化到(4/12)T。

|
Fig. 7 Inertial position and rotational direction of rotor and stator |
下面分别从频率和低速涡变化的位置两方面进行分析。图 8显示4个相邻静子叶片在(0/12)T,(1/ 12)T,(2/12)T,(3/12)T,(4/12)T时刻的马赫云图。挑选其中之一观察可知,在(0/12)T时刻,在选中叶片上涡已经开始形成,然后随时间变化,这个涡沿着流线方向移动,并与(1/12)T,(2/12)T渐渐融入前一个大涡,一直到(3/12)T,新的涡在前缘形成。最后到了(4/12)T时刻,又变成了初始时刻,小涡继续形成并加以发展。再结合图 6(a),可发现涡在叶顶前缘成周期性移动,所以在前缘处激振力幅值较大,而叶身及后缘虽有涡的移动,但变化较小,所以激振力幅值较小。

|
Fig. 8 Relative Mach number contour |
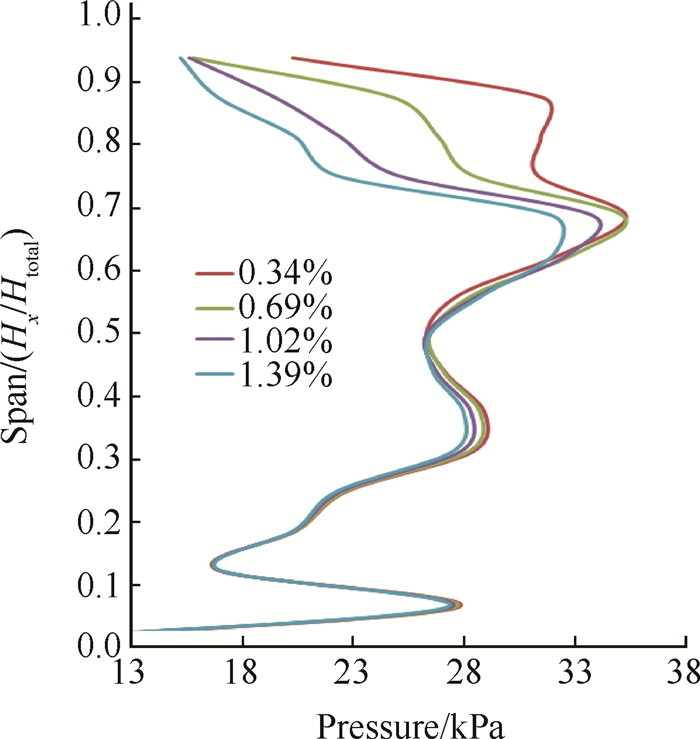
随后对不同叶顶间隙下的激振力进行分析。随着叶顶间隙的增大,叶间泄漏流和主流的掺混会导致流向速度有所降低、压比下降,静子整体激振力会有所减弱,前缘90%叶高处降低较明显。所以在方案1对应的叶顶间隙气流激振力最大。如图 9所示,为叶片前缘时间平均的结果。
|
Fig. 9 Time average pressure distribution of leading edge |
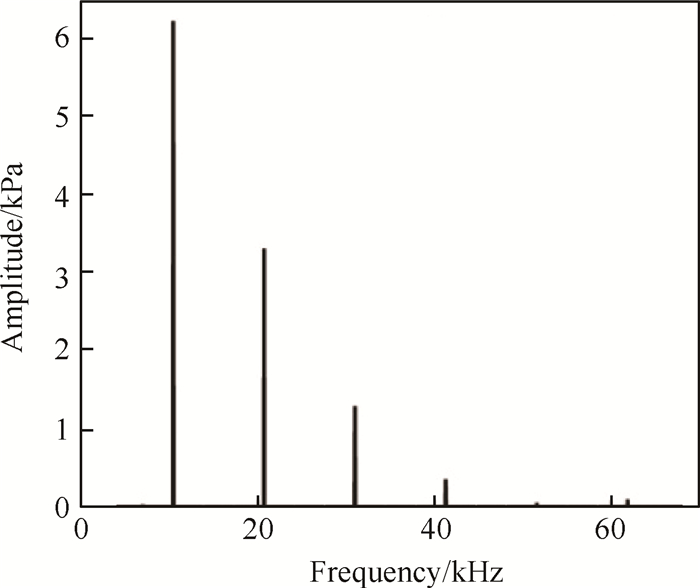
在获得叶片表面压力分布之后,压力波动通过快速傅里叶变换被分解成对应的谐波。初始的时域结果被转化成频域结果,此处选取叶尖前缘的频域振幅图,图 10仅显示了方案1的情况。由图 10可看出压力的波动被分解成若干阶,而其中较为关键的为前3阶,约为10313Hz,20626Hz和30939Hz,约等于叶片通过频率以及其整数倍。而之后若干阶由于振幅约小于第1阶振幅的0.5%,对于静子振动响应几乎没有影响,故此处可以将其后阶舍掉。
|
Fig. 10 Amplitude-frequency features of exciting force |
静子叶片前缘的谐波分量如图 11所示,与图 9相结合,可以发现一阶振幅分布与总分布的趋势较为接近。这就意味着在激振力的压力幅值的分解中,第一阶谐波分量与初始分布最为一致。而相对较后阶的谐波对初始谐波只有较为轻微的扰动。此外,随着叶顶间隙的增大,第1阶压力分布整体幅值也有所减小,而第2,3阶整体只有轻微波动。前文分析可知,由于第1阶压力分量所对应的频率几乎为叶片通过频率,所以激振力的效应最大,而第2阶后叶片间的影响由于时间增大而有明显衰减,导致激振力的减小。随后,这三个气动激振力的谐波会作为固体载荷输入,导入到FE网格上进行谐响应计算。

|
Fig. 11 Pressure distribution of leading edge |
如前文所述,本文主要通过分阶的方式观察静叶的非定常激振力以及激振力所导致的振动响应。使用前文所得的前三阶频率的压力载荷加载到固体叶片上,再通过谐响应方法计算即可。由此可知所对应阶的振动响应也主要跟输入的频率和振幅有关。
图 12展示了不同阶载荷下叶顶间隙变化所对应的叶片前缘沿叶高分布的位移。首先,对于不同叶顶间隙,随着叶顶间隙的增大,位移幅值整体递减,但并非所有位置都成下降趋势,在20%~40%叶高处有非线性现象,位移的波谷有轻微下降。而对于相同阶前缘的位移分布情况基本一致,不同阶会明显的影响到位移分布,说明激振力的频率是影响位移分布的主要原因。随着阶数增大,位移的数值有明显的减小,说明高阶对振动响应的影响较小,主要影响为第一阶振动响应。

|
Fig. 12 Displacement distribution of leading edge |
由于主要分析静叶振动,还对叶片的固有模态进行分析,并与上述结果相对比,如图 13,为第3阶、第8阶和第17阶所对应的模态振型,分别对应着9336Hz,17494Hz和34391Hz。图中叶片前缘的位移分布与图 12相接近,而载入频率和对应模态频率之间较接近但不相等,相差约10%左右,说明在设计过程中需要对接近叶片共振频率的10%域度左右进行分析,以防产生较大振动。而由于振幅的明显变化,其对下游流场计算会有影响,不能忽略,需要在下游分析时使用动网格方法或作为扰动项添加,尤其是间隙较小同时还接近前几阶共振频率时。

|
Fig. 13 Vibration type of blade 3rd, 8th and 17th order |
通过本文的研究,得到主要结论如下:
(1) 随叶顶间隙增大,总压比和效率都随之线性降低,叶片前缘的气流激振力也随之减小,在90%叶高处较明显。由非定常流场细节可知,静叶表面形成周期性低速涡。且叶片前缘涡的变化相对后缘较明显,所以前缘激振力幅值较大。
(2) 由叶片激振力频域结果,主要激振频率为叶片通过频率及其整数倍。分别为10313Hz,20626Hz和30939Hz。且随频率增高,激振力有显著衰减,前3阶尤其第1阶激振力是影响静叶振动的主要因素,与其时间平均结果相近。
(3) 叶片振动响应分析集中于叶片前缘。随着叶顶间隙的增大,位移幅值整体递减,但在20%~ 40%叶高处有非线性现象,位移波谷有轻微下降。第1阶整体振幅值相对第2,3阶较大,且前三阶振动响应结果分别与静叶第3,8,17阶模态振型较为接近,频率相差为10%左右,说明在非共振频率下也可产生明显的振动。
后续对转子流场及振动进行研究,在研究过程中将考虑静子流场中的周期性低速涡和静子变形所造成的扰动,尤其是前一级转子叶顶间隙较小且激振力频率接近静子的固有频率时,以便更加真实准确地反应叶片流场及振动。
| [1] |
Fruth F, VogL D M, MårLensson H, eL al. Influence of' Lhe Blade CounL RaLio on Aerodynamic Forcing ParL Ⅰ: Highly Loaded Transonic Compressor[R]. ASME GT 2010-22756.
(  0) 0) |
| [2] |
王祥锋, 王松涛, 韩万金. 叶顶间隙变化对多级压气机性能影响的数值研究[J]. 科学技术与工程, 2009, 9(12): 3483-3486. DOI:10.3969/j.issn.1671-1815.2009.12.072 (  0) 0) |
| [3] |
Kielb RoberL E, BarLer John W, Thomas Jeffrey P, eL al. Blade ExciLaLion by Aerodynamic InsLabiliLies: a Compressor Blade SLudy[R]. ASME GT 2003-38634.
(  0) 0) |
| [4] |
Thomassin J, Vo H D, MureiLhi N W. Blade Tip Clearance Flow and Compressor NSV: The JeL Core Feedback Theory as Lhe Coupling Mechanism[R]. ASME GT 2007-27286.
(  0) 0) |
| [5] |
孙海鸥, 叶楠, 王纪达, 等. 叶顶间隙对轴流压气机性能及流场的影响[J]. 航空发动机, 2014, 40(3): 1-7. (  0) 0) |
| [6] |
杨静, 杨松. 汽轮机扭叶片叶顶间隙泄漏流动的数值分析[J]. 化工机械, 2016, 43(5): 655-659. (  0) 0) |
| [7] |
杜娟, 林峰, 张宏武, 等. 某跨音速轴流压气机转子叶顶泄漏流的非定常特征[J]. 工程热物理学报, 2009, 30(5): 749-752. (  0) 0) |
| [8] |
邓向阳, 张宏武, 朱俊强, 等. 压气机非定常叶顶间隙流的数值模拟研究[J]. 工程热物理学报, 2006, 27(2): 229-231. (  0) 0) |
| [9] |
吴艳辉, 李清鹏, 田江涛, 等. 轴流压气机转子叶尖二次涡的试验验证及形成机理[J]. 推进技术, 2012, 33(3): 363-370. (WU Yan-hui, LI Qing-peng, TIAN Jiang-Lao, et al. ExperimenLal ValidaLion and Forma-Lion Mechanism Analysis of Tip Secondary VorLex in a Compressor RoLor[J]. Journal of Propulsion Technology, 2012, 33(3): 363-370.)
(  0) 0) |
| [10] |
柴山, 张耀明, 曲庆文, 等. 汽轮机扭叶片级间隙气流激振力分析[J]. 中国电机工程学报, 2001, 21(5): 11-16. (  0) 0) |
| [11] |
王虎, 李琳. 尾流激振下叶片强迫响应数值计算方法[C]. 贵阳: 中国航空学会发动机结构强度振动学术研讨会, 2008.
(  0) 0) |
| [12] |
孙爱俊. 叶轮机叶片在流场中的强迫响应研究[C]. 宜昌: 中国航空学会航空发动机可靠性学术交流会, 2005.
(  0) 0) |
| [13] |
赵书军. 压气机三维非定常流计算与叶片强迫响应研究[D]. 西安: 西北工业大学, 2003.
(  0) 0) |
| [14] |
Fu Z, Wang Y, Jiang X, et al. Tip Clearance EffecLs on Aero-ElasLic SLabiliLy of Axial Compressor Blades[J]. Journal of Engineering for Gas Turbines & Power, 2014, 137(1).
(  0) 0) |
| [15] |
MoffaLL S, He L. On Decoupled and Fully-Coupled MeLhods for Blade Forced Response PredicLion[J]. Journal of Fluids & Structures, 2005, 20(2): 217-234.
(  0) 0) |
| [16] |
薛亮, 韩万金, 黄家骅, 等. 单级压气机气动优化设计[J]. 推进技术, 2009, 30(4): 419-424. (XUE Liang, HAN Wan-jin, HUANG Jia-hua, et al. Aerodynamic OpLimizaLion Design of a Single SLage Compressor[J]. Journal of Propulsion Technology, 2009, 30(4): 419-424.)
(  0) 0) |
| [17] |
张成义, 张宏涛, 冯永志, 等. 叶顶间隙对某型压气机典型级气动性能的影响[J]. 汽轮机技术, 2013, 55(5): 359-360. (  0) 0) |
| [18] |
SpalarL P R, Allmaras S R. A One-EquaLion Turbulence Model for Aerodynamic Flows[J]. La Recherche Aérospatiale, 2003, 439(1): 5-21.
(  0) 0) |
| [19] |
邓向阳. 压气机叶顶间隙流的数值模拟研究[D]. 北京: 中国科学院工程热物理研究所, 2006.
(  0) 0) |
 2018, Vol. 39
2018, Vol. 39

