2017年7月27日是吴仲华先生诞辰100周年的日子。作为一位杰出的科学家，他奠基的叶轮机械两类相对流面三元流动理论为航空发动机的发展做出了巨大的贡献；而他提出的总能系统理论，尤其是“温度对口，梯级利用”的原理在能源的高效清洁利用中也发挥了巨大的作用；他与我国老一辈科学家创立的工程热物理学科，今天已经在航空航天推进、能源利用和环境保护中，发挥着越来越大的作用。作为一位热爱祖国、热爱生活的科学家，他的许多动人事迹，至今仍在广泛传播，成为鼓舞我们不断攀登科学高峰的强大动力。

一 热爱祖国，热爱生活

1947年从著名的MIT取得科学博士（Science Doctor，ScD）后，年轻的吴仲华进入美国国家航空咨询委员会（National Advisory Committee for Aeronautics，NACA，美国国家航空航天局（NASA）的前身）的Lewis实验室（现在的Glenn研究中心）工作。他在给他的两个课题中选择了叶轮机械气体动力学的研究。经过短短的两三年研究，就取得了辉煌的成绩：发表了著名的论文，NACA Report-955和NACA TN-2604，在国际科技界引起了巨大的反响，得到了很高的评价。此时，早就有回国想法的他，到联合国安理会聆听中国代表伍修权控诉美国侵略的发言后义愤填膺，毅然下定决心回国。这以后，他与夫人李敏华先后辞去了在科研单位的工作，到大学教书，并利用移民局星期日休息的机会，巧妙地以旅游为名，绕道欧洲，回到北京，实现了他们投身到新中国的建设事业的愿望。

其实，青年时代的吴仲华就是一个热爱祖国、热爱生活的大学生，他为了抗击日寇的侵略，曾经投笔从戎参加国民党的炮兵部队；但后来看到这个部队不积极抗战，抗击日军的愿望不能实现，他不得不重新回到母校——清华大学。

在昆明，在抗战中的西南联大，他在艰苦的条件下努力学习。也就是在这里认识了与他同岁的李敏华。他们一个人弹钢琴，一个人拉小提琴，一边交流艺术学习的心得，一边沟通人生的感悟，逐渐产生了爱慕之情，最后结为夫妻，成为终生的伴侣。

1943年底，他们双双获得了清华大学的公费留美资格，来到了举世闻名的麻省理工学院，他们刻苦地学习，得到了博士学位：吴仲华在1947年获得科学博士；一年后，夫人李敏华也得到了哲学博士，成为MIT航空系的第一位女博士，在攻读博士期间，他们有了第一个儿子。

二 叶轮机械三元流动理论

二次大战后，各国经济在迅速回升，对新兴的航空工业提出了旺盛的需求。为了飞得更高、更快，必须大大提高航空发动机的性能和可靠性。为此，需要对包含高温、高压、高速、高转速等特点的发动机内部的流动、传热、燃烧等过程开展系统、深入、细致的研究，经常还需要在专门设计的试验台上进行实验。

作为航空发动机核心部件，如风扇、压气机、涡轮等内部流动研究，直到20世纪40年代末期，一直沿用飞机机翼时的孤立叶片模型。这种方法只能计算叶片平均半径处进出口流动参数的变化，不能计算叶片的扭转、弯曲，因为它没有考虑叶片之间的相互作用，对于叶片数量很多的叶轮机械就不适用了。

为了大幅度提高航空发动机和叶轮机械性能，必须针对非常复杂的叶轮机械流动方程组，根据流动的特点，提出简化的物理假定，并创建新的理论模型，在此基础上获得相应的基本方程和求解方法。叶轮机械流动控制方程有^〔2〕

连续方程

$ {\frac{{\partial \rho }}{{\partial t}} + \nabla \cdot \left( {\rho \mathit{\boldsymbol{W}}} \right) = 0} $

(1)

动量方程

$ {\frac{{{\rm{d}}\mathit{\boldsymbol{W}}}}{{{\rm{d}}t}} - {\omega ^2}\mathit{\boldsymbol{r}} + 2\mathit{\boldsymbol{\omega }} \times \mathit{\boldsymbol{W}} = - \frac{1}{\rho }\nabla p + \frac{1}{\rho }\nabla \pi } $

(2)

能量方程

$ \frac{{{\rm{d}}I}}{{{\rm{d}}t}} = \frac{1}{\rho }\frac{{\partial p}}{{\partial t}} + \dot q + \frac{1}{\rho }\nabla \cdot \left( {\pi \mathit{\boldsymbol{W}}} \right) $

(3)

式中ρ为流体密度；p为流体压力；W为流体速度；π为流体粘性应力；${\dot q}$为传热量；ω为叶轮旋转速度；I为相对滞止转子焓，$I = h + {W^2}/2 - {\left( {\omega r} \right)^2}/2$。

这个叶轮机械内部流动的控制方程组是一个非线性程度很高的偏微分方程组，求解难度很大。那时，世界上第一台电子计算机刚问世不久，人们对它的重要意义和巨大潜力还认识不足。年轻的吴仲华利用计算机的强大计算能力，毅然选择了数值求解方法路线，放弃了当时流体力学界普遍推崇的解析求解方法。为此，吴仲华先生也成为从事大规模数值计算的国际领先者之一。

即便如此，由于需要详细考虑三维非定常因素，即使利用当今的计算能力来获得非常满意的数值求解过程也是十分困难的；而且，往往也是不必要的。为此，在理解叶轮机械内部流动特点的基础上，构建相对简化的物理和和数学模型，并能够保持一定数值求解精度，是摆在人们面前必须解决的问题。首先，主要考虑最关注的相对定常流动；其次，粘性流动非常复杂，那时不能作为主要因素来考虑，只能采取与实验数据结合的方法来处理；三维性是当时最关心的，与叶片之间的相互作用密切相关。因此，在定常流动的假定下，着重考虑流动的三维性，兼顾粘性，可能是可行的方法。

在这些假定下，再考虑到在叶轮机械中通常使用熵的梯度来表征流动的损失，上述流动的基本方程组简化为

$ \nabla \cdot \left( {\rho \mathit{\boldsymbol{W}}} \right) = 0 $

(4)

$ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{W}} \times \left( {\nabla \times \mathit{\boldsymbol{V}}} \right) \approx \nabla \rho - T\nabla s} \end{array} $

(5)

$ \begin{array}{*{20}{c}} {\frac{{{\rm{d}}I}}{{{\rm{d}}t}} \approx 0} \end{array} $

(6)

$ \frac{{{\rm{d}}s}}{{{\rm{d}}t}} \ge 0 $

(7)

不难看到，沿流线观察，由于式（3）能量方程中相对滞止转子焓I基本假设不变，导致可以对连续和动量方程进行简化处理，有利于数值求解。但是，即使如此，这组方程在仍然无法利用当时的计算机能力进行数值求解。为此，必须考虑更进一步提出简化模型。

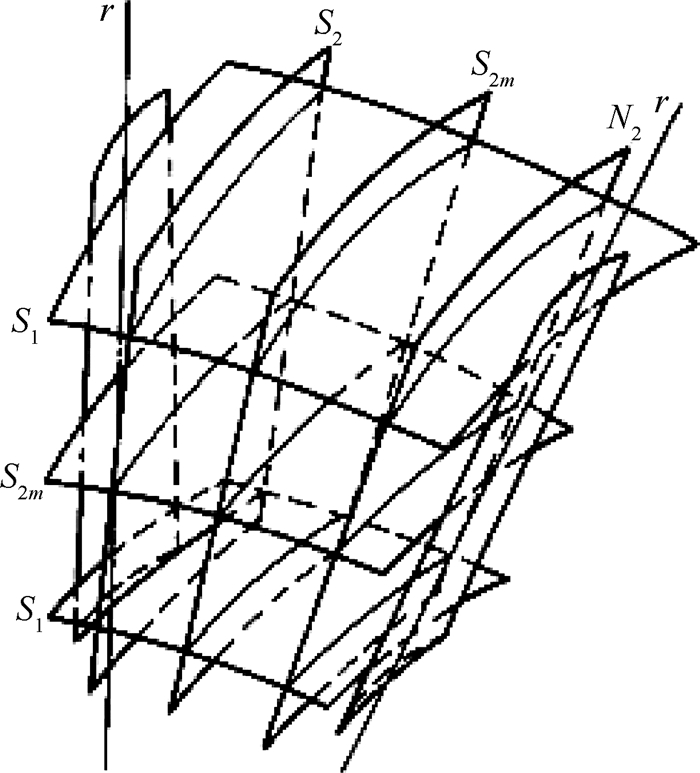
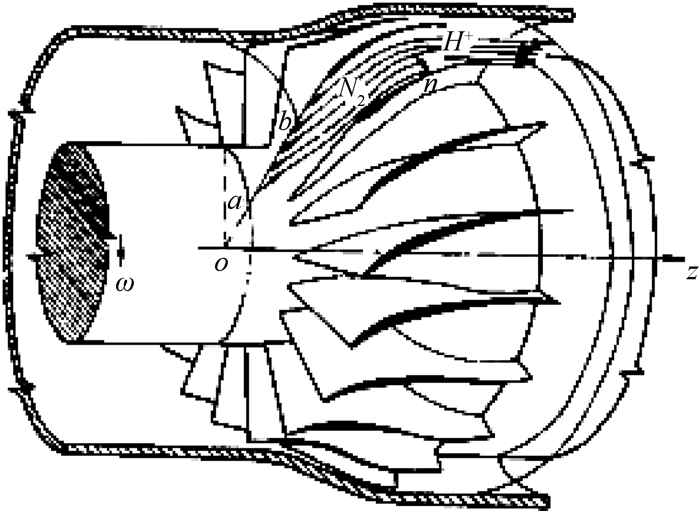
以叶片三维定常流场计算为例来理解吴先生提出的求解思路。可以将复杂的三维流场简化为按不同规律形成的无数条流线和对应流面组成，即将流场、流面和流线三者有机联系在一起。这样通过将复杂三维流动方程转化为一系列流面上的二维流动方程来获得相关流动参数，实现有效降维，从而大大简化了原有复杂三维流场的求解过程。对二维流面上的流动，也无需求解全部方程，而只需选择特定规律下的流面即可。此外，由于二维流面上的流动的相互关联性，可以借助与之交叉流面来进一步简化计算。换言之，复杂叶片之间的三维流动最终可以通过求解相互交叉的S1和S2两类流面方程，突破了原有数值求解难题，详细图解见图 1（叶片间的两类相对流面）和图 2（S2相对流面）。

另一方面，对任意非正交曲线坐标系下的流面:

S（Xⁱ）=0，（i=1，2，3），为构建S1和S2两类流面间耦合关系，可以引入流面偏导数${\bar \partial q/\bar \partial }$，其与空间偏导数$\begin{array}{*{20}{c}} {\partial q/\partial } \end{array}$满足

$ \frac{{\bar \partial q}}{{\bar \partial {x^\alpha }}} = \frac{{\partial q}}{{\partial {x^\alpha }}} - \frac{{{N_\alpha }\sqrt {{g^{33}}} }}{{{N_3}\sqrt {{g^{\alpha \alpha }}} }}\frac{{\partial q}}{{\partial {x^3}}}\;\;\;\;\;\;\;\left( {\alpha = 1, 2} \right) $

(8)

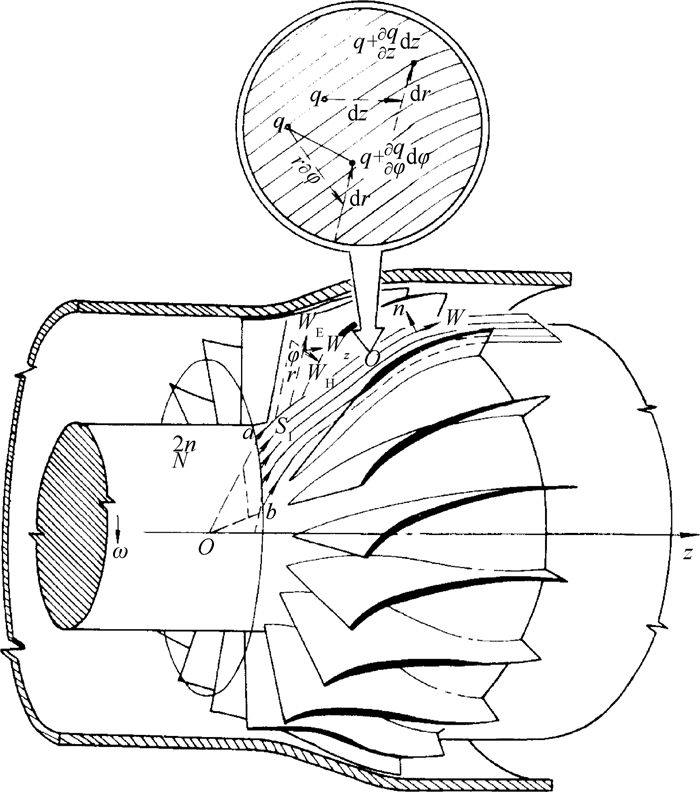
如图 3所示，以方便将空间三维流动基本方程分别转换为流面上对应的二维流动基本方程，即

$ {\nabla \cdot \left( {\rho \mathit{\boldsymbol{W}}} \right) = 0} $

(9)

$ \begin{array}{*{20}{c}} {\frac{{\partial \left( {\sqrt {{g^{ii}}\rho {w^i}} } \right)}}{{\partial {x^i}}} = 0 \Rightarrow \frac{{\bar \partial \left( {b\sqrt g \rho {w^\alpha }} \right)}}{{\bar \partial {x^\alpha }}} = 0} \end{array} $

(10)

在此方程中，除了用流面偏导数代替空间偏导数外，出现了参数b

$ \begin{array}{*{20}{c}} {\frac{{\bar D\left( {{\rm{ln}}b} \right)}}{{\bar Dt}} = \frac{{{n^\alpha }}}{{{n_3}}}\frac{{\partial {w^\alpha }}}{{\partial {x^i}}}} \end{array} $

(11)

从数学上和物理上都可以证明，b代表流片厚度。

X¹方向动量方程

$ \begin{array}{l} \mathit{\boldsymbol{W}} \times \left( {\nabla \times \mathit{\boldsymbol{V}}} \right) \approx \nabla \mathit{\boldsymbol{I}} - T\nabla s \Rightarrow {w^2}\left( {\frac{{\bar \partial {w_2}}}{{\bar \partial {x^1}}} - \frac{{\bar \partial {w_1}}}{{\bar \partial {x^2}}} + 2{\omega ^3}\sqrt g } \right) + \\ {w^3}\left( {\frac{{\bar \partial {w_3}}}{{\bar \partial {x^1}}} - 2{\omega ^2}\sqrt g } \right) + \frac{1}{2}{w_\alpha }{w_\beta }\frac{{\partial {g^{\alpha \beta }}}}{{\partial {x^3}}}\frac{{\bar \partial {x^3}}}{{\bar \partial {x^1}}} = \frac{{\bar \partial \mathit{\boldsymbol{I}}}}{{\bar \partial {x^1}}} - T\frac{{\bar \partial s}}{{\bar \partial {x^1}}} - {F_1} \end{array} $

(12)

由式（12）可见，变量F₁和F₂（见x²方向动量方程）显现，它们为流面间作用力F分量，F可由下式表示

$ \mathit{\boldsymbol{F}} = - \left( {\frac{1}{{{n_\phi }}}\frac{1}{\rho }\frac{1}{r}\frac{{\partial p}}{{\partial \phi }}} \right)\mathit{\boldsymbol{n}} $

(13)

采用三元流动理论，首先要选取合适的两类流面，如图 1所示。即将流道中心面或子午面取作流面，具有明确的物理含义，且以方便计算。其次，需要利用流片厚度b和流面间的作用力F这两个变量联系复杂三维与二维简化流场基本方程之间的关系，同时完成整个计算过程中迭代和收敛程序，最终获得三维流场的简化数值解。

三 工程科学之美的范例

从以上分析可见，复杂的叶轮机械内部三维流场计算被简化为计算两族流面上二维流场，使得整个过程甚至利用当时计算机能力也完全能够实现。对叶轮机械内部流动研究产生巨大贡献：基于该理论和算法，国际上针对叶轮机械内部复杂流动先后开展了相当多深入、系统的基础和关键技术研究，取得了丰硕成果，在此基础上，也大大提高了叶轮机械在效率、可靠性和安全性等性能；基于这一理论和方法，成功地研制出了一代比一代优越的航空发动机和燃气轮机，极大地促进航空事业和能源动力工业的发展。

分析吴仲华先生提出的叶轮机械两类流面理论，可见，流面偏导数类似一座桥梁，实现了叶片空间内三维流场与流面上二维流场之间有机联系，而对应基本方程中反映流动三维特征的流片厚度和流面间作用力成为流面理论模型中最重要的的两大支柱变量。此外，相对滞止转子焓，作为沿流线的相对不变量，也得针对基本方程的求解过程得以极大简化。两类流面理论的精华之处可以概括为一座桥梁、两个支柱和一个不变量。

在这个理论的创建过程中，吴先生将丰富的想象能力、清晰的物理概念、严格的数学演绎和方便的工程应用完美地融合在一起，全方位地体现了工程科学之美。这个基于两类流面的叶轮机械三元流动理论是全面展示工程科学之美的优秀范例。